2次元と3次元の座標変換と回転行列、オイラー角の入り口まで

回転行列への展開：三次元(空間)

一つの座標軸を中心に座標系を回転させる時の回転行列

㉒式の行列 R の各行ベクトルは、上から順に変換後の X₁->Y₁->Z₁ 軸の方向余弦

Z軸廻りのψ回転

まず、Z軸廻りにψ回転させる。

１行目の方向余弦の角度α_０、β_０、γ_０は、定義より変換前のX₀軸、Y₀軸、Z₀軸と変換後のX₁軸のなす角となる（図４)。つまり、

\( \alpha_0=\psi \)、\( \beta_0=\displaystyle\frac{\pi}{2}-\psi \)、\( \gamma_0=\displaystyle\frac{\pi}{2} \)

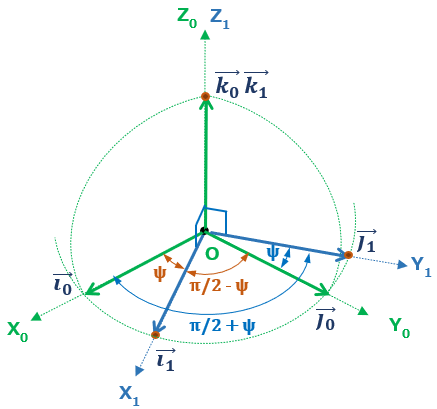
同様に、2行目の行ベクトル（Y₁軸となす角）は

\( \alpha_1=\displaystyle\frac{\pi}{2}+\psi \)、\( \beta_1=\psi \)、\( \gamma_1=\displaystyle\frac{\pi}{2} \)

3行目の行ベクトル（Z₁軸となす角）は、

\( \alpha_2=\displaystyle\frac{\pi}{2} \)、\( \beta_2=\displaystyle\frac{\pi}{2} \)、\( \gamma_2=0 \)

この時の回転行列を R_ψ とすれば

\(\begin{align}
R_\psi &=\small{ \left( \begin{array}{ccc}
\cos\alpha_0 & \cos\beta_0 & cos\gamma_0 \\
\cos\alpha_1 & \cos\beta_1 & cos\gamma_1 \\
\cos\alpha_2 & \cos\beta_2 & cos\gamma_2
\end{array} \right ) }
=\small{ \left( \begin{array}{ccc}
\cos\psi & \cos(\displaystyle\frac{\pi}{2}-\psi ) & cos\displaystyle\frac{\pi}{2} \\
\cos(\displaystyle\frac{\pi}{2}+\psi) & \cos\psi & cos\displaystyle\frac{\pi}{2} \\
\cos\displaystyle\frac{\pi}{2} & \cos\displaystyle\frac{\pi}{2} & cos 0
\end{array} \right )} \\[8pt]
&=\small{ \left( \begin{array}{ccc}
\cos\psi & \sin\psi & 0 \\
-\sin\psi & \cos\psi & 0 \\
0 & 0 & 1
\end{array} \right )} ・・・㉔
\end{align} \)

そのまま続いてY軸廻り、X軸廻り。

Y軸廻りのθ回転

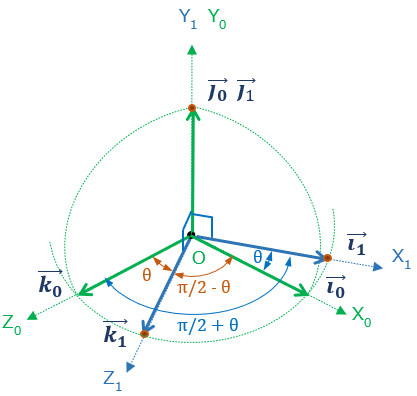
Y軸廻りにθ回転させる回転行列R_θ はR_ψと同様に算出すれば（図5）

\(\begin{align}
R_\theta &= \small{\left( \begin{array}{ccc}
\cos\alpha_0 & \cos\beta_0 & cos\gamma_0 \\
\cos\alpha_1 & \cos\beta_1 & cos\gamma_1 \\
\cos\alpha_2 & \cos\beta_2 & cos\gamma_2
\end{array} \right ) }
= \small{\left( \begin{array}{ccc}
\cos\theta & cos\displaystyle\frac{\pi}{2} & \cos(\displaystyle\frac{\pi}{2}+\theta )\\
\cos\displaystyle\frac{\pi}{2} & cos 0 & \cos\displaystyle\frac{\pi}{2}\\
\cos(\displaystyle\frac{\pi}{2}- \theta) & cos\displaystyle\frac{\pi}{2} & \cos\theta
\end{array} \right ) }\\[8pt]
&=\small{ \left( \begin{array}{ccc}
\cos\theta & 0 & -\sin\theta \\
0 & 1 & 0 \\
\sin\theta & 0 & \cos\theta
\end{array} \right )} ・・・㉕
\end{align} \)

X軸廻りのφ回転

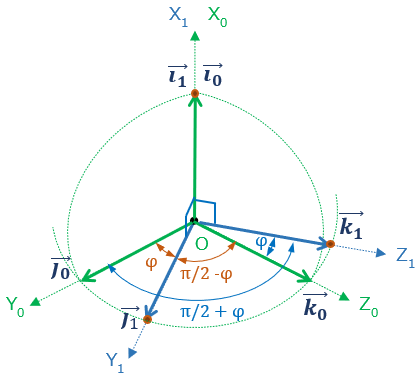
X軸廻りにφ回転させる回転行列R_φ も R_ψ と同様に求めれば（図6）

\(\begin{align}
R_\phi &= \small{\left( \begin{array}{ccc}
\cos\alpha_0 & \cos\beta_0 & cos\gamma_0 \\
\cos\alpha_1 & \cos\beta_1 & cos\gamma_1 \\
\cos\alpha_2 & \cos\beta_2 & cos\gamma_2
\end{array} \right ) }
= \small{\left( \begin{array}{ccc}
cos 0 &\cos\displaystyle\frac{\pi}{2} & \cos\displaystyle\frac{\pi}{2}\\
cos\displaystyle\frac{\pi}{2} &\cos\phi & \cos(\displaystyle\frac{\pi}{2}-\phi )\\
cos\displaystyle\frac{\pi}{2} &\cos(\displaystyle\frac{\pi}{2}+\phi) & \cos\phi
\end{array} \right )} \\[8pt]
&= \small{\left( \begin{array}{ccc}
1 & 0 & 0 \\
0 &\cos\phi & \sin\phi \\
0 & -\sin\phi & \cos\phi
\end{array} \right )} ・・・㉖
\end{align} \)

この㉔、㉕、㉖式が、オイラー角へ続く。

行列 5). オイラー角を使った3次元上の回転変換（ただの回転行列x3）

オイラー角の入り口座標軸各軸まわりにて回転変換を行う行列については以下をご参照。この座標軸廻りの回転行列を使って、3次元上の回転を行うのがオイラー角変換。再度、オイラー角変換は（3次元上の実回転を直接算出する（中心軸まわりに回転する）のでは...