回転行列
次に、変換後の任意の2軸(M軸とN軸)に
”変換前の2軸(X軸Y軸)と同じ原点を共有し、かつ位置関係、直行関係をそのまま保つ”
という制限を加える。
つまり、変換前の座標系を、原点O中心に丸ごと回転させる変換となる。
座標系の設定
変換前の座標軸O-X0Y0は上述と同じ設定。
-> 原点Oを通り、直行するX0Y0軸をもつ座標系。
座標軸は右手系で設定、角度はX→Y方向を正
変換後の座標系をO-X1Y1とし、O-X1Y1も右手系
かつ、”X1軸 Y1軸も直行関係である”、の制限を加える。
つまり、座標系は右手系を保ち軸の配置に変更はしない(角度の正負方向も同じ)
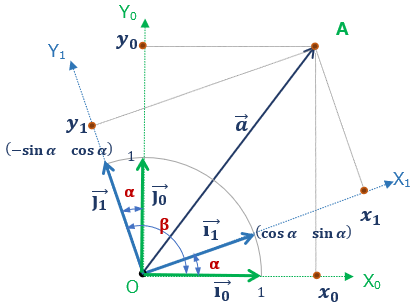
前回同様、平面上に点Aを設定する。
原点Oを始点に点A結ぶベクトルを \( \normalsize{\overrightarrow{a}} \)とし、
O-X0Y0 上の点Aの座標を \( \left ( \begin{array}{c} x_0 \\y_0 \end{array} \right ) \) \( \\[2pt] \) O-X1Y1 上の点Aの座標を\( \left ( \begin{array}{c} x_1 \\y_1 \end{array} \right ) \)
とする(図②)
回転行列の設定と見方
変換される軸は X0軸-> X1軸 、 Y0軸 -> Y1軸 である。
O-X1Y1 ではX1軸Y1軸の関係はO-X0Y0の関係を保つので、αが決まれば、①式のβも自動的にきまる。
つまり
\(\beta= \alpha+\displaystyle\frac{π}{2} \)・・・②
これを前ページの①式に代入すれば
\( \begin{align}
\left ( \begin{array}{c}
x_1\\y_1 \end{array} \right )
& = \left ( \begin{array}{cc}
\cos\alpha & \sin\alpha \\
\cos\beta & \sin\beta \end{array}\right)
\left ( \begin{array}{c}
x_0\\y_0 \end{array}\right) \\[8pt]
&= \left ( \begin{array}{cc}
\cos\alpha & \sin\alpha \\
\cos(\alpha+\displaystyle\frac{π}{2}) & \sin(\alpha+\displaystyle\frac{π}{2}) \end{array}\right)
\left ( \begin{array}{c}
x_0\\y_0 \end{array}\right) \\[8pt]
& = \left ( \begin{array}{cc}
\cos\alpha & \sin\alpha \\
-\sin\alpha & \cos\alpha \end{array}\right)
\left ( \begin{array}{c}
x_0\\y_0 \end{array}\right) ・・・③
\end{align} \)
これが回転行列。
(当然ではあるが、一つの回転角αで変換前後の座標値の関係を示す事ができる)
この行列の見方は軸変換の場合と同じである。
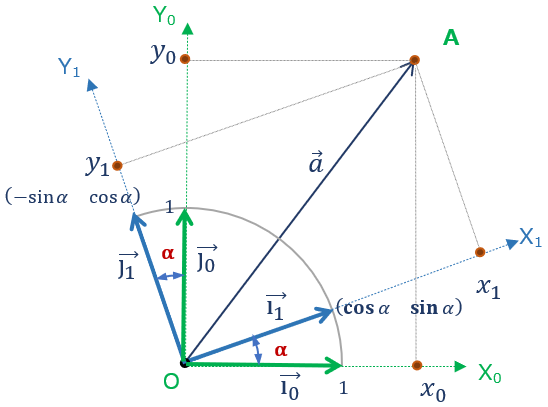
Ra において、1行目を抜き出した \( (\cos\alpha \sin\alpha) \) を \(\overrightarrow{i_1} \)、2行目を抜き出した \( (-\sin\alpha \cos\alpha) \) を \(\overrightarrow{j_1} \)とみれば、これらの行ベクトルは変換後の軸の方向である。
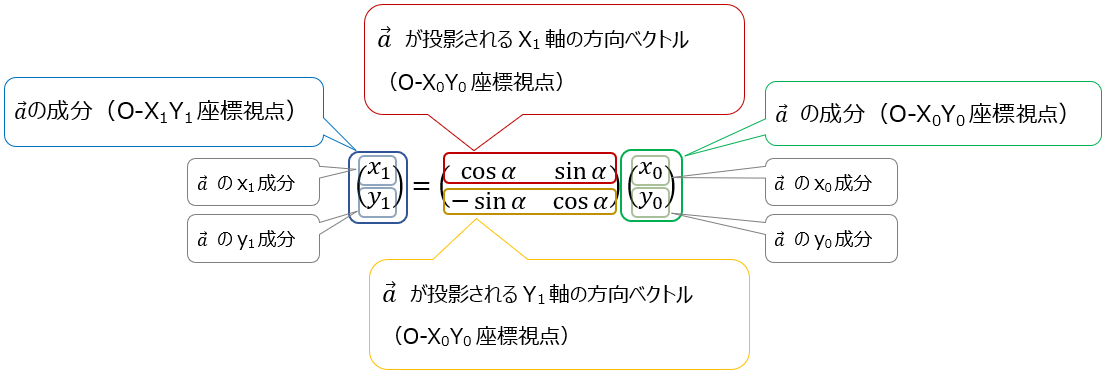
つまり、行列内の各行ベクトルは変換後の軸の方向を示す。
また回転しただけなので当然\(\overrightarrow{i_1} \)、\(\overrightarrow{j_1} \)もその平面上での正規直行基底(大きさ1&互いに直行)
追記
ベクトルの内積を用いた軸変換から回転行列へと展開したが、回転行列については、方向余弦を用いた導入の方がわかりやすいかも。。以下の記事にて。

