各ベクトルの大きさ
さて成分計算。図1から力のつり合いを追いかけて算出するのが簡単。
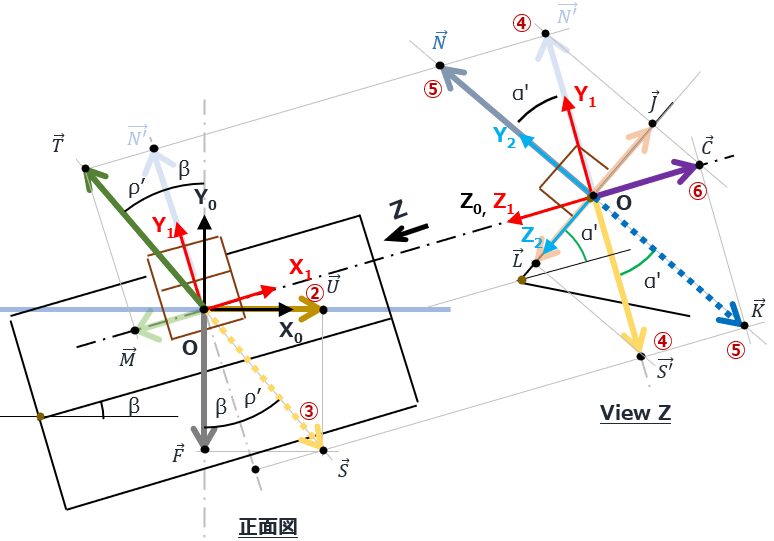
まず、\( \tt \vec{S} \)の大きさから、、
\( \tt |\vec{S} |= \displaystyle \frac {\tt |\vec{F} |}{\cos( {\beta+\rho’}) } \) ・・・③
これを使えば、\( \tt \vec{S}’、\vec{N}’ \) の大きさは
\( \tt |\vec{S}’ |= |\vec{N}’|= |\vec{S} | \cos{\rho’} =\displaystyle \frac {\tt |\vec{F} | \cos{\rho’} }{\cos( {\beta+\rho’}) } \) ・・・④
ここから、\( \tt \vec{K}、\vec{N} \)の大きさは
\( \tt |\vec{K} | = |\vec{N}| = \displaystyle \frac {|\vec{S}’ |}{\cos{\alpha}’} = \displaystyle \frac {\tt |\vec{F} | \cos{\rho’}}{\cos( {\beta+\rho’}) \cos{\alpha}’ } \) ・・・⑤
と求まる。
(ついでに、 \( \tt |\vec{C} | = \tt |\vec{S}’| \tan{\alpha}’= \displaystyle \frac {\tt |\vec{F}| \cos{\rho’}\tan{\alpha}’ }{\cos( {\beta+\rho’}) } \) ・・・⑥ )
さて⑤式と、②-1&②-2式の \( \tt |\vec{M} |= |\vec{N}’ |\tan{\rho}’ = N\tan{\rho} \)を使えば、
\( \tt \tan{\rho}’ =\displaystyle \frac {N\tan{\rho}}{N’} = \frac {\tan{\rho}}{\cos{\alpha}’} \) ・・・⑦
が求まる。
斜面の定理のねじ面への展開
さて、②式の再登場させる
\( \tt |\vec{U}| =\tt |\vec{F}| \tan({\beta+\rho’}) ・・・② \)
β角の小さいねじ面を前提として近似を使って式を簡易化していく。先に書けば、近似結果はこうなる
\( \tt |\vec{U}| ≒ \tt|\vec{F}| (\tan{\beta} + \displaystyle \frac {\tan{\rho}}{\cos{\alpha}} ) \)・・・⑧
-> ②式から⑧式に至る過程で⑦式を使うが、ちょっとわかりにくいので詳細は次章 補足にて。一旦結論まで。
この⑧式にねじの諸元を当てはめる。
\(\tt |\vec{U}|=U、\tt |\vec{F}|=F_s、\tan{\beta} =\frac {P}{\pi d_p}、\mu_s =\tan{\rho} \) を使えば冒頭の⓪式が求まり、
\( \tt U = F_s \cdot (\displaystyle \frac {P}{\pi d_p}+ \displaystyle \frac {\mu_s}{\cos {\alpha}}) \)
緩め側も含めれば、
\( \tt U = F_s \cdot (\displaystyle \frac {{\pm}P}{\pi d_p}+ \displaystyle \frac {\mu_s}{\cos {\alpha}}) \)
これにねじ面の有効半径 \( \tt \frac {d_p }{2} \) をかけてやれば、ねじ面に作用するトルクTsと発生する軸力の関係が求まる。
以下である。
\( \tt T_s = \displaystyle \frac {F_s }{2} \cdot (\displaystyle \frac {{\pm}P}{\pi}+ \displaystyle \frac {\mu_s \cdot d_p}{cos {\alpha}}) \)
これに座面に作用するトルクTwを足し合わせれば、入力するトルクTfと軸力の関係式が求まる。
詳細は先の記事にて。
補足:近似による誤差
補足にて、⑧式の導入に使われる近似について確認。
というのも、”ねじ締結概論”では\( \beta\)が小さい事から、\( \rho’\)=\( \rho \)、\( \alpha’\)=\( \alpha \) を近似的に(近似”的”って?ん?)、また”ねじ締結の原理と設計”では近似が含まれる \( \tt \frac {1}{\cos{\alpha}’}\)を、”=1.155″ と定数化してあったり(ん?)で、その近似の詳細は省略??、、、で、ん?ん?と。。。
で、気づいた。ん?の原因は、ねじ面を前提として近似が使われている事が頭の中から抜けていたせい。。。
まず、②式から⑧式への計算の流れ(近似込み)は
\(
\begin{align}\tt |\vec{U}| &= \tt |\vec{F}| \tan({\beta+\rho’}) ≒\tt |\vec{F}| (\tan{\beta}+\tan{\rho’}) \\[8pt]
&= \tt |\vec{F}| (\tan{\beta}+\displaystyle \frac {\tan{\rho}}{\cos{\alpha}’} )≒\tt |\vec{F}| (\tan{\beta}+\displaystyle \frac {\tan{\rho}}{\cos{\alpha}} )\\[8pt]
\end{align}
\)
これが大枠の流れ。
さて最初の近似、この部分から確認
\( \tt |\vec{U}| = \tt |\vec{F}| \tan({\beta+\rho’}) ≒\tt |\vec{F}| (\tan{\beta}+\tan{\rho’})\)
ん、大胆すぎない?とも思ったが、tanの加法定理の近似を図示すれば
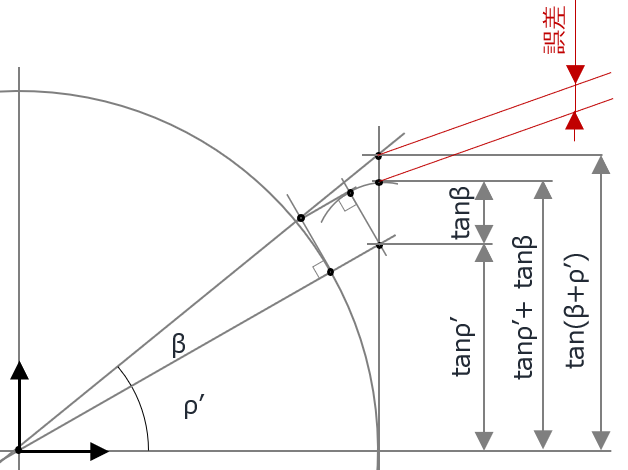
この近似は”βが小さい”&”ρ’が小さい”程 近似の精度は上がる。これが参考書に書いてある”βが小さい”の意味。
念のため、近似のレベル確認。
ねじ面である事を踏まえよく使う範囲として、摩擦係数μ(tanρ)は大体0.2-0.3ぐらい、βは大体3°(tanβでいえば0.05)ぐらいを想定して計算してみると、
誤差はだいたい1.5%ぐらい発生(大体の目安)
ちなみに摩擦係数μの最大を0.5、βを最大4°(tanβ=0.08)で計算すると、最大誤差は4%程度ぐらいで発生(こちらも目安)。<- 以下の表、誤差Maxが3.67 %
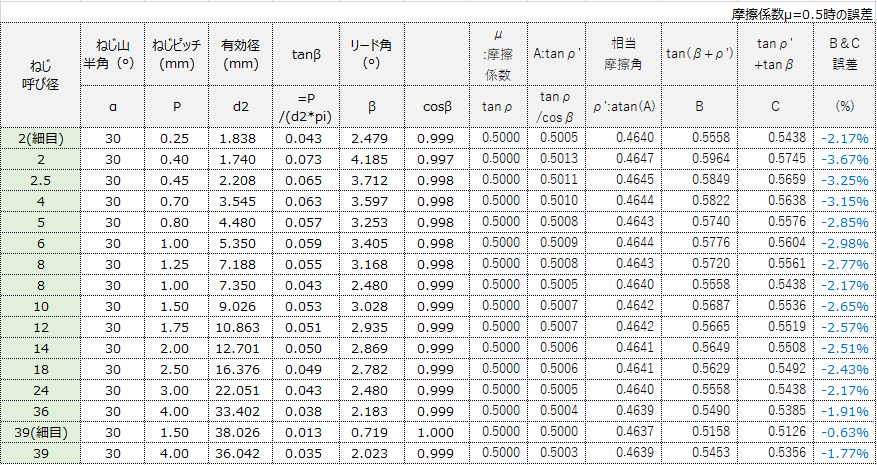
近似式とするには誤差が結構大きい気もするが、摩擦係数(tanρ)自体のバラつきが±30%ある事も踏まえれば、まぁ、実用範囲内かと。(参考書にも、近似式と書かずに近似”的”って書いているし。。)
さて、計算を続ける。⑨式に⑦式を代入して
\( \tt |\vec{U}| ≒\tt |\vec{F}| (\tan{\beta}+\tan{\rho’}) =\tt |\vec{F}| (\tan{\beta}+\displaystyle \frac {\tan{\rho}}{\cos{\alpha}’} ) \)
ここから二つ目の近似部分。
\(
\begin{align}\tt |\vec{U}|
&≒\tt |\vec{F}| (\tan{\beta}+\displaystyle \frac {\tan{\rho}}{\cos{\alpha}’} )\\[8pt]
&≒\tt |\vec{F}| (\tan{\beta}+\displaystyle \frac {\tan{\rho}}{\cos{\alpha}} )・・・⑧
\end{align}
\)
これには、①式の \( \tan{\alpha’}= \tan{\alpha} \cos {\beta} \) の関係を使う。ねじを前提とすれば斜面の勾配角βはねじのリード角に該当し、これは最大でも5°以下。
このβを踏まえ、\( \cos {\beta}≒1 \) として、①式は\( \tan{\alpha’}≒ \tan{\alpha} \)と近似。ここから\( \cos{\alpha’}≒ \cos{\alpha} \)。
念のため、ねじ諸元ベースで確認してみるとこの誤差は0.1%未満(以下の表 cosα’/cosα 参照)。
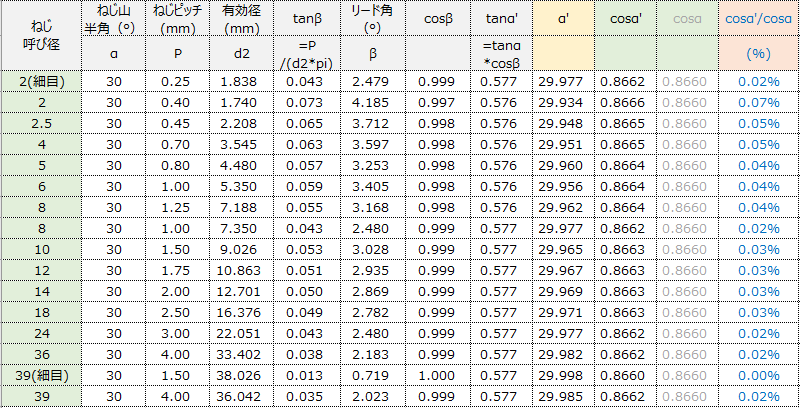
こちらは各ねじ諸元値の有効桁から言っても、近似式としてよいレベル(誤差:1/1000以下)
よって、⑧式にたどり着く。
蛇足ではあるが、近似を使わないのであれば、
\(
\begin{align}
\tt |\vec{U}|
&=\tt |\vec{F}| \tan({\beta+\rho’})=\tt |\vec{F}| \displaystyle \frac{\tan{\beta}+\tan {\rho}’}{1-\tan{\beta}\tan {\rho}’}\\[8pt]
&=\tt |\vec{F}| \displaystyle \frac{\tan{\beta}+\frac {\tan{\rho}}{\cos{\alpha}’}}{1-\tan{\beta}\frac {\tan{\rho}}{\cos{\alpha}’}}\\[8pt]
&=\tt |\vec{F}| \displaystyle \frac{\tan{\beta}+\frac {\tan{\rho}}{\cos({tan^{-1}(\tan{\alpha}\cos{\beta}}))}}{1-\frac {\tan{\beta}\tan{\rho}}{\cos({tan^{-1}(\tan{\alpha}\cos{\beta}}))}}
\end{align}
\)
となる。(ちょっとおあそび)
確かに理論式でこの先展開をしていくには、これではちょっと面倒。もともとバラつきの大きいモノ(摩擦係数)が含まれているしで、机上の不要な精度追及になりかねないっていうのもあるのかな。。。

