1=0.9999・・・が感覚的にすっと理解できなかったけど
この式、違う値にみえるのに等式で結んでいることが、感覚的にずっとすっきりせんかった。(違和感ありあり)
理屈は
1/3 =0.333・・・より、
1= 1/3 x 3
=(0.333・・・) x 3= 0.9999・・・よって 1=0.9999・・・
もしくは
x=0.999・・・とおくと 10x=9.99・・・
この2式を左辺同士、右辺同士をひき算して10x-x=(9.999・・・) – (0.999・・・)=9 から
9x=9 より x=1もとは x=0.999・・・より 1=0.999・・・
とか聞けばわかる。わかるんだけど、、頭の芯が納得できていていない感覚が長かった。。
で、少しはすっきり感をもたらすための覚書
実数を離散系で(デジタル的に)考えない
改めて考えてみた。数字を見るときにどうしてもデジタル的というか、自然数的にみてしまう事が原因
(数字を離散系でとらえている)。
同じじゃないという感覚は、きっとここからきている。つまり、
- 1と0は当然同じではない
-> 1 ≠ 0 - 数直線の解像度を一桁あげて、1.0 に一番近い値 0.9 と比較しても、1.0 と同じにはならない
(解像度:1/10、最小単位:0.1)
->1 .0 ≠ 0.9 - 解像度をもう一桁あげてみても、一番近い0.99は1.00と同じではない
(解像度:1/100、最小単位:0.01)
-> 1.00 ≠ 0.99
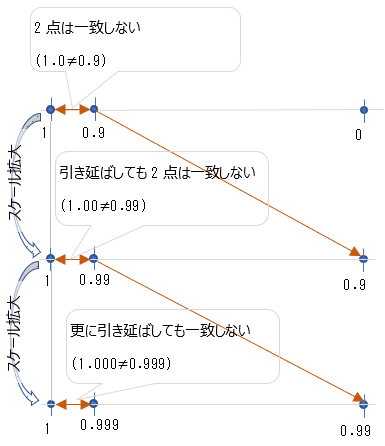
当たり前だが、このまま解像度を上げていっても、この考え方の延長には”≠” が “=” に切り替わる点はないが、なぜか最後は”=”になる。
-> 1=0.9999・・・・にはたどり着かない
つまり勝手に実数を ”有限な解像度” でみてしまっていることが問題。
実数は連続系(アナログ的)。見方を変える
そもそも(大前提の)実数の連続性を忘れている。
つまり、0.9999・・・の ”・・・” (極限を示す記号)の意味をすっとぱしている。
実数であるという事は、 ”0.999・・・” は、”切れる事が無くつながっているが故に限定できない事”(アナログ信号的)をしめしている。
-> 無限に拡大しても必ず該当する値が存在し、かつ隣の値と切れ目なく滑らかにつながっている。
つまり、数字を段付きで変化するデジタル的(離散系)な考えでは、アナログ的(連続系で)な解答を求めるお題に対しては、答えにたどり着かない(すっきり感は生まれない)。
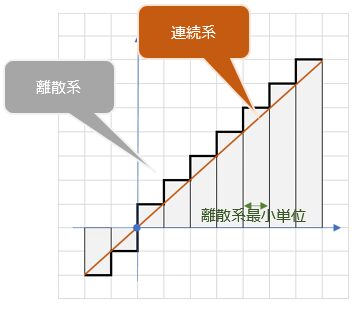
(連続系:直線(オレンジ)、離散系:階段線(黒))
例えて言うなら、どれだけ小さなレゴブロックで坂道を作っても、滑らかな坂道にはならないのを知っているのに、一生懸命レゴブロックを小さくして滑らかな直線をしようと頑張っている感じ。
→ 極限の世界へ
連続系で(アナログ的に)再度考える:
1を1.000・・・ と書き直す
連続性についてはこちらにも
さて、ざっくりと”連続”とは点と点が切れ目なくつながっているという事。
”切れ目がない” とは、ある値”A”に対して、Aより大きい値から近づいてもAより小さい値から近づいても、同じ値”A”にむかって切れ目なく近づける。
(ちなみに、別の点に行きつくのであればそれは切れ目、その数直線は ”連続ではない” )
さて再度詳細に、左辺の1の解像度を無限大にしてみる。
つまり、1=1.000・・・とすれば、1=0.9999・・・ は、
1.000・・・ = 0.999・・・
(1.000・・も0.999・・ともに小数点以下は無限に続くと考える(実数表記)。)
この形で見れば、
- 左辺( 1.000・・・ )は大きい方から1に近づく数字の様子
- 右辺(0.999 ・・・ )は小さい方から1に近づく数字の様子
と見ればよい 。
これは ”極限においては、この両辺は等しいところに落ちていく” 事を示していると理解すれば、なんとなくすっきりする。
つまり、極限では同じ点に行きつき重なっていく(一致していく)= 連続しているの意味にて、これが、
”実数は個々の存在そのものに連続性という極限概念がある”
の意味。無理数は当然として、有理数(整数、分数)も、実数の世界では無限小数。整数のようなきりの良い数字はない。
(数直線を切れば、切りのいい数字に確定はできるが、連続性はなくなる。)
ある意味、実数の世界を表現するのに無限小数の世界が必須である事が、値が極限でもつながっている事、つまり連続性(アナログの世界)を示唆している と考えておけばよい。
(デジタルの様に数字が階段上に変化したのでは、数字の連続性は保てない(切れ目ができている))
無限小数への抵抗感はなくしておこう
この感覚のベースは、無限小数への抵抗感がなくしてしまえば、あまり不思議に感じなくなってくる。
実数の世界ではそもそもすべての値が無限小数で表される事が当たり前。。と思っておけばよい。
実数の世界からみれば、慣れ親しんでいる1とか2.5とか切りの良い整数、小数、分数(つまり有理数)の方が特殊で、簡易表記が可能な数字は少数派。(無理数の簡易表記もほんの一部(πとかeとか)あるが。。)
こうしてみると、お題は、
”実数が連続している” の意味を感覚的に捉えらえてしまえば、不思議に思わなくなる。
有理数、無理数については以下、同じ観点
連続性について、より正確な(数学的な)捉え方(入り口)は、以下の本がおススメ。読み物としても面白い。
追記
ちなみに、デジタル信号(離散系)で動く機器(電卓とか)では、極限が弱点なのはよく知られている
(電卓も計算誤差が発生する)。要は連続性が保てない。。
(例えば、(1÷3) x 3 = 0.999 となる電卓は存在するし、電卓で1/3=0.3333・・を確定させると、それ以降の同一内計算では解像度による誤差が発生するため”=”は成立しない。)
まぁ、実用上困らないが、このあたりが取り込めると(極限への理解)、数字の世界でのひっかかりがちょいと減った記憶があったので覚書化


