実数の世界は、有理数と無理数で成り立つ
実数は”個々の存在そのものに連続性という極限概念がある”、、なんて聞くと何だ?? となるが、簡単にいえは、
- ”数字は切れ目なく連続して繋がっている”
という事。
以下が実数の連続性の意味
ちなみに、実数は有理数&無理数からなっており、、
- 無理数は無理な数じゃなくて、”理数が無い数”(無・理数)。
- 有理数は”理数が有る数”(有・理数)
実数の世界は、”理数”のあり/なしの二つで分類されている。
じゃぁ、理数って何だ?で、覚書
有理数と無理数は比で表現できるかどうか
で、有理数は Rational Number の訳。 つまり比(Ratio)で表現できる数。
で、ここでの比とは、
- ベースとなる値 \( a \) に対するある値 \( b \) の比の事。
つまり \( \dfrac{b}{a} \) であらわす事ができる数(\( a \) , \( b \) は整数で互いに素、\( a≠0 \) )。
なんだ、有理数ってざっくりいうと、分数って事かい。
ちなみに、\(a=1\) の場合は整数。
で、反対に、無理数は 比(分数)で表現できない数
(Ir-rational number)。
(有比数 & 無比数とかで訳しておけばいいのに。。。)
例えば、平方根とかπとかeとか
つまり ”有理数、無理数の区別は、分数の形で表すことができるかどうか”だけ
(もちろん整数を使った分数)。
まとめれば、
- 有理数
:分数で表現できる数(Rational Number) - 無理数
:分数で表現できない数(Irrational number)
実数起点で分類すると(分数観点)
図でかけばこんな感じ
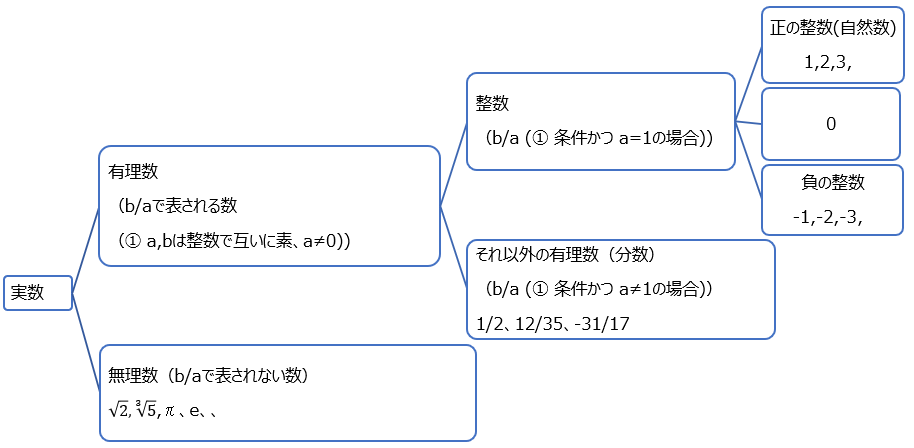
無理数は実数からみると多数派
さて、有理数は実数全体からすると、分数であらわされる数字でなければならないので、特殊な性質をもった数字のグループ
ある意味特殊部隊。無理数枠に入る数字の方が主流派。
実数はすべて無限小数としておく
整数も含め有理数も、全部無限小数とみる(有理数、無理数かかわらず、実数はすべて連続であるの極限概念を持つことから)
例えば、”1”はたまたま”1”と表記できるだけであって、
ホントは1.000・・・である と。
としてしまえば、
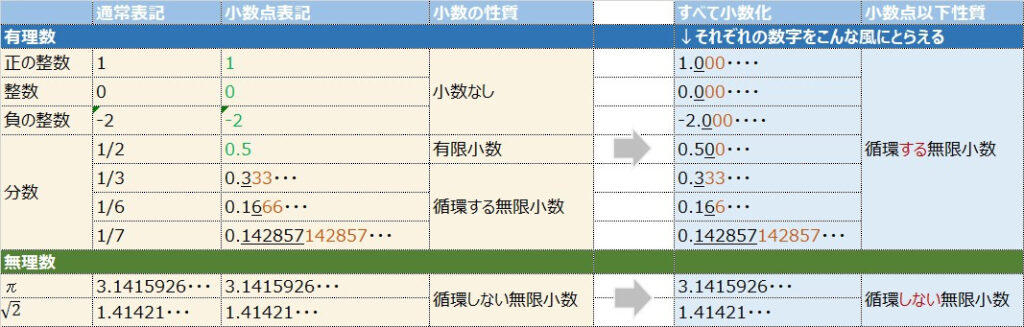
- 実数は全て無限小数
- 有理数:循環する無限小数
- 無理数:循環しない無限小数
の基準のみ
再度、実数起点で分類(無限小数観点)
有理数と無理数の違い
まとめなおせば、以下。
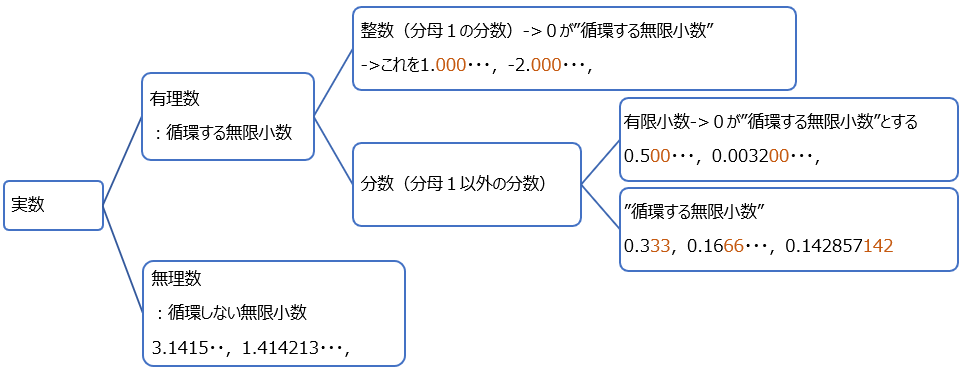
再度
- 有理数は全て”循環する無限小数” :(何桁かの)同じ数字が無限に繰り返す
- 無理数は全て”循環しない無限小数:不規則な数字が無限に続く
-> 小数が循環すると有理数、循環しないと無理数
この有理数/無理数に区別がない事が、実数すべてに ”連続性という極限概念がある” 事への理解の手助けとなるかと。
実数の世界
再度、実数は ”連続性という極限概念を持つ” とは、
”実数軸上の点の集合(数直線)であり、切れ目なくつながっている連続した点の集合”
ということ。
連続性を持つことから、実数としての点は一点のみ存在するが、値を表すとき小数点は無限に続く数字というのが本来の姿。
一見、整数のように切りのいい数字に見えても、実数の世界では、小数点以下に0が無限に続いている(1 -> 1.000・・・)。
← 切りがよく見えるのは、この小数点以下の0を省略している過ぎない。
加えて、有理数だけでは実数の世界は成り立たない(連続性)。無理数が加わってはじめて実数の世界が成り立ち、隙間のない実数の連続性を保たせている。
この感覚が普通になってくると、1=0.999・・・と聞いても違和感がなくなってくる
追記
無理数は、毎度、一匹狼的に特殊な有用な数字と個別に導入されるから、かなりとっつきにくい。
(平方根とか円周率πとか自然対数のネイピア数eとかとか)。
目にするのは有益な無理数にのみで、これらに記号が与えられている(πとかeとかルート記号(√)等々)。
無限小数は、整数/分数の様に簡略表現できないので、一つの記号で表示できるようにしている。(1とか1/2とか書いているのと差はない。)
目にする無理数は個別(特別)扱いされている事もあって、わかりやすい整数 → 有理数から入ると印象悪し。。ただ、正確に表記できない無理数は無限に存在。。。

