はじめに
前回までは、一次元での慣性力(加速減速)、二次元での慣性力 (遠心力)の覚書
今回は三次元での慣性力、ジャイロ効果。その仕組みを以下に。。。
ジャイロ効果って? 三次元で発生する慣性力
ジャイロ効果は、とっつきにくい。
一例としては、高速で回転しているモータを手にもって、傾けようとした時に感じる変な抵抗感がそれ。意図した方向に物体が傾かないが故に、傾ける事自体に物体が抵抗しているような感覚/違和感をもってしまう。
この回転体の中心軸を傾ける時に発生する動きの様をジャイロ効果と呼び、その時の発生モーメントをジャイロモーメントという。
遠心力と違って日常での体験は認識しづらいが、こういうので気軽に体感できたりする。意外とその力の大きさにびっくりする。
さて、回転体上の質点からすれば、ジャイロモーメントも遠心力と同じ慣性力を起因とする(見せかけの力)。
結局ジャイロモーメントも遠心力と同じ仕組み、つまり、ニュートンの運動の第一法則
”外部から力を加えられない限り、静止している物体は静止状態を続け、運動している物体はそのまま動き続ける”
が根っこ。これが示唆する”慣性”に行きつく
遠心力は2次元で発生する慣性でわかりやすいが、ジャイロモーメントは3次元でとらえる必要があるので少しややこしい。
ただ発生している仕組みがわかれば”なんだそれだけかい!”って感じにはなる。。。
ジャイロモーメントが発生する状況
ジャイロモーメントは回転体を傾けている間のみ発生
まず、ジャイロモーメントが発生する状況は、
- 回転体の中心軸を傾斜させたとき
(回転する剛体の中心軸を傾斜させるモーメントを与えたとき)
これだけ。
ジャイロモーメントは傾斜と同時に発生し、その発生面は
- ”中心軸の傾斜面に直角”かつ ”その中心軸を通る面”
座標軸を使えば、例えばXYZ座標軸を右手系で設定、Z軸を回転体の中心軸(回転軸)にとり、このZ軸をY軸廻りに傾斜させれば、
- ジャイロモーメントは、X軸廻りに発生する
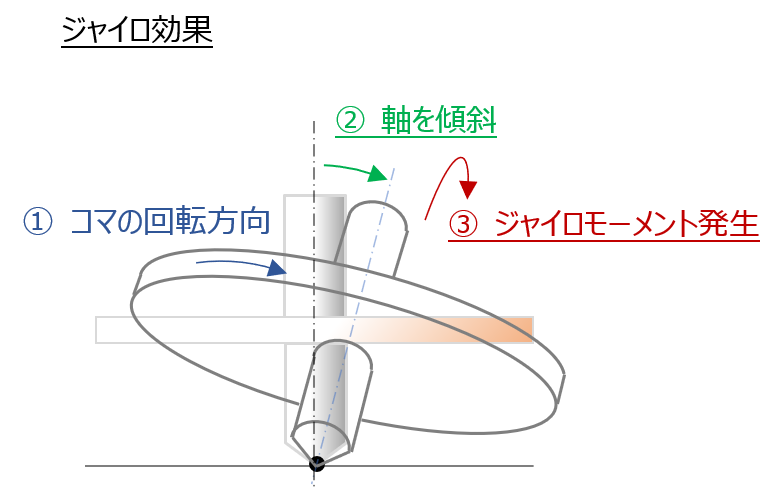
つまり中心軸は
- 意図して与えたモーメントによる傾斜(Y軸まわり)
- 発生するジャイロモーメント”による傾斜(X軸まわり)
の二つのモーメントを足し合わせた傾斜方向に傾く。
逆に言えば、回転体の中心軸に一定方向の傾き(Y軸まわり)を与えても、その意図した方向には傾かない事を意味する(これは、実感通り)。。
ジャイロモーメントの発生する仕組み
以下は、このジャイロ効果が発生する仕組み。
回転体モデルの設定
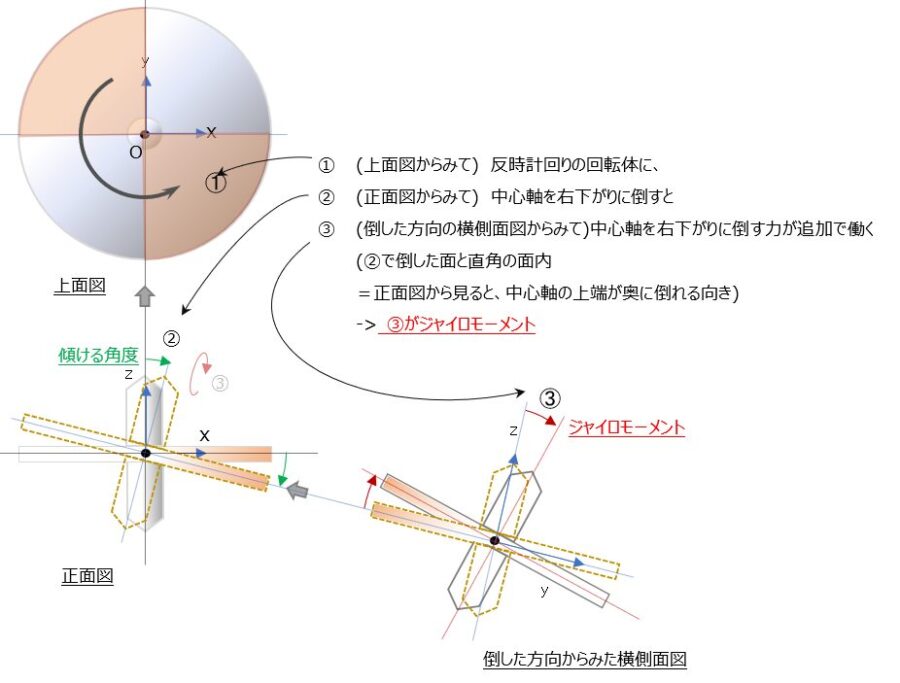
まずは、回転体モデルの設定。以下(円盤+軸からなる剛体の回転体:図 ①)
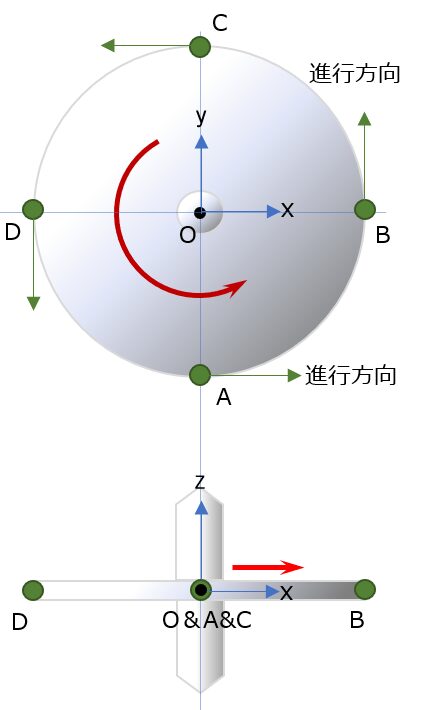
円盤面の中心に原点O、回転の中心軸をZ軸とし(右手系座標)、回転体はZ軸正方向に右ねじ方向で回転しているとする。
x軸とy軸は円盤の面上にとり、
- x軸上にA点&C点
- y軸上にB点&D点
をとる(xy平面:水平面)。以下、この回転体を使って考える。
回転体を傾けた時の(円盤上の)質点の移動方向変化について
この回転体の中心軸(z軸)を、 y軸正方向にて時計周りに傾ける(図②でいうと右下がり方向)。当然、x軸は水平面からx‘軸方向へと向きが変わる。
この時、点B&点Dはそれぞれ
- B点->B’点 (右下がり)
- D点->D’点 (左上がり)
に移動し、またこの傾斜により、A点、C点を通過する質点は水平面から外れB’点方向、D’点方向へと進行方向が変わる
(点B&Dを通過する質点の進行方向は変わらない)。
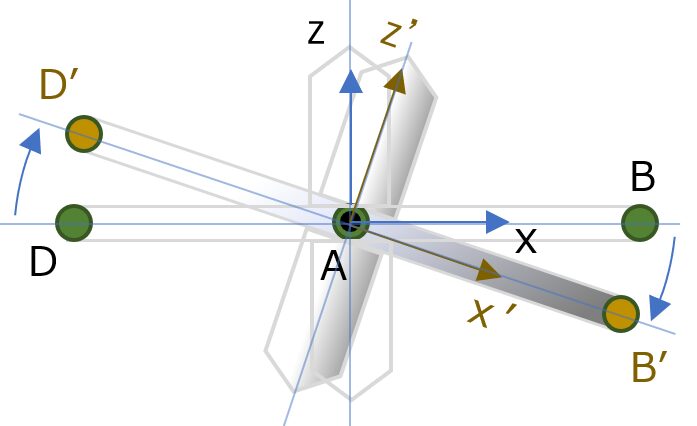
回転体上の質点は、回転軸の傾斜がなければ向心力による水平面内での円運動だけであるが(質点の移動方向の変化は2次元内)、回転軸とは別軸まわりの回転が加わる事により、一部の質点にもう一方向の変化が加わる(最大方向変化:A点&C点)。
点Aを通過する質点に着目する。
点Aを通過する質点からすれば、移動方向が2次元内(水平面内)であった状態から、回転軸とは別軸まわりの回転により新たな方向(B’点方向)へと押し下げられる。つまり、この質点の移動方向変化は、2次元内のみだったものが3次元へと変わる。
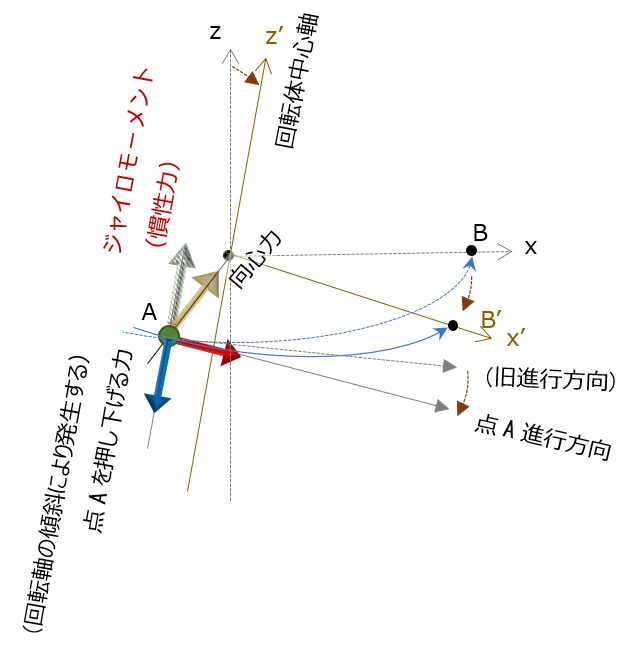
ジャイロモーメント効果を生む慣性力
回転体の中心軸を傾斜させれば、円盤状の質点はその進行方向において回転方向のみならず、垂直方向にも変化する。
つまり質点からすれば、回転方向のみならず追加で”進行方向を変える力”が加えられる事になる。
(例えば、A点には”押し下げる向きの力”が追加で働く)
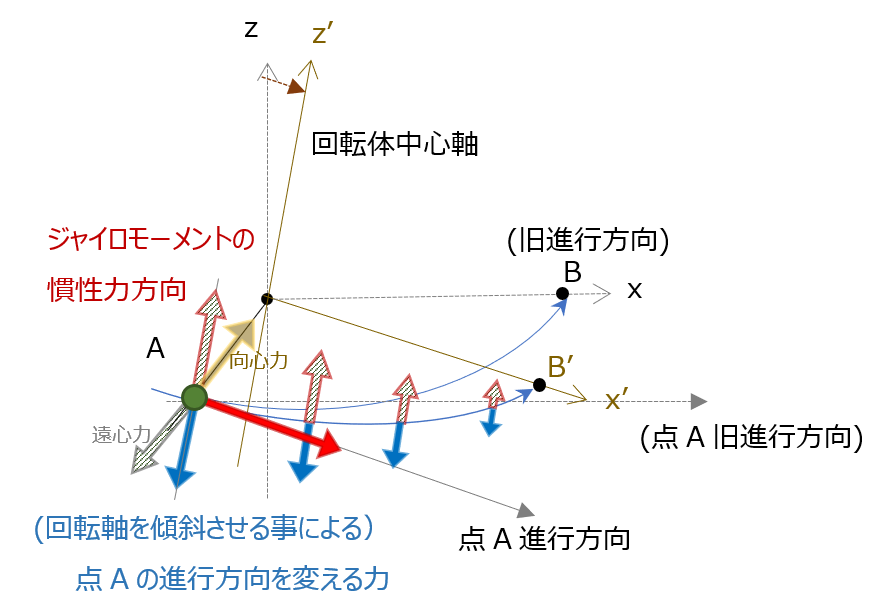
となると、先にも書いたように、この力にも当然ニュートンの運動の第一法則(元の進行方向を維持しようとする性質(慣性))がはたらくため、向きを変えられた質点は動きを維持しようとする。結果、この”向きを変える力”にあがなう動きをしているようにみえる。
これが、例えば円盤上のA点からみれば、質点を”押し上げる向きの力”(上向きの慣性力)として見える慣性力である。
-> この慣性力がジャイロモーメントのもと
つまり、回転軸中心の円上で質点の向きを変えている力(向心力)にあがなう方向の(質点に発生しているように見える)慣性力が”遠心力”であるが、これと同じように回転軸を傾斜させた事により質点の進行方向が傾斜角分だけ変わったことに対して、それにあがなう方向に発生する慣性力から発生するのがジャイロモーメント。
Note:
再度、この力は慣性力(見せかけの力)。質点は元の進行方向を維持させようとしているだけ。
C点についても考え方は同じ。A点とは逆の向きなので、C点には逆の”押し下げる力”が働いているように見える
また、B点とD点を通過する回転体部分の質点については、回転軸を傾けても平行移動するだけなので質点の向きは変わらず。
つまりこの方向には慣性力は発生しない。
まとめれば、手前側(A点側)と奥(C点側)の組み合わせにより、回転体の中心軸を右下がりに傾けると、回転軸の”上端は奥”&”下端”は手前に倒れる追加の動きが発生。
つまり、発生する慣性力は、A点&C点において最大値をとり、B点&D点においては”0”。
以上が、ジャイロ効果( ジャイロモーメント )とその仕組み
(当然、ジャイロ効果は、中心軸を傾斜させている最中にのみ発生)。
ジャイロモーメントが発生する方向
ジャイロモーメントが発生する方向についても覚書
質点の動きを3軸にわければ、
- もともとの進行方向(円の接線方向)、を基準に、
- 遠心力の発生する方向(回転面上に発生し1.に直交)、と
- ジャイロモーメントが発生する方向(1.&2.の双方に直交)
である。当然、それぞれの方向は各々直行している。
以下に3軸の各方向について図示
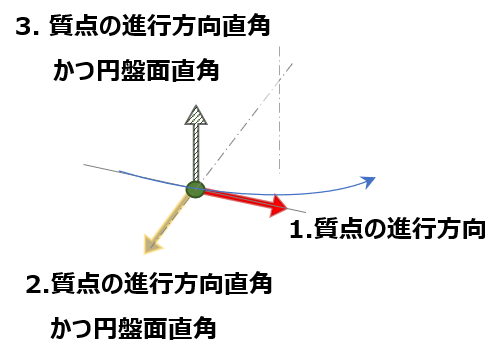
- ひとつは元の進行方向(上図:進行方向)
-> その質点の持っている慣性の進行方向(円の接線方向)
これに直交する残りの2方向のうち、
- ひとつは回転により発生する遠心力方向(上図:遠心力方向)
(=コマの円盤面上かつ質点の進行方向に対して直角方向)
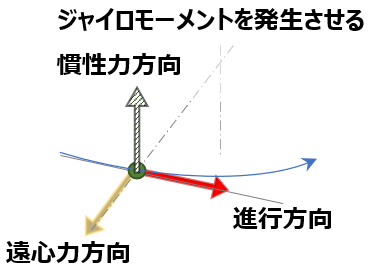
- 最後のひとつがジャイロモーメントが発生する方向(上図:ジャイロモーメントを発生させる慣性力方向)
(=コマの円盤面に直角方向かつ質点の進行方向にも直角)
->つまり、質点の進行方向と遠心力の方向にも直行する方向
冒頭にて”ジャイロモーメントは3次元でとらえる必要がある”と書いたのは、このジャイロモーメントを発生させる慣性力が円盤面から外れ、入力している力以外の方向の3次元方向に働くため
<- 3軸でとらえる必要がある
ジャイロモーメントの向きについての補足
実際このジャイロモーメントが動く方向はいちいち覚えなくとも、、円盤状の一点、点Aに着目して
- 円盤上の点の元の向き(旧進行方向)
- 動かされた向き(現進行方向)
の二つから、軸を傾けたときの点Aの慣性が元はどこに向かっていたのかを考えれば、ジャイロ効果の向きは判断できる。
(上の例では、点Aは水平方向に動いていたのに、それを下げる方向に向けている。慣性力はそれにあがなう方向。つまり上を向く。結果、外からみればコマの中心軸の上端は奥、下端は手前に倒れる。)
動きが3次元になっただけで、慣性力の追っかけ方は遠心力と同じである。
補足:ジャイロ効果の体感
手のひらサイズでジャイロモーメントの大きさを体感できる道具
ちいさなローラーを廻してジャイロモーメントを発生させて手首を鍛える道具だが、こんな小さなローラーがこんな大きなモーメントを発生できるのかとびっくりする。
-> ホントはトレーニング機器。
回転数上がってくるとキーンって音が鳴りだして、限界を試したくなる。。手首がもげそうにけど。。。
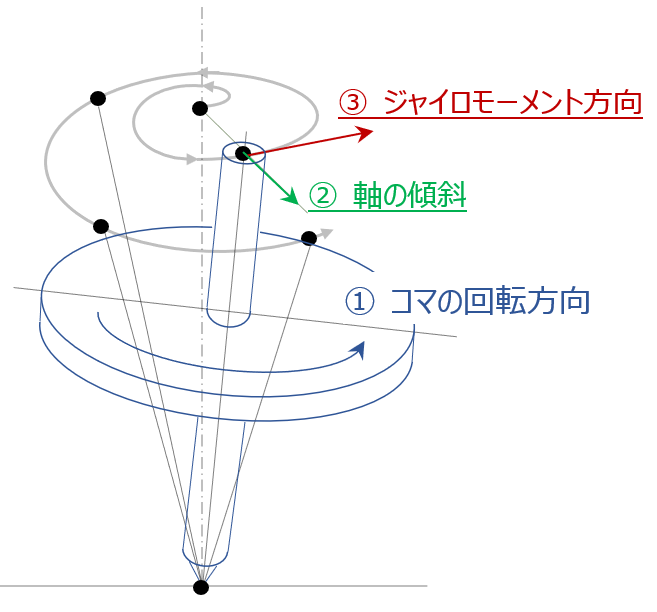
向きについて簡単に観察できるのは、地面の上で回転させるコマが倒れる直前。
地面の上で回っているコマは、回転が落ちるにしたがって中心軸が徐々に傾き転倒に至るのはご存じの通り。この時、軸の頂点が螺旋を描きながら転倒していく事も簡単に観察できる。
この螺旋の向きを決めているのが、前述のジャイロモーメントと重力による軸を傾斜させるモーメント。
中心軸の頂点の螺旋の軌跡は、これが重なった結果の動き。 -> コマの回転方向が、頂点の描く螺旋の向きを決めている
まとめ
結局のところ、ジャイロ効果による動きは、質点が維持しようとしている慣性(速度&方向)がどうなっているか見極めればわかる。
つまり回転体上の質点の慣性の維持から、どの方向に慣性力を発生させているか。。を考えることが、中心軸が追加でどちらに傾くか(ジャイロ効果の発生)、がわかる。
遠心力もジャイロ効果も、この考えで動きを捉えればよい。
追記
機械設計においては、(モータ、エンジン、タイヤ等々)回転体をもつ部品の搭載を検討しなければならない状況は多々ある。特に、移動を前提とする製品に搭載する場合、その回転体の中心軸が傾けられる状況は想定内の状況。
この時にジャイロモーメントも含めた慣性力が、一通りパッと頭に浮かべる事ができる事は、事象の想定/理解/解析に役に立つ事が多い(特に問題が起きた場合)。
まぁ体感してみるのが一番かもしれないが、物理式なくてもその発生の仕組みの感覚はつかめるので、まずは頭の片隅の知識として。。。

