角度の単位
日常生活では、度数での角度表示が一般的(90°とか360°とか)。
これに対し、数学、物理では角度の単位はπを使ったラジアン(radian)の表示が主に使用される
圧倒的に使い勝手が良いからである。(昔はどっちでもいいじゃん。。と思ってたけど。。)
度数表示の360° を ラジアン表示の2πにするのも理由がある。
ラジアン表記を使う理由
まずは、360°がラジアン表示で2π(rad)になる理由から。
ざっくりといえば、半径=1の円の全周長が2πであるから。この ”長さ2πの周長” を全周角の表示に使っているだけである。
(任意の角度は全周角に対する割合で表示されるので、実は、基準となる全周角は360°表示であろうが2πと表示しようが、表示だけであればどちらでもたいして困らない。)
ただ、2πを基準にするメリットが確かにある。(特に物理とかで)例えば円運動を取り扱う時に、円周の”長さ”に関連づけてみる事が容易になり、お、そっか、当たり前か!と思う事が増える。
この辺を以下に。。
ラジアン表記の見方と意味
さて、一般的な 半径rの円の全周Lは ”直径 x 円周率π”、
\(L=(2r) \cdot \pi \)
これを、ラジアンの ”全周角2π (rad)”が使われているとみれば
\(L=r\cdot (2\pi) \) ・・・⓪
つまり、半径rの円の周長Lは ”半径rx ”全周角2π (rad)”。
ここで、2πを長さとしてみれば、Lは、”半径1の円の全周長(2π)”の”r倍” とも見る事もできる。
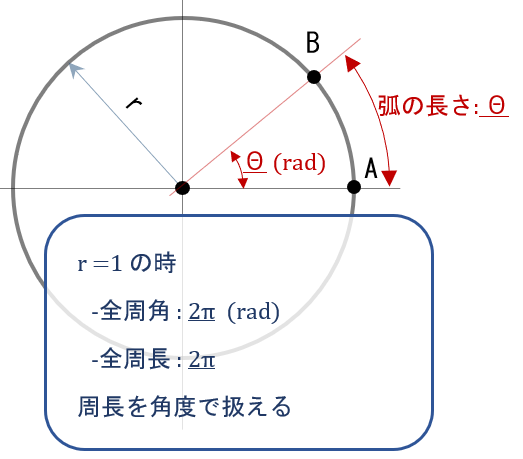
さて、ラジアン表示の任意の角度θ(rad)は、全周角2πに対する割合から表示される。
つまり半径1の円であれば、その角度で切り取った”円弧の長さ”を直接あらわす。
(例えば、角度90°はラジアン表示でπ/2(rad)、半径1(m)の円を角度90度で切り取った時の円弧の(短い方の)長さもπ/2(m))
という事は、⓪式のL=r・2π・・・⓪ を利用して、この全周角”2π” 部分を任意の角度 θ(rad)で置き換えれば、半径rの円をθで切り取った円弧の実の長さ Lp が直接求まる。
Lp=r・θ (詳細次章)
要は、Lpは半径r=1の円をθで切り取った弧の長さをr倍したものという見方。
(これが、”長さ基準でも見る”、の入り口。ちょっとわかりにくいかもしれないので、後述で別の例を。。)
ラジアン表示に一回もどって。。。以下に。。
単位 ラジアン(rad)
再度、円の全周長 La は、半径をrとすれば
\(L_a=\sf{r}\cdot (2\pi) \)
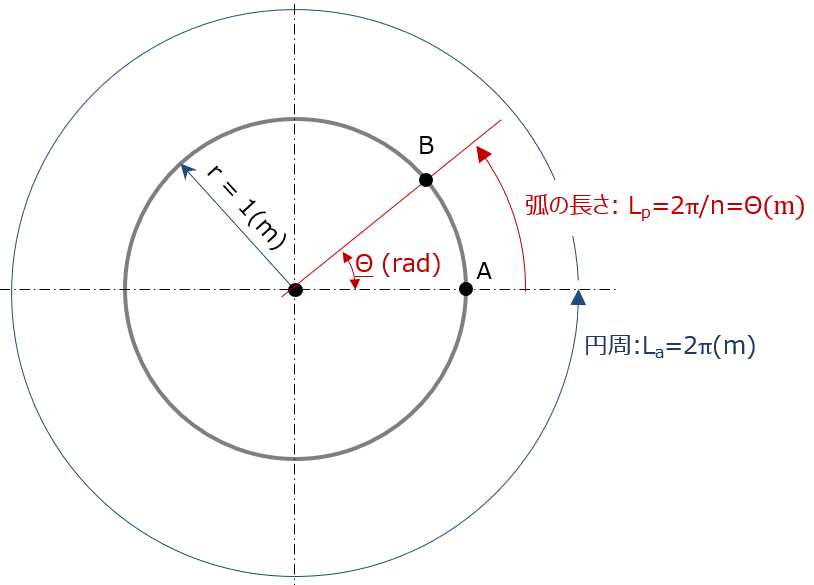
中心を含むように円を1/n((n>0))切り取ると、その切り取った円弧の長さLp (m) は、
\( \begin{align} L_p
&=(\frac{1}{n})\cdot L_a \\[6pt]
&=(\frac{1}{n})\cdot 2\sf{r}\pi \\[6pt]
&=r\cdot (\frac{2\pi}{n}) ・・・①
\end{align} \)
ここで、θ (rad) = 2π/n とすれば
\( L_p =\sf{ r} \cdot θ \) ・・・②
まとめれば、
例:ラジアン(radian)表記が便利な場面
さて、利用例。回転運動を表すときに使う”角速度”も、直線運動の”速度”の定義と同じ見方で理解できる。
回転運動の場合、実移動距離は直線ではなく弧の長さとなるが、ここに前述の ②式( Lp=rθ )を使えばよい。
例えば、平均速度の定義は直線運動の場合、
平均速度=(実移動距離)/(時間) ・・・③
であるが、回転運動中の物体の平均速度vrにも同じ見方をして
vr=Lp / t (m/s) ・・・④
とすれば、これに②式を代入して
\( \begin{align} v_r
&=\frac{L_p}{t}\\[6pt]
&=\frac{r\cdot θ}{t}\\[6pt]
&=r\cdot \frac{θ}{t} ・・・⑤
\end{align} \)
また、ここの ”θ/ t” は、単位時間あたりの角度となるので、これを角速度ωとして
ω=θ/ t (rad/s) ・・・⑥
と定義する。 ⑤式を書き直せば、
vr=rω ・・・⑦
と、シンプルに回転運動の速度が表す事ができる。また、この見方で(⑦式も公式としてではなく)円運動の速度もただ実距離を時間でわっているだけね、で理解できる。便利便利。。
