ベクトルとは
ベクトルとは空間上の始点（A）と終点（B）の二点を結ぶ線分。 この始終点を持つことにより、
- 大きさ（長さ）
- 向き（始点->終点）
の”二つの量を同時に持つ”。
基本はこれだけだが、上記の複数情報を一つの形で持つことができ、またそのままの形で計算可となるため、数学、物理にて多用される（ベクトル計算後に成分値算出等々）。
ベクトルの定義と書き方
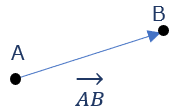
二点AとBを使い点Aから点Bに向かうベクトルは \( \overrightarrow{AB} \) として表す。
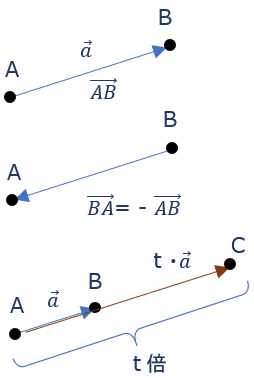
また、”点Aから点Bへ向かうベクトルを\( \vec{a} \) とする” の様に定義すれば、簡易表示するのも可 → ベクトル計算の式が見やすくなる
また、ベクトルの向きは変えず、大きさをt倍したものを\( t \cdot \vec{a} \ (= t \cdot \overrightarrow{AB}) \) と書く。
始点と終点を入れ替えたベクトル \( \overrightarrow{BA} \) は、\( \overrightarrow{AB} \) とは向きが反対。マイナスを使って、\( \overrightarrow{BA} \) = \( – \overrightarrow{AB} \) にて表す。
ちなみに、ベクトルに対し大きさを表す量はスカラー量と呼ばれる（上でいえばｔ）。
- t : スカラー量 （ ちなみに、 \( t \cdot \overrightarrow{AB} \) はベクトル量）
また、”大きさ（長さ）” と ”向き” が同じであれば、同一ベクトル。
つまり平行移動させても、ベクトルとしては同じ。
ベクトル座標と成分計算
まず、任意の点Ｏを中継させる場合を考える。
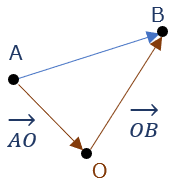
図③をみれば、\( \overrightarrow{AB} \) = \( \overrightarrow{AO} + \overrightarrow{OB} \) であること、
また \( \overrightarrow{AO} \) = \( – \overrightarrow{OA} \) である事を使えば
\( \overrightarrow{AB} \) = \( \overrightarrow{OB} – \overrightarrow{OA} \) ・・・①
(ちなみに、中継点基準に終点側から始点側のベクトルをひくだけ：図③参照)
これを使って、成分計算をする。
Oを原点にもつO-XYZ座標系（直行座標）があるとする。
O-XYZ上の 点A & 点B の座標が
- 点A: \( ( x_a~,~y_a~,~z_a ) \)
- 点B: \( ( x_b~,~y_b~,~z_b ) \)
とすれば、
①式より、\( \overrightarrow{AB} \) の成分\( \left ( \begin{array}{c} \alpha_x \\ \alpha_y \\ \alpha_z \end{array} \right ) \) は \( \overrightarrow{AB} \) = \( \overrightarrow{OB} – \overrightarrow{OA} \) より、成分表示すれば
\( \left ( \begin{array}{c} \alpha_x \\ \alpha_y \\ \alpha_z \end{array} \right ) =\left ( \begin{array}{c} x_b \\ y_b \\ x_b \end{array} \right ) – \left ( \begin{array}{c} x_a \\ y_a \\ x_a \end{array} \right ) = \left ( \begin{array}{c} x_b-x_a \\ y_b -y_a\\ z_b-z_a \end{array} \right ) ・・・① \)
となる。
ベクトルの大きさ
ベクトルの大きさは、\( | \overrightarrow{AB} | \) で表記される。
その値は①を使って
\( \begin{align} | \overrightarrow{AB}| &= \sqrt{ {\alpha_x}^2 + {\alpha_y}^2 +{\alpha_z}^2} \\[4pt] &= \sqrt{ (x_b-x_a)^2 + (y_b-y_a)^2 +(z_b-z_a)^2} \end{align} \)
-> 見ての通り、２点間の距離を求める式と同じ。
追記
さて、以上を踏まえて、内積、外積の計算へ。内積＆外積の意味がわかるとベクトルの世界がぐっと広がる
