はじめに
ベクトルの定義については前回の記事を参照
引き続きベクトル内積&外積へ。内積も外積も使い道が明確にある便利な道具。道具も使い方を知っていると、より使いやすくなる。
まずは内積から。その定義と計算方法/計算則。
ベクトルの内積 (dot-product)
内積の定義
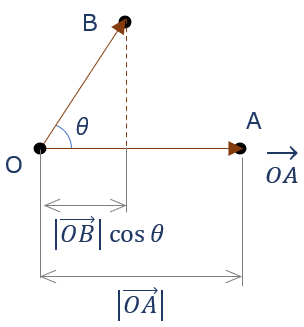
\( \small \overrightarrow{OA} \)、\( \small \overrightarrow{OB} \) のなす角 \( \theta \) とする。この時 \( \small \overrightarrow{OA} \)、\( \small \overrightarrow{OB} \) の内積は
\( \small {\overrightarrow{OA} \cdot \overrightarrow{OB} = |\overrightarrow{OA}|\cdot |\overrightarrow{OB}| \cos \theta } \) ・・・①
で定義される。つまり内積はスカラー量であり、これは\( \small{ (|\overrightarrow{OA}|} ) \cdot ( \small {|\overrightarrow{OB}|} \cos \theta ) \) とみれば、
\( ( \small{\overrightarrow{OA}} \) の長さ) x \( ( \small{\overrightarrow{OB}} \) の \( \small{\overrightarrow{OA}} \) への投影長)
の掛け算を意味する。
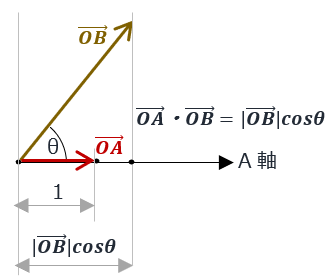
また、この”投影”を利用すれば、 \( \small {|\overrightarrow{OA}|} \) =1の時には、” \( \small {\overrightarrow{OB} } \) の \( \small {\overrightarrow{OA}} \) 方向への投影長” を意味し、これは座標値算出そのまま。
追記:座標値算出
再度、\(\small {|\overrightarrow{OA}|} \) =1の時の内積値 \( \small { \overrightarrow{OA} \cdot \overrightarrow{OB} }= \small {|\overrightarrow{OB}| } \cos \theta\) は、
- \( \small {\overrightarrow{OB}} \) のA軸方向に投影したときの長さ
-> ”A軸上の座標成分”
この見方はよく使う
ちなみに、座標軸変換に使っている例はこちら。オイラー角(回転行列)へつながっていくのだが、紐解けばこまごまとベクトルの内積計算を積み上げているだけ。
内積の計算則
内積の分配法則 (後述の成分計算(④式)から成立している事は容易に確認できる)
\( \vec{a} \cdot ( \vec{b}+\vec{c} )= \vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c} \)・・・②
\( ( \vec{b}+\vec{c}) \cdot \vec{a} = \vec{b} \cdot \vec{a}+\vec{c} \cdot \vec{a} \)・・・③
内積の成分計算
\( \small {\overrightarrow{OA}} \) の成分を \( (x_a, y_a, z_a) \)、\( \small {\overrightarrow{OB}} \) の成分を \( (x_b, y_b, z_b) \) とすれば
\( \small {\overrightarrow{OA} \cdot \overrightarrow{OB} } \) = \( x_a \cdot x_b + y_a \cdot y_b+ z_a \cdot z_b \) ・・・④
である。これは導いておく。
まず、Oを原点にもつ \( \small {O-XYZ} \) 座標系(直行座標)を設定する。
\( \small {O-XYZ} \) 座標の \( x \) 軸、\( y \) 軸、\( z \) 軸の単位ベクトルを \( \vec{i} \) = \( \left ( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right ) \) 、\( \vec{j}\) = \(\left ( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right )\)、\( \vec{k}\) = \(\left ( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right )\) とすれば、これらの各単位ベクトルは互いに直行。
よって、内積の定義からこれらは以下の性質を持つ。
\( \vec{i} \)・\( \vec{j} \) = \( \vec{j} \)・\( \vec{k}\) = \( \vec{k} \)・\( \vec{i} \) = 0・・・⑤
\( \vec{i} \)・\( \vec{i} \) = \( \vec{j} \)・\( \vec{j} \) = \( \vec{k} \)・\( \vec{k} \) = 1・・・⑥
(全て単位ベクトル、かつ、ベクトルの間の角が直行 ( \( cos\dfrac{\pi}{2}=0 \)) していれば内積は ”0”、同一方向 ( \( cos0=1 \)) であれば”1”)
さて、\( \small {O-XYZ} \) 上の点A、B座標をそれぞれ
点A : \( ( x_a \ , \ y_a \ , \ z_a ) \)
点B : \( ( x_b \ , \ y_b \ , \ z_b ) \)
とすれば、\( \small {\overrightarrow{OA}} \)、\( \small {\overrightarrow{OB}} \) は各軸の方向ベクトルでもある\( \vec{i} \)、\( \vec{j} \) 、\( \vec{k} \)を使って
\( \small {\overrightarrow{OA}} \) = \( x_a \cdot \vec{i} +y_a \cdot \vec{j} +z_a \cdot \vec{k} \)
\( \small {\overrightarrow{OB}} \) = \( x_b \cdot \vec{i} +y_b \cdot \vec{j} +z_b \cdot \vec{k} \)
と書ける。これに②③式、および⑤⑥式の特徴を使えば、\( \small {\overrightarrow{OA}} \)、\( \small {\overrightarrow{OB}} \)の内積値は、
\( \begin{align}
\overrightarrow{OA} \cdot \overrightarrow{OB}
&= ( x_a \cdot \vec{i} +y_a \cdot \vec{j} +z_a \cdot \vec{k}) \cdot (x_b \cdot \vec{i} +y_b \cdot \vec{j} +z_b \cdot \vec{k}) \\[8pt]
&= (x_a \cdot x_b ) \vec{i} \cdot \vec{i}+ ( y_a \cdot y_b ) \vec{j} \cdot \vec{j}+ ( z_a \cdot z_b ) \vec{k} \cdot \vec{k} \\[8pt]
&= x_a \cdot x_b + y_a \cdot y_b+ z_a \cdot z_b ・・・④
\end{align} \)
と成分値同士の計算結果によっても求まる。
→ 各々のベクトルの成分同士(x成分、y成分、z成分同士)を掛け合わせた値の総和が内積値。
ベクトルをn次元に拡張しても、この内積計算は同じ。
(n次元のベクトルの各軸の成分同士を掛け合わせた値の総和が内積値)
追記
続いてベクトルの外積。次の記事にて。