はじめに
あまり意識せずに読み飛ばしてしまうことが多いが、ベクトル/行列の計算を見ると、”正規直行性”、”正規直行基底” の単語がよく出てくる。
読み飛ばす事もあるが少しこだわると、なんだそういう事ね。。がふえるから不思議（座標軸変換とかはこれが前提条件）。
例えば、正規直行基底（とベクトルの内積）を組み合わせれば、以下の回転行列の仕組みもずっとわかりやすくなるはず。
まずはベクトルの正規性から。
正規性（nomality）とは
ベクトルが正規性を持つとは、そのベクトルの長さ (大きさ) が ”１” である事を指す。
また逆にベクトルを正規化するとは、そのベクトルの長さを ”１”にする事。
つまり
である。
また、正規化されて長さが”1”となったベクトルは単位ベクトルと呼ばれる。式で書けば \( |\vec{u}| \) ＝１。
直行性 （orthogonality）とは
ベクトルが直行性をもつとは、その字の通り互いのベクトルが直行している事
”ベクトルの直行化” (直行ベクトルを求める事) についてはここでは割愛。
正規直行性 / 正規直行基底とは
ｎ次元空間は、基底となるｎ個のベクトルにより定める事ができる。（独立した（＝向きの異なる）ｎ個のベクトル）
つまり、空間の次元を決めるモトになるベクトルのセット。
正規直行性と座標
では、正規性と直行性の二つをあわせた正規直行性が、いったい何の役に立つかについて。要は、互いに直行する長さ１のベクトルセットの使い道（正規性＆直行性）。
結論から言えば、長さが１のベクトルが互いに直行している事から、その次元に方眼紙のような目盛づけの働き。つまり、座標軸。 <- 空間上の位置表示に使える。
空間上にて正規直行性を確保した軸にて座標系を設定すれば、（ベクトルの内積を使い）その設定した座標系上の任意の点の座標値が算出できるようになる。
以下にその話を
正規性の使い方 （ベクトルを使った座標値表示）
まずは入り口として正規性の使い方から。一次元を例にとり説明（数直線をイメージ：ベクトル方向は1方向のみ）。
任意のベクトルを \( \vec{a} \) とし、単位ベクトルを \( \vec{u} \) とする
この時、\( \vec{a} \) は \( \vec{u} \) のスカラー倍 s で表現できる。
\( \vec{a} \) = \( s \cdot \vec{u} \) ・・・①
この時 \( \vec{u} \) 方向に座標軸を設定し原点Oに \( \vec{a} \) の始点をとれば、①の スカラー量 s はその座標軸上の \( \vec{a} \) の座標値になる（ ∵ \( \vec{u} \) =1 ）。
さて、これに直行性を加えて二次元に。。
正規直行性の使い方 （座標系におけるベクトル利用）
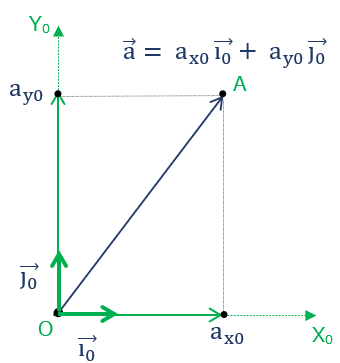
何もない平面（二次元）に座標軸を設定する。まず平面上の一点 \( O \) をとり、それを原点に直行する二つの軸を引く。二つの軸を \( \small{X_0} \) 軸、\( \small{Y_0 }\) 軸 とする。
この二つを \( \small{O-X_0Y_0} \) 座標系の軸とすれば、まずは何もなかった平面上に基準点 \( O \) と方眼紙の向きがきまる。
次に方眼紙の目盛りづけ（座標値）。
互いに直行する二つの正規直行基底ベクトル \( \overrightarrow{i_0} \) 、\( \overrightarrow{j_0} \) を使い、\( \overrightarrow{i_0} \) を \( \small{X_0} \) 軸方向、\( \overrightarrow{j_0} \) を \( \small{Y_0} \) 軸方向に一致させれば、 \( \overrightarrow{i_0} \) 、\( \overrightarrow{j_0} \) の 成分（座標値）は、直行している事、大きさは１である事からそれぞれ、
\( \vec{i_0}= \left ( \begin{array}{c}
x_{0}\\
y_{0} \\
\end{array} \right )
= \left ( \begin{array}{c}
1\\
0\\
\end{array} \right ) \) , \( \vec{j_0}= \left ( \begin{array}{c}
x_{0}\\
y_{0} \\
\end{array} \right )
= \left ( \begin{array}{c}
0\\
1\\
\end{array} \right ) \) ・・・②
とかける。
さて、 \( \small{O-X_0Y_0} \) 上に任意の点Aをとり, 原点を始点とするベクトルを\( \overrightarrow{OA} (\ = \ \vec{a}) \) を考える。
\( \overrightarrow{i_0} \) と \( \overrightarrow{j_0} \) のベクトルの足し算で表せば、\( \vec{a} \) は、
\( \vec{a}=a_{x0}\cdot \vec{i}_0+a_{y0}\cdot \vec{j}_0 \)・・・③
（ax0 、ay0：スカラー量）
よって、
\( \vec{a}= a_{x0}\left ( \begin{array}{c}
1\\
0\\
\end{array} \right ) +
a_{y0}\left ( \begin{array}{c}
0\\
1\\
\end{array} \right ) = \left ( \begin{array}{c}
a_{x0}\\
a_{y0}\\
\end{array} \right ) \) ・・・④
\( \small{O-X_0Y_0} \) 座標軸は、正規直行ベクトルの \( \overrightarrow{i_0} \) と \( \overrightarrow{j_0} \) と一致しているため、 点Ａの座標は③式のベクトルの成分値がそのまま座標値となる。つまり、
\( \left ( \begin{array}{c}
x_{0}\\
y_{0} \\
\end{array} \right )
= \left ( \begin{array}{c}
a_{x0}\\
a_{y0}\\
\end{array} \right ) \) ・・・⑤
要は、座標軸方向を示すベクトルが互いに直角（正規直行基底）であれば、ベクトルの足し算に使われる係数 \( a_{x0} \) と \( a_{y0} \) が、点Aの座標値 \( (a_{x0}, a_{y0}) \) と一致する。
（座標軸が”直行”していることから、 \( \vec{a} \) のそれぞれの軸への投影長が各軸の座標値となるのは当たり前ではあるが、とりあえずこれを頭の片隅に。。）
念のため、座標軸が”直行していない”場合の座標値とベクトル成分値について。
つまり、直行していない座標系 \( \small{O-X_aY_a} \) の基底ベクトル \( \overrightarrow{i_a} \)、 \( \overrightarrow{j_a} \) としてみると
この \( \small{O-X_aY_a} \) での
- 点Ａの座標：\( (a_{xa}, a_{ya}) \)
- ベクトルの足し算： \( \vec{a}=a_{x0} \cdot \vec{i}_a + a_{y0} \cdot \vec{j}_a \) の係数 \( a_{x0} \) 、 \( a_{y0} \)
は、当然一致しない（右図）。
つまり、\( \vec{a} \) の座標軸への投影長（ベクトルの成分値）は、\( \small{O-X_aY_a} \) の座標値算出には使えない。
（＝直行していない座標軸ではベクトルが座標値算出に使えない、というか使うにしても不便）
投影長がらみのベクトルの内積については、こちらを
正規直行性と内積を使った座標値算出
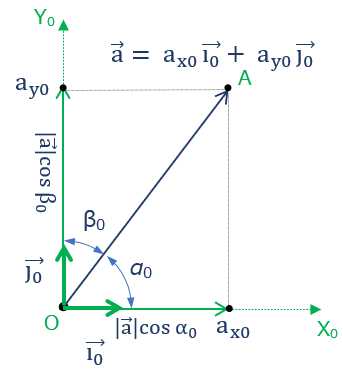
さて、ベクトルの内積を使った座標値の算出過程にベクトルの内積をからめてもう少し。
正規直行している二つのベクトル\( \overrightarrow{i_0} \)、 \( \overrightarrow{j_0} \) ( |\( \overrightarrow{i_0} \)| = | \( \overrightarrow{j_0} \) | = 1 ）と \( \vec{a} \) との内積を求めれば
\( \begin{align}
\overrightarrow{a} \cdot \overrightarrow{i_0} &= |\overrightarrow{a}| \cdot |\overrightarrow{i_0}| \cdot cos{α_0}\\[6pt]
&= |\overrightarrow{a}| \cdot cos{α_0} \\[6pt]
& =a_{x0}
\end{align} \)
であり、
\( \begin{align}
\overrightarrow{a} \cdot \overrightarrow{j_0} &= |\overrightarrow{a}|\cdot|\overrightarrow{j_0}|\cdot cos{β_0}\\[6pt]
&= |\overrightarrow{a}|\cdot cos{β_0}\\[6pt]
&= a_{y0}
\end{align} \)
( \( α_0 \) : \(\overrightarrow{a} \) と \(\overrightarrow{i_0} \) のなす角、\( β_0 \) : \(\overrightarrow{a} \) と \(\overrightarrow{j_0} \) のなす角 )
つまり
よって、内積をつかって座標値を表現すれば、
\( \left ( \begin{array}{c}
x_{0}\\
y_{0} \\
\end{array} \right )
= \left ( \begin{array}{c}
a_{x0}\\
a_{y0}\\
\end{array} \right )
= \left ( \begin{array}{c}
\vec{a}\cdot \vec{i}_0\\
\vec{a}\cdot \vec{j}_0\\
\end{array} \right ) \) ・・・⑥
で表せる。
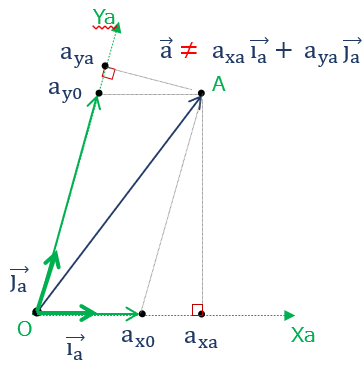
点を変えずに座標軸を動かす（座標軸変換）
さて、⑥式では正規直行ベクトルの \(\overrightarrow{i_0} \) と \(\overrightarrow{j_0} \) に \( \small{X_0} \) , \( \small{Y_0} \) 軸方向を一致させた内積計算（投影）から
\( \vec{i}_0= \left ( \begin{array}{c}
x_{0}\\
y_{0} \\
\end{array} \right )
= \left ( \begin{array}{c}
1\\
0\\
\end{array} \right ) \) , \( \vec{j}_0= \left ( \begin{array}{c}
x_{0}\\
y_{0} \\
\end{array} \right )
= \left ( \begin{array}{c}
0\\
1\\
\end{array} \right ) \)
となっている。
さて、この内積は、”任意のベクトル\( \vec{a} \) を単位ベクトル側 (\( \overrightarrow{i_0} \) と \( \overrightarrow{j_0} \) ) への投影長を算出しているだけ”、である事を踏まえれば、\( \small{X_0} \) , \( \small{Y_0} \) 軸 ”以外” の 任意の軸にも使う事ができる。
例えば、、
\( \small{O-X_0Y_0} \) 座標系上に各軸方向と向きの異なる \( \overrightarrow{i_1} \) と \( \overrightarrow{j_1} \) （二つは正規直行）があり、これを使って新しい座標系 \( \small{O-X_1Y_1} \) を設定したとする。
この時、O-X1Y1上の任意ベクトル a の座標値 \( \left ( \begin{array}{c}
x_{1}\\
y_{1} \\
\end{array} \right ) \) は、
\( \left ( \begin{array}{c}
x_{1}\\
y_{1} \\
\end{array} \right )
= \left ( \begin{array}{c}
\vec{a}\cdot \vec{i}_1\\
\vec{a}\cdot \vec{j}_1\\
\end{array} \right ) \) ・・・⑦
である。
つまり、内積計算の各軸の単位ベクトルを入れ替えるだけで 新たな座標系上の\( \small{O-X_1Y_1} \) 上の座標値が算出できる。
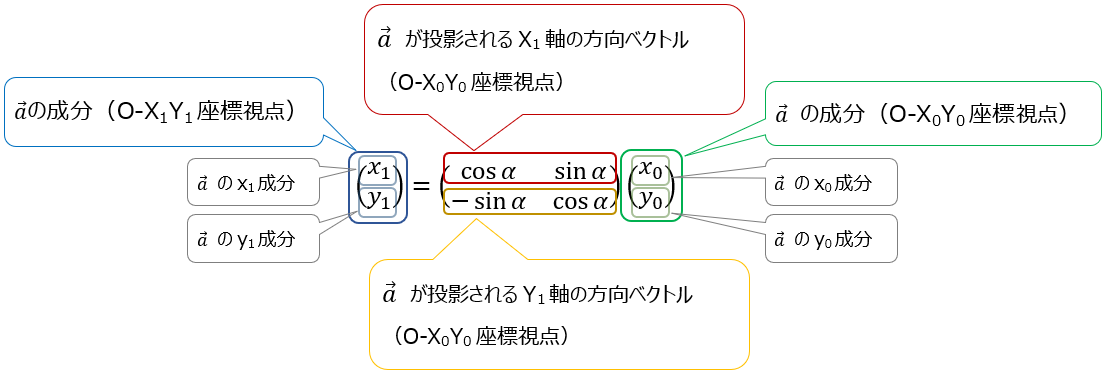
これがわかれば、座標変換（例えば回転行列）の正体が見えてくる。⑦式を行列で組みなして角度情報を加えるみる。つまり
\( \small{O-X_0Y_0} \) と \( \small{O-X_1Y_1} \) のなす角を \(α \) とすれば ( = \( \small{O-X_0Y_0} \) を反時計周りに角度 \(α \) だけ回転させた座標系が \( \small{O-X_1Y_1} \) ) 、
\( \small{O-X_0Y_0} \) から見た \( \small{O-X_1Y_1} \) 座標系の基底ベクトルが、\( \vec{i}_1= \left ( \begin{array}{c}
cos α\\
sin α\\
\end{array} \right ) \) , \( \vec{j}_1= \left ( \begin{array}{c}
-sin α\\
cos α\\
\end{array} \right ) \) であり、
また \( \vec{a}= \left ( \begin{array}{c}
x_{0}\\
y_{0} \\
\end{array} \right ) \) である事から、⑦式の各成分計算を行えば、
\( \left ( \begin{array}{c}
x_{1}\\
y_{1} \\
\end{array} \right )
= \left ( \begin{array}{c}
cos α\cdot x_{0}+sin α\cdot y_{0}\\
-sin α\cdot x_{0}+cos α\cdot y_{0}\\
\end{array} \right ) \)
整理をすれば、
\( \left ( \begin{array}{c}
x_{1}\\
y_{1} \\
\end{array} \right ) = \left ( \begin{array}{cc}
cos α&sin α\\
-sin α&cos α \\
\end{array} \right ) \left ( \begin{array}{c}
x_{0}\\
y_{0} \\
\end{array} \right ) \)
にて、よく見る回転行列（座標変換行列）が表れる。
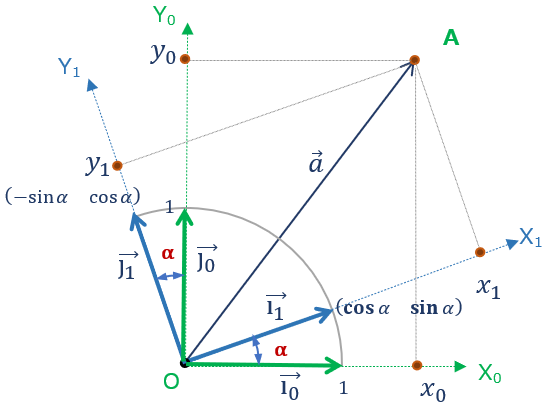
計算過程からわかるが、、、それぞれの意味するトコロはざざっと
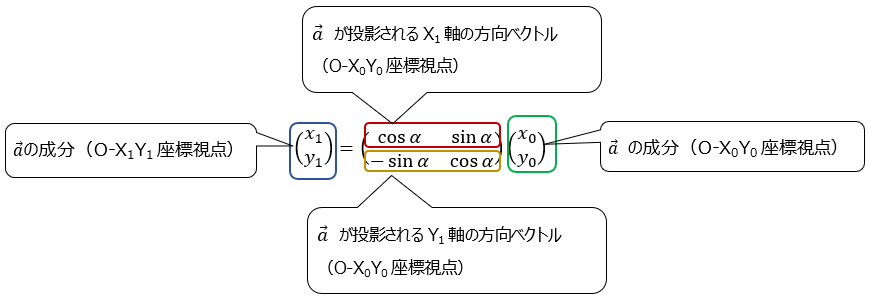
といった感じ。詳細は以下にて
