目次
はじめに
回転行列の見かたについては、前回の記事にて
この記事ではベクトルの内積(投影長)を切り口に行列の積を組み合わせた軸変換とその見かた、そこから回転行列への展開までを書いた。
今回は回転行列の中身を再度。方向余弦を使って導く。
まずは、図的に理解しやすい平面の回転行列(2×2 行列)からはじめて、3次元の回転行列( 3×3 行列 ) へと話をすすめる。
ま、とりあえず3次元の回転行列までおさえておけば、大概なんとかなる
(オイラー角とかとか)。。
二次元(平面)での回転行列
まずは方向余弦を使った座標変換から
(2x2行列):二次元(平面)
使用する座標軸
共通の原点Oをもつ、二つの座標系 O-X0Y0 と O-X1Y1 を考える。
座標軸は右手系、角度はX軸をY軸に向かう方向に回転させる向きを正)とする。ここで
- X0軸方向、Y0軸方向 の 各単位ベクトル
X0軸方向:\(\overrightarrow{i_0} \) 、Y0軸方向:\(\overrightarrow{j_0} \) - X1軸方向、Y1軸方向 の 各単位ベクトル
X1軸方向:\(\overrightarrow{i_1} \) 、Y1軸方向:\(\overrightarrow{j_1} \)
とする。
各軸の方向余弦
O-X0Y0から見たX1Y1 各軸の方向余弦
二つの座標系 O-X0Y0 と O-X1Y1 の各軸についてお互いのなす角を
- X1軸がX0軸、 Y0軸となす角
:\(α_0、β_0 \) - Y1軸がX0軸、 Y0軸となす角
:\(α_1、β_1 \)
とする(X0軸 ,Y0軸は直行より、 \( α_0 +β_0 = \dfrac{\pi}{2} \)、\(α_1 +β_1 = \dfrac{\pi}{2} \) )。
また、このO-X0Y0 の座標軸の方向ベクトル \(\overrightarrow{i_0}=\left ( \begin{array}{c} 1\\ 0 \end{array} \right )\) 、\(\overrightarrow{j_0}=\left ( \begin{array}{c} 0\\ 1 \end{array} \right ) \) を使えば、\(\overrightarrow{i_1} \) 、\(\overrightarrow{j_1} \) はそれぞれ、
\( \begin{align} \overrightarrow{i_1}&= \cos\alpha_0\cdot \overrightarrow{i_0} + \cos\beta_0\cdot \overrightarrow{j_0} =\cos\alpha_0\left ( \begin{array}{c} 1\\ 0 \end{array} \right ) +\cos\beta_0\left ( \begin{array}{c} 0\\ 1 \end{array} \right ) \\ &=\left ( \begin{array}{c} \cos\alpha_0\\ \cos\beta_0 \end{array} \right ) ・・・① \end{align}\)
\( \begin{align} \overrightarrow{j_1}&= \cos\alpha_1\cdot \overrightarrow{i_0} + \cos\beta_1\cdot \overrightarrow{j_0} =\cos\alpha_1\left ( \begin{array}{c} 1\\ 0 \end{array} \right ) +\cos\beta_1\left ( \begin{array}{c} 0\\ 1 \end{array} \right ) \\& =\left ( \begin{array}{c} \cos\alpha_1\\\cos\beta_1 \end{array} \right ) ・・・② \end{align}\)
この余弦(cos)を使った方向ベクトル表示は、方向余弦とよばれる。
よって、
- 座標系 O-X0Y0 からみた ”X1軸方向の方向余弦” は、\( \overrightarrow{i_1}=\left ( \begin{array}{c} \cos\alpha_0\\\cos\beta_0 \end{array} \right ) \)
- 座標系 O-X0Y0 からみた ”Y1軸方向の方向余弦” は、 \(\overrightarrow{j_1}=\left ( \begin{array}{c} \cos\alpha_1\\\cos\beta_1 \end{array} \right ) \)
となる。
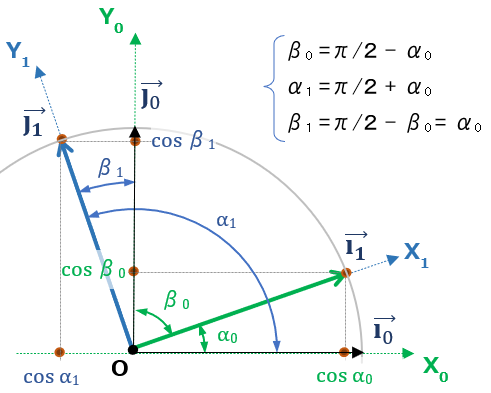
また、\(\overrightarrow{i_1}\)、\(\overrightarrow{j_1}\) は、定義から原点Oが始点の大きさ1のベクトル。角度は任意にとる事ができるので、ベクトルの終点の軌跡は円を描く。
(円の公式に当てはめれば)以下も成立
\( cos^2α_0 + cos^2β_0 = 1\)、\( cos^2α_1 + cos^2β_1 = 1 \)・・・③
O-X1Y1から見たX0Y0 各軸の方向余弦
また逆に X1軸&Y1軸 側から、X0軸&Y0軸のなす角は、
- X0軸がX1軸、 Y1軸となす角
:\(α_0、α_1 \) - Y0軸がX1軸、 Y1軸となす角
:\(β_0、β_1 \)
O-X1Y1座標系 からみた X1 座標軸の方向ベクトル \( \overrightarrow{i_1}=\left ( \begin{array}{c} 1\\ 0 \end{array} \right ) \) と Y1 座標軸の方向ベクトル \( \overrightarrow{j_1}=\left ( \begin{array}{c} 0\\ 1 \end{array} \right ) \) を使えば、O-X1Y1 上の \(\overrightarrow{i_0} \)、\(\overrightarrow{j_0} \) は①②式同様に
\(\overrightarrow{i_0}= \cosα_0\cdot \overrightarrow{i_1} + \cosα_1\cdot \overrightarrow{j_1} =\left ( \begin{array}{c} \cosα_0 \\ \cosα_1 \end{array} \right ) ・・・④ \)
\(\overrightarrow{j_0}= \cosβ_0 \cdot \overrightarrow{i_1} + \cosβ_1\cdot \overrightarrow{j_1} =\left ( \begin{array}{c} \cosβ_0 \\\cosβ_1 \end{array} \right ) ・・・⑤ \)
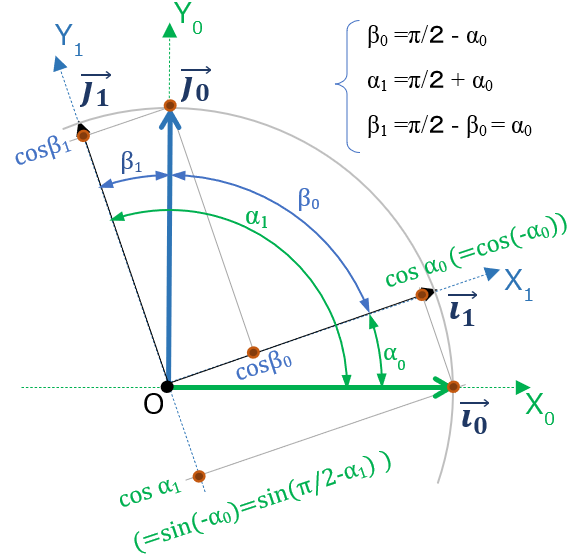
つまりO-X1Y1 上からみて
- 座標系 O-X1Y1 からみた ”X0軸方向の方向余弦” は、\( \overrightarrow{i_0}=\left ( \begin{array}{c} \cosα_0 \\ \cosα_1 \end{array} \right ) \)
- 座標系 O-X1Y1 からみた ”Y0軸方向の方向余弦” は、\(\overrightarrow{j_0}=\left ( \begin{array}{c} \cosβ_0 \\ cosβ_1 \end{array} \right ) \)
また \(\overrightarrow{i_0} \)、\( \overrightarrow{j_0} \)の大きさは定義から常に1,よってその方向余弦も③と同じ性質をもつ
\( cos^2α_0 + cos^2α_1 = 1 \)、\( cos^2β_0 + cos^2β_1 = 1\) ・・・⑥
行列化: 2x2行列の座標軸変換
さて、次に平面上の任意の点Aのベクトル OA を考える。
その成分は、それぞれの座標系にて
- O-X0Y0 上の \( \small{\overrightarrow{OA}} \) 成分: \( (a_{x0}, a_{y0}) \)
- O-X1Y1 上の \( \small{\overrightarrow{OA}} \) 成分: \( (a_{x1}, a_{y1}) \)
とする。
(同じ点Aを表す) \( \small{\overrightarrow{OA}} \) を O-X0Y0 、O-X1Y1上でそれぞれ表すと、
\( \small{\overrightarrow{OA}} = a_{x0} \cdot \overrightarrow{i_0} + a_{y0} \cdot \overrightarrow{j_0} \)・・・⑦
\( \small{\overrightarrow{OA}}= a_{x1} \cdot \overrightarrow{i_1} + a_{y1} \cdot \overrightarrow{j_1} \)・・・⑧
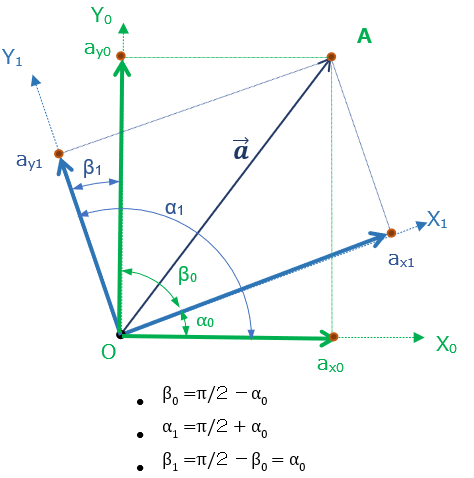
である。さて、⑦式 に i0、j0 (④⑤式)を代入すると
\( \begin{align}
\small{\overrightarrow{OA}} = & \ a_{x0} \cdot \overrightarrow{i_0} + a_{y0} \cdot \overrightarrow{j_0} \\
= & \ a_{x0} \cdot ( cos α_0 \cdot \overrightarrow{i_1} + cos α_1 \cdot \overrightarrow{j_1}) \\
&+ a_{y0} \cdot ( cos β_0 \cdot \overrightarrow{i_1} + cos β_1 \cdot \overrightarrow{j_1})
\end{align} \)
並び替えて
\( \begin{align}
\small{\overrightarrow{OA}} = & \ (a_{x0} \cdot cos α_0 + a_{y0} \cdot cos β_0) \cdot \overrightarrow{i_1} \\
&+ \ (a_{x0} \cdot cos α_1 + a_{y0} \cdot cos β_1) \cdot \overrightarrow{j_1} ・・・⑨
\end{align} \)
同じ \( \small{\overrightarrow{OA}} \) を表している事から、⑧式=⑨式。
つまり、
\( \begin{align}
\small{\overrightarrow{OA}} =& a_{x1} \cdot \overrightarrow{i_1} + a_{y1} \cdot \overrightarrow{j_1} \\
=& \ (a_{x0} \cdot cos α_0 + a_{y0} \cdot cos β_0) \cdot \overrightarrow{i_1} \\
&+ \ (a_{x0} \cdot cos α_1 + a_{y0} \cdot cos β_1) \cdot \overrightarrow{j_1} ・・・⑨
\end{align} \)
\( \overrightarrow{i_1}≠0 、\overrightarrow{j_1}≠0 \) より両辺の係数は等しい。よって
\(a_{x1} = a_{x0} \cdot cos α_0 + a_{y0} \cdot cos β_0 \)
\(a_{y1} = a_{x0} \cdot cos α_1 + a_{y0} \cdot cos β_1 \)
である事がわかる。これを行列で表わして
\(\left ( \begin{array}{c} a_{x1} \\ a_{y1} \end{array} \right ) =\left ( \begin{array}{cc} \cos\alpha_0&\cos\beta_0 \\ \cos\alpha_ 1 & \cos\beta_1 \end{array} \right ) \left ( \begin{array}{c} a_{x0} \\ a_{y0} \end{array} \right ) ・・・⑩ \)
⑩式の 行列部分が、二次元の座標変換 ( <- 回転行列)。
\(R_\alpha =\left ( \begin{array}{cc} \cos\alpha_0&\cos\beta_0 \\ \cos\alpha_ 1 & \cos\beta_1 \end{array} \right ) ・・・⑪ \)
回転行列への展開:二次元(平面)
座標系の回転を示す回転行列
⑪式の角度をα0でまとめる。
座標軸が直行であること、また軸同士の関係から
- \( β_0=\dfrac{\pi}{2} \ – \ α_0 \)
- \( α_1=\dfrac{\pi}{2} + α_0 \)
- \( β_1=\dfrac{\pi}{2} – \ β_0 = α_0 \)
である。

これを使えばRα は、
\( \begin{align}
R_\alpha &=\left ( \begin{array}{cc} \cos\alpha_0&\cos\beta_0 \\ \cos\alpha_ 1 & \cos\beta_1 \end{array} \right ) = \left ( \begin{array}{cc} \cos\alpha_0&\cos ( \displaystyle\frac{\pi}{2}-\alpha_0 ) \\ \cos ( \displaystyle\frac{\pi}{2}+\alpha_0 ) & \cos\alpha_0 \end{array} \right ) \\[8pt]
&= \left ( \begin{array}{cc} \cos\alpha_0&\sin \alpha_0 \\ -\sin \alpha_0 & \cos\alpha_0 \end{array} \right ) ・・・⑫
\end{align} \)
これが 回転角 α0 の回転行列。つまり⑩式は
\(\left ( \begin{array}{c} a_{x1} \\ a_{y1} \end{array} \right ) = \left ( \begin{array}{cc} \cos\alpha_0&\sin \alpha_0 \\ -\sin \alpha_0 & \cos\alpha_0 \end{array} \right ) \left ( \begin{array}{c} a_{x0} \\ a_{y0} \end{array} \right ) ・・・⑬ \)
座標系上の点の回転を示す回転行列
⑬式は座標系を回転させる場合。
座標系は動かずに、点A (ax0 ay0) が原点中心に点B (a`x1 a`y1) へと回転した場合を考える。
視点を変える。
自身が座標軸と一緒に動くと、点Aは相対的に逆方向に動く。つまり、回転している座標系と同時に回転しながら点Aをみていると思えばよい。
(座標軸を+α0 回転と、点Aが-α0 の回転は同じ(視点が違うのみ))
つまり、点Aを α0 回転させる行列 R’α は、⑪式の Rα に -α0 を代入したものとなる。
\( R~’_\alpha = \left ( \begin{array}{cc} \cos(-\alpha_0 ) &\sin(-\alpha_0 ) \\ -\sin (-\alpha_0) & \cos(-\alpha_0) \end{array} \right ) = \left ( \begin{array}{cc} \cos\alpha_0 & – \sin\alpha_0 \\ \sin\alpha_0 & \cos\alpha_0 \end{array} \right ) ・・・⑭ \)
これが、同一座標系上で点を動かすときに使う回転行列である。
⑫式より、こっちの方がよく目にするかも。
これを使うと、 点Aが角度α0回転した点Bの座標は
\(\left ( \begin{array}{c} a’_{x1} \\ a’_{y1} \end{array} \right ) = \left ( \begin{array}{cc} \cos\alpha_0& -\sin \alpha_0 \\ \sin \alpha_0 & \cos\alpha_0 \end{array} \right ) \left ( \begin{array}{c} a_{x0} \\ a_{y0} \end{array} \right ) ・・・⑮\)
で求める事ができる。
二次元の座標変換はここまで、次のページから三次元の座標変換
三次元(空間)での回転行列
三次元(空間)の座標変換、回転行列に入る前に
まず、回転について。
平面上の回転(2次元)の場合、回転の中心は点である。当然傾きはない。
(回転の中心軸は平面に垂直であるという前提条件が含まれているとみてもよい。)
これは、座標軸平面上(XY平面上)で回転が行われる事を意味し(座標平面と回転の平面が一致する)、このおかげで二次元の回転では、回転角 α0の一つで簡単に回転を表現できる。
ところが、3次元上の回転ではそうはいかない。
というのも、二次元と同様に三次元上の実際の回転においても、一つの中心軸周りに一つの回転角で回転するにもかかわらず、その回転の中心軸が必ずしも座標平面と垂直にはならない事が原因。
これにより軸変換はともかく、回転行列にはちょいと細工が必要。
ちなみに、3次元上の回転は、以下の細工が主に使われる。
もちろん変換後の軸の方向余弦を使えば、三次元でも簡単に軸変換は表記可能。オイラー角の入り口となる。
とりあえず、今回は、この入り口までを以下にて。
というのも、平面(2次元の2x2行列 )と同じ流れで軸が一つ増えるだけ。
追記レベルの話。
方向余弦を使った座標変換(3x3行列):三次元(空間)
使用する座標軸
共通の原点Oをもつ二つの座標系 O-X0Y0Z0 と O-X1Y1Z1 を考える。
座標軸も同様に右手右ねじ系とする。
ここで、2次元に対してZ軸が加わるので、その方向の単位ベクトル kn(n=0,1) を追加して、
- X0軸方向、Y0軸方向、Z0軸方向の各単位ベクトル
X0軸方向:\(\overrightarrow{i_0} \) 、Y0軸方向:\(\overrightarrow{j_0} \)、Z0軸方向:\(\overrightarrow{k_0} \) - X1軸方向、Y1軸方向、Z1軸方向の各単位ベクトル
X1軸方向:\(\overrightarrow{i_1} \) 、Y1軸方向:\(\overrightarrow{j_1} \)、Z1軸方向:\(\overrightarrow{k_1} \)
とする。当然この各座標系の\(\overrightarrow{i_n} \) 、\(\overrightarrow{j_n} \)、\(\overrightarrow{k_n} \)(n=0,1)は互いに直行 (つまり正規直行ベクトル)
各軸の方向余弦
\( \small{O-X_0Y_0Z_0} \) から見た \(\small{X_1Y_1Z_1} \) 各軸 の方向余弦
二つの座標系 O-X0Y0Z0 と O-X1Y1Z1 の各軸について 、お互いのなす角を
- X1軸がX0軸 、Y0軸、Z0軸となす角
:α0、β0、γ0 - Y1軸がX0軸 、Y0軸、Z0軸となす角
:α1、β1、γ1 - Z1軸がX0軸 、Y0軸、Z0軸となす角
:α2、β2、γ2
二次元と同様に、この角度を使って i1 、j1、k1 を余弦で表すと
\( \overrightarrow{i_1} = \cos\alpha_0 \cdot \overrightarrow{i_0}+\cos\beta_0 \cdot \overrightarrow{j_0} + \cos\gamma_0 \cdot \overrightarrow{k_0} \)
\( \overrightarrow{j_1} = \cos\alpha_1 \cdot \overrightarrow{i_0}+\cos\beta_1 \cdot \overrightarrow{j_0} + \cos\gamma_1 \cdot \overrightarrow{k_0} \)
\( \overrightarrow{k_1} = \cos\alpha_2 \cdot \overrightarrow{i_0}+\cos\beta_2 \cdot \overrightarrow{j_0} + \cos\gamma_2 \cdot \overrightarrow{k_0} ・・・⑮ \)
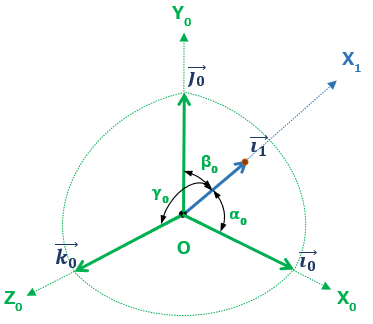
この時方向余弦はそれぞれ、
\( \overrightarrow{i_1} = \small{\left ( \begin{array}{c} \cos{\alpha_0} \\ \cos{\beta_0} \\ \cos{\gamma_0} \end{array} \right )}、 \overrightarrow{j_1} = \small{\left ( \begin{array}{c} \cos{\alpha_1} \\ \cos{\beta_1} \\ \cos{\gamma_1} \end{array} \right )}、 \overrightarrow{k_1} = \small{\left ( \begin{array}{c} \cos{\alpha_2} \\ \cos{\beta_2} \\ \cos{\gamma_2} \end{array} \right )} ・・・⑯ \)
\( \overrightarrow{i_1} \)、\( \overrightarrow{j_1} \)、\( \overrightarrow{k_1} \) は常に大きさ1、角度を任意とすれば、その軌跡は”球”を描く。
つまり、これらの方向余弦は以下の性質をもつ。
\( cos^2α_0+cos^2β_0+cos^2γ_0 = 1 \)
\( cos^2α_1+cos^2β_1+cos^2γ_1 = 1 \)
\( cos^2α_2+cos^2β_2+cos^2γ_2 = 1 \)
\( \small{O-X_1Y_1Z_1 } \) から見た \( \small{X_0Y_0Z_0 }\) 各軸 の方向余弦
逆に、\( O-X_1Y_1Z_1\) から見た \(X_0, Y_0, Z_0 \) 軸を表す。
二次元と同様に 角度を設定しなおせば、
- X0軸が X1軸 、Y1軸、Z1軸となす角
:\(α_0、α_1、α_2\) - Y0軸が X1軸 、Y1軸、Z1軸となす角
:\(β_0、β_1、β_2\) - Z0軸が X1軸 、Y1軸、Z1軸となす角
:\(γ_0、γ_1、γ_2\)
\( \overrightarrow{i_0} \)、\( \overrightarrow{j_0} \)、\( \overrightarrow{k_0} \) は
\( \overrightarrow{i_0} = \cos\alpha_0 \cdot \overrightarrow{i_1}+\cos\alpha_1 \cdot \overrightarrow{j_1} + \cos\alpha_2 \cdot \overrightarrow{k_1} \)
\( \overrightarrow{j_0} = \cos\beta_0 \cdot \overrightarrow{i_1}+\cos\beta_1 \cdot \overrightarrow{j_1} + \cos\beta_2 \cdot \overrightarrow{k_1} \)
\( \overrightarrow{k_0} = \cos\gamma_0 \cdot \overrightarrow{i_1}+\cos\gamma_1 \cdot \overrightarrow{j_1} + \cos\gamma_2 \cdot \overrightarrow{k_1} ・・・⑰ \)
その方向余弦は、
\( \overrightarrow{i_0} = \small{\left ( \begin{array}{c} \cos{\alpha_0} \\ \cos{\alpha_1} \\ \cos{\alpha_2} \end{array} \right )}、 \overrightarrow{j_0} =\small{ \left ( \begin{array}{c} \cos{\beta_0} \\ \cos{\beta_1} \\ \cos{\beta_2} \end{array} \right )}、 \overrightarrow{k_0} = \small{\left ( \begin{array}{c} \cos{\gamma_0} \\ \cos{\gamma_1} \\ \cos{\gamma_2} \end{array} \right ) }・・・⑱ \)
同様に
\( cos^2α_0+cos^2α_1+cos^2α_2 = 1 \)
\( cos^2β_0+cos^2β_1+cos^2β_2 = 1 \)
\( cos^2γ_0+cos^2γ_1+cos^2γ_2 = 1 \)
の性質ももつ。
行列化 : 3x3行列の座標軸変換
以下、これも二次元と同様の流れ。
つまり、空間上の任意の点Aに対して原点Oを始点に持つベクトル \( \small{\overrightarrow{OA}} \) を考える。
- O-X0Y0Z0上の \( \small{\overrightarrow{OA}} \) 成分:\( ( a_{x0} \ , \ a_{y0} \ , \ a_{z0} ) \)
- O-X1Y1Z1上の \( \small{\overrightarrow{OA}} \) 成分:\( (a_{x1} \ , \ a_{y1} \ , \ a_{z1}) \)
とする。点Aは同じ、つまり
\( \small{\overrightarrow{OA}} = a_{x0} \cdot \overrightarrow{i_0}+a_{y0} \cdot \overrightarrow{j_0}+a_{z0} \cdot \overrightarrow{k_0} \)・・・⑲
\( \small{\overrightarrow{OA}} = a_{x1} \cdot \overrightarrow{i_1}+a_{y1} \cdot \overrightarrow{j_1}+a_{z1} \cdot \overrightarrow{k_1}\)・・・⑳
二次元と同じ式展開で⑲式の \( \overrightarrow{i_0} \) , \( \overrightarrow{j_0} \) , \( \overrightarrow{k_0} \) を⑰式で置き換える
\( \begin{align}
\small{\overrightarrow{OA}} =& a_{x0} \cdot \overrightarrow{i_0} + a_{y0} \cdot \overrightarrow{j_0} + a_{z0} \cdot \overrightarrow{k_0}\\
= & \ a_{x0} \cdot ( cos α_0 \cdot \overrightarrow{i_1} + cos α_1 \cdot \overrightarrow{j_1}+cos α_2 \cdot \overrightarrow{k_1}) \\
&+ a_{y0} \cdot ( cos β_0 \cdot \overrightarrow{i_1} + cos β_1 \cdot \overrightarrow{j_1}+ cos β_2 \cdot \overrightarrow{k_1}) \\
&+ a_{z0} \cdot ( cos γ_0 \cdot \overrightarrow{i_1} + cos γ_1 \cdot \overrightarrow{j_1}+ cos γ_2 \cdot \overrightarrow{k_1}) \\
=& \ (a_{x0} \cdot cos α_0 + a_{y0} \cdot cos β_0+ a_{z0} \cdot cos γ_0) \cdot \overrightarrow{i_1} \\
&+ \ (a_{x0} \cdot cos α_1 + a_{y0} \cdot cos β_1+ a_{z0} \cdot cos γ_1) \cdot \overrightarrow{j_1} \\
&+ \ (a_{x0} \cdot cos α_2 + a_{y0} \cdot cos β_2+ a_{z0} \cdot cos γ_2) \cdot \overrightarrow{k_1}・・・㉑
\end{align} \)
㉑式が⑳式と同一 (点Aが同一より)。
\( \begin{align}
\small{\overrightarrow{OA}} =& a_{x1} \cdot \overrightarrow{i_1}+a_{y1} \cdot \overrightarrow{j_1}+a_{z1} \cdot \overrightarrow{k_1} \\
=& \ (a_{x0} \cdot cos α_0 + a_{y0} \cdot cos β_0+ a_{z0} \cdot cos γ_0) \cdot \overrightarrow{i_1} \\
&+ \ (a_{x0} \cdot cos α_1 + a_{y0} \cdot cos β_1+ a_{z0} \cdot cos γ_1) \cdot \overrightarrow{j_1} \\
&+ \ (a_{x0} \cdot cos α_2 + a_{y0} \cdot cos β_2+ a_{z0} \cdot cos γ_2) \cdot \overrightarrow{k_1}
\end{align} \)
各係数を比較すれば、
\( a_{x1}=a_{x0}・cosα_0+a_{y0}・cosβ_0+a_{z0}・cosγ_0 \)
\( a_{y1}=a_{x0}・cosα_1+a_{y0}・cosβ_1+a_{z0}・cosγ_1 \)
\( a_{z1}=a_{x0}・cosα_2+a_{y0}・cosβ_2+a_{z0}・cosγ_2 \)
これを行列化
\( \left( \begin{array}{c} a_{x1} \\ a_{y1} \\ a_{z1} \end{array} \right )
= \left ( \begin{array}{ccc}
\cos\alpha_0 & \cos\beta_0 & cos\gamma_0 \\
\cos\alpha_1 & \cos\beta_1 & cos\gamma_1 \\
\cos\alpha_2 & \cos\beta_2 & cos\gamma_2
\end{array} \right )
\left ( \begin{array}{c}
a_{x0} \\ a_{y0} \\ a_{z0}
\end{array} \right ) ・・・㉒ \)
この行列部分
\(R = \left( \begin{array}{ccc}
\cos\alpha_0 & \cos\beta_0 & cos\gamma_0 \\
\cos\alpha_1 & \cos\beta_1 & cos\gamma_1 \\
\cos\alpha_2 & \cos\beta_2 & cos\gamma_2
\end{array} \right ) ・・・㉓ \)
が3次元の座標変換を行う行列。2次元と同様に変換後の各軸の方向余弦が行ベクトルで並ぶ。
回転行列への展開:三次元(空間)
一つの座標軸を中心に座標系を回転させる時の回転行列
㉒式の行列 R の各行ベクトルは、上から順に変換後の X1->Y1->Z1 軸の方向余弦
Z軸廻りのψ回転
まず、Z軸廻りに ψ回転 させる。
1行目の方向余弦の角度α0、β0、γ0は、定義より変換前のX0軸 、Y0軸 、Z0軸と変換後のX1軸のなす角となる(図4)。つまり、
\( \alpha_0=\psi \)、\( \beta_0=\displaystyle\frac{\pi}{2}-\psi \)、\( \gamma_0=\displaystyle\frac{\pi}{2} \)
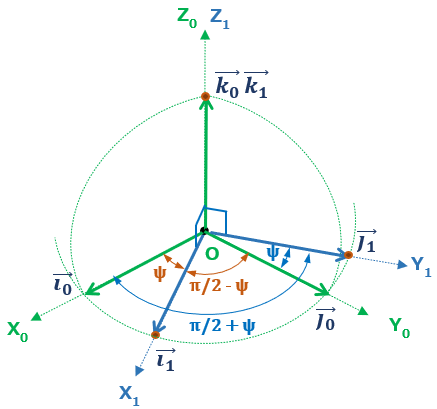
同様に、2行目の行ベクトル(Y1軸となす角)は
\( \alpha_1=\displaystyle\frac{\pi}{2}+\psi \)、\( \beta_1=\psi \)、\( \gamma_1=\displaystyle\frac{\pi}{2} \)
3行目の行ベクトル (Z1軸となす角)は、
\( \alpha_2=\displaystyle\frac{\pi}{2} \)、\( \beta_2=\displaystyle\frac{\pi}{2} \)、\( \gamma_2=0 \)
この時の回転行列を Rψ とすれば
\(\begin{align}
R_\psi &= \left( \begin{array}{ccc}
\cos\alpha_0 & \cos\beta_0 & cos\gamma_0 \\
\cos\alpha_1 & \cos\beta_1 & cos\gamma_1 \\
\cos\alpha_2 & \cos\beta_2 & cos\gamma_2
\end{array} \right )
= \left( \begin{array}{ccc}
\cos\psi & \cos(\displaystyle\frac{\pi}{2}-\psi ) & cos\displaystyle\frac{\pi}{2} \\
\cos(\displaystyle\frac{\pi}{2}+\psi) & \cos\psi & cos\displaystyle\frac{\pi}{2} \\
\cos\displaystyle\frac{\pi}{2} & \cos\displaystyle\frac{\pi}{2} & cos 0
\end{array} \right ) \\[8pt]
&=\left( \begin{array}{ccc}
\cos\psi & \sin\psi & 0 \\
-\sin\psi & \cos\psi & 0 \\
0 & 0 & 1
\end{array} \right ) ・・・㉔
\end{align} \)
そのまま続いてY軸廻り、X軸廻り。
Y軸廻りのθ回転
Y軸廻りに θ回転させる回転行列 Rθ は Rψ と同様に算出すれば(図5)

\(\begin{align}
R_\theta &= \left( \begin{array}{ccc}
\cos\alpha_0 & \cos\beta_0 & cos\gamma_0 \\
\cos\alpha_1 & \cos\beta_1 & cos\gamma_1 \\
\cos\alpha_2 & \cos\beta_2 & cos\gamma_2
\end{array} \right )
= \left( \begin{array}{ccc}
\cos\theta & cos\displaystyle\frac{\pi}{2} & \cos(\displaystyle\frac{\pi}{2}+\theta )\\
\cos\displaystyle\frac{\pi}{2} & cos 0 & \cos\displaystyle\frac{\pi}{2}\\
\cos(\displaystyle\frac{\pi}{2}- \theta) & cos\displaystyle\frac{\pi}{2} & \cos\theta
\end{array} \right ) \\[8pt]
&= \left( \begin{array}{ccc}
\cos\theta & 0 & -\sin\theta \\
0 & 1 & 0 \\
\sin\theta & 0 & \cos\theta
\end{array} \right ) ・・・㉕
\end{align} \)
X軸廻りのφ回転
X軸廻りに φ回転させる回転行列 Rφ も Rψ と同様に求めれば(図6)

\(\begin{align}
R_\phi &= \left( \begin{array}{ccc}
\cos\alpha_0 & \cos\beta_0 & cos\gamma_0 \\
\cos\alpha_1 & \cos\beta_1 & cos\gamma_1 \\
\cos\alpha_2 & \cos\beta_2 & cos\gamma_2
\end{array} \right )
= \left( \begin{array}{ccc}
cos 0 &\cos\displaystyle\frac{\pi}{2} & \cos\displaystyle\frac{\pi}{2}\\
cos\displaystyle\frac{\pi}{2} &\cos\phi & \cos(\displaystyle\frac{\pi}{2}-\phi )\\
cos\displaystyle\frac{\pi}{2} &\cos(\displaystyle\frac{\pi}{2}+\phi) & \cos\phi
\end{array} \right ) \\[8pt]
&= \left( \begin{array}{ccc}
1 & 0 & 0 \\
0 &\cos\phi & \sin\phi \\
0 & -\sin\phi & \cos\phi
\end{array} \right )・・・㉖
\end{align} \)
この㉔、㉕、㉖式が、オイラー角へ続く。

