はじめに
前回の記事内で、行列の積の成分計算は
- 行ベクトルと列ベクトルの内積計算
と同じであると(こちら)
これを利用すると、行列の積の計算に内積の特長が利用できる。
これが、行列を使った軸変換のキモ。回転行列は軸変換の一部(=限定版)。
(内積?投影長?については、以下の記事にて)
- 2軸に対して行うのであれば、2つの行ベクトル(つまり2x2行列)、
- 3軸に対して行うのであれば、3つの行ベクトル(つまり3x3行列)、
- n個の軸に対して行うのであればn個の行ベクトル(つまりnxn行列)
を用意すれば、その数の軸変換ができる。その流れを以下に。
ベクトルの内積を使用した行列による軸変換
あらためて
”正規ベクトルの行ベクトル(大きさ”1”)で構成される行列” と ”任意の列ベクトル” の行列の積で考える。
ベクトルの内積の意味をふまえると、この場合の行列の積の成分計算結果は、行ベクトル側は大きさ1なので
”列ベクトルの長さを、行ベクトル方向に投影した長さ” が算出される。
\( \begin{align}
\overrightarrow{OA}・\overrightarrow{OB} &= |\overrightarrow{OA}|・|\overrightarrow{OB}|cosθ \\[6pt]
&=|\overrightarrow{OB}|cosθ \ (∵ |\overrightarrow{OA}|=1) \end{align} \)
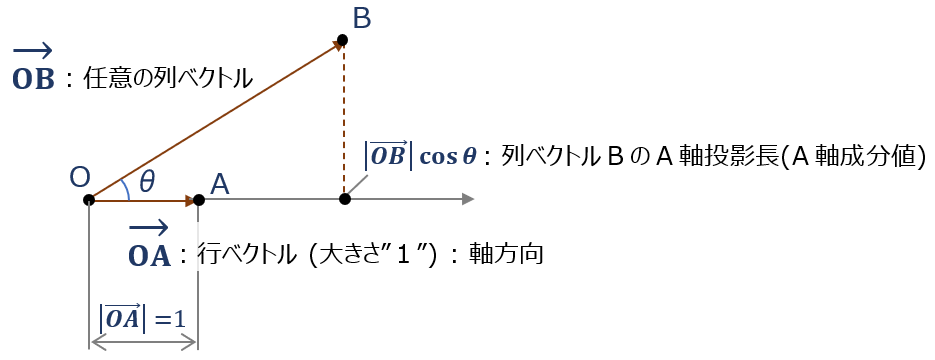
これが座標値算出の(仕組みの)ベース。
1次元ではただのベクトル内積計算になるので、具体的な例として、2次元(2×2行列)から始める。つまり2軸の軸変換。
(あとは3次元でもn次元でも何軸でも軸変換のやり方は同じ。)
ちなみにこの任意軸への座標軸変換は、応用で座標系を回転させる回転行列(オイラー角)へと続く。
まずは任意の軸への座標軸変換から
任意の軸への座標変換
任意方向の軸の設定
まずは基準の座標系 O-XY。この座標系O-XYは、原点Oを通り直行するX軸 Y軸をもつ座標系。
X軸、Y軸 の方向の単位ベクトルは
- \(\overrightarrow{i} \): X軸の方向の単位ベクトル
- \(\overrightarrow{j} \): Y軸の方向の単位ベクトル
とする。
(\(\overrightarrow{i} \) 、\(\overrightarrow{j} \)は O-XY上の正規直行基底)
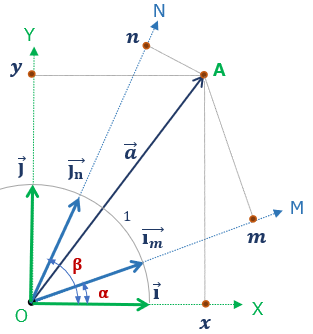
ここに、O-XY上に新たな任意の2軸を追加(M軸とN軸:方向は任意、原点Oは共有、)
<- ここでは、まずは任意方向の軸でためして、変換の仕組みの確認
(よって直行でなくても可)
さて、これを O-MNとして設定。
このM軸、N軸 の方向を
- \(\overrightarrow{i_m}= (x_m , y_m) \) : M軸の方向ベクトル (単位ベクトル: \( {x_m}^2+{y_m}^2=1 \) )
- \(\overrightarrow{j_n}= (x_n , y_n) \) : N軸の方向ベクトル (単位ベクトル:\( {x_n}^2+{y_n}^2=1 \) )
にて定義し、あわせてX軸とM軸のなす角をα、 X軸とN軸のなす角をβとし、これらのベクトルをO-XY座標系で成分表示すれば
- \(\overrightarrow{i_m}= (x_m , y_m) = (\cos\alpha , \cos(\displaystyle\frac{π}{2}-\alpha))= (\cos\alpha , \sin\alpha) \)
- \(\overrightarrow{j_n}= (x_n , y_n) = (\cos\beta , \cos(\displaystyle\frac{π}{2}-\beta)) = (\cos\beta , \sin\beta) \)
ちなみに、\(\overrightarrow{i_m}\)、\(\overrightarrow{j_n}\) は単位ベクトル、原店Oを基点かつ方向が任意である事を踏まえれば、これらのM軸、N軸の方向を示す各ベクトルは原点Oを中心としたr=1の円。
任意の軸への座標変換
さてこれを踏まえ軸変換。X軸->M軸 、 Y軸 ->N軸への変換を考える。
平面上に点Aを設定する。
O-XY上の点Aの座標は \( \left ( \begin{array}{c} x \\y \end{array} \right ) \) とし、原点Oから点Aへのベクトルを \( \small{\overrightarrow{ OA }}=\normalsize{\overrightarrow{a}} \)とする。
次に、O-MN上での点Aの座標を \( \left ( \begin{array}{c} m \\n \end{array} \right ) \)とすれば、\( \left ( \begin{array}{c} m \\n \end{array} \right ) \) は、\(\overrightarrow{a} \)のM軸 N軸への投影成分である事から、前述のベクトルの内積の性質を使い、
\( \begin{align}
m &= \overrightarrow{i_m} \cdot \overrightarrow{a} \\
&=\cos\alpha\cdot x + \sin\alpha\cdot y
\end{align} \)
\( \begin{align}
n &= \overrightarrow{j_n} \cdot \overrightarrow{a} \\
&=\cos\beta\cdot x + \sin\beta\cdot y
\end{align} \)
となる。
これを行列化する。つまり、任意の軸への投影成分は以下の
\( \begin{align}
m &=\cos\alpha\cdot x + \sin\alpha\cdot y \\
n &=\cos\beta\cdot x + \sin\beta\cdot y
\end{align} \)
を使い、行列として式にあらわせば
\( \normalsize{\left ( \begin{array}{c}
m\\n\end{array} \right )
=\left ( \begin{array}{cc}
\cos\alpha&\sin\alpha \\
\cos\beta&\sin\beta \end{array}\right)
\left ( \begin{array}{c}
x\\y \end{array}\right) } \) ・・・①
と表現できる。これが任意の軸への投影。
任意の軸への軸変換行列の見方
改めてベクトルの内積計算が投影である事をふまえ①式を見れば、軸変換は
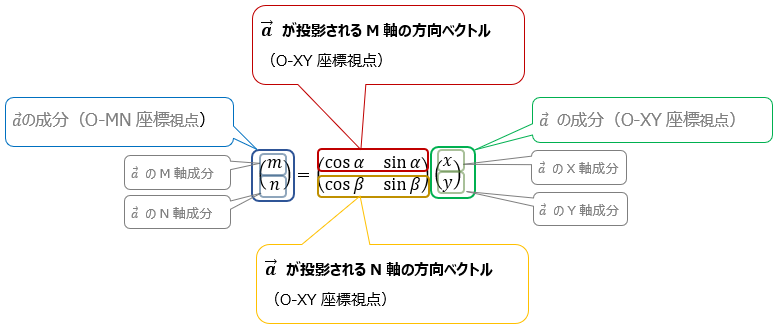
の行列で可能である事がわかる。この見方を頭の片隅にいれておく。
行列の行数/列数が増えても見方は同じ。
この座標軸変換が回転行列の入り口。というか、この座標軸変換ができる特徴をを使って、変換後の座標軸が元の座標に対して一定角回転するように変換したものが回転行列。
(ざっくり言えば、行ベクトルが全て単位ベクトル(内積による変換後の軸の値がそのまま新しい軸の座標値)、かつ行ベクトル同士が直行ベクトル(変換後の座標軸も直行)であれば、回転行列になる)
もう少し回転行列の詳細を。。
直行軸への座標変換 (回転行列)
次に、変換後の任意の2軸(M軸とN軸)に
”変換前の2軸(X軸Y軸)と同じ原点を共有し、かつ位置関係、直行関係をそのまま保つ”
という制限を加える。
つまり、変換前の座標系を、原点O中心に丸ごと回転させる変換となる。
直交座標軸の設定
変換前の座標軸O-X0Y0は上述と同じ設定。
-> 原点Oを通り、直行するX0Y0軸をもつ座標系。
座標軸は右手系で設定、角度はX→Y方向を正
変換後の座標系をO-X1Y1とし、O-X1Y1も右手系
かつ、”X1軸 Y1軸も直行関係である”、の制限を加える。
つまり、座標系は右手系を保ち軸の配置に変更はしない(角度の正負方向も同じ)
前回同様、平面上に点Aを設定する。
原点Oを始点に点A結ぶベクトルを \( \normalsize{\overrightarrow{a}} \)とし、
O-X0Y0 上の点Aの座標を \( \left ( \begin{array}{c} x_0 \\y_0 \end{array} \right ) \) \( \\[2pt] \) O-X1Y1 上の点Aの座標を\( \left ( \begin{array}{c} x_1 \\y_1 \end{array} \right ) \)
とする(図②)
直行軸への軸変換行列 (回転行列)
変換される軸は X0軸-> X1軸 、 Y0軸 -> Y1軸 である。
O-X1Y1 ではX1軸Y1軸の関係はO-X0Y0の関係を保つので、αが決まれば、①式のβも自動的にきまる。
つまり
\(\beta= \alpha+\displaystyle\frac{π}{2} \)・・・②
これを前ページの①式に代入すれば
\( \begin{align}
\left ( \begin{array}{c}
x_1\\y_1 \end{array} \right )
& = \left ( \begin{array}{cc}
\cos\alpha & \sin\alpha \\
\cos\beta & \sin\beta \end{array}\right)
\left ( \begin{array}{c}
x_0\\y_0 \end{array}\right) \\[8pt]
&= \left ( \begin{array}{cc}
\cos\alpha & \sin\alpha \\
\cos(\alpha+\displaystyle\frac{π}{2}) & \sin(\alpha+\displaystyle\frac{π}{2}) \end{array}\right)
\left ( \begin{array}{c}
x_0\\y_0 \end{array}\right) \\[8pt]
& = \left ( \begin{array}{cc}
\cos\alpha & \sin\alpha \\
-\sin\alpha & \cos\alpha \end{array}\right)
\left ( \begin{array}{c}
x_0\\y_0 \end{array}\right) ・・・③
\end{align} \)
これが回転行列。
(当然ではあるが、一つの回転角αで変換前後の座標値の関係を示す事ができる)
直行軸への軸変換行列の見方 (回転行列)
この行列の見方は軸変換の場合と同じである。
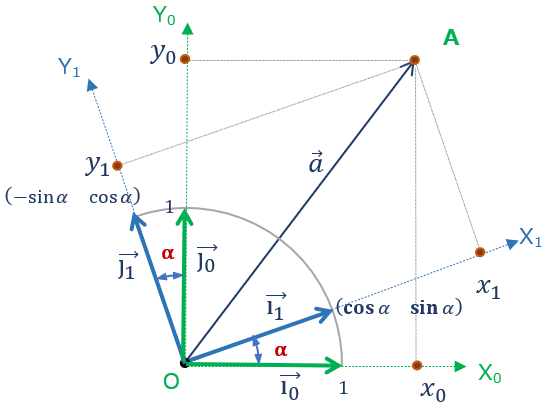
Ra において、1行目を抜き出した \( (\cos\alpha \sin\alpha) \) を \(\overrightarrow{i_1} \)、2行目を抜き出した \( (-\sin\alpha \cos\alpha) \) を \(\overrightarrow{j_1} \)とみれば、これらの行ベクトルは変換後の軸の方向である。
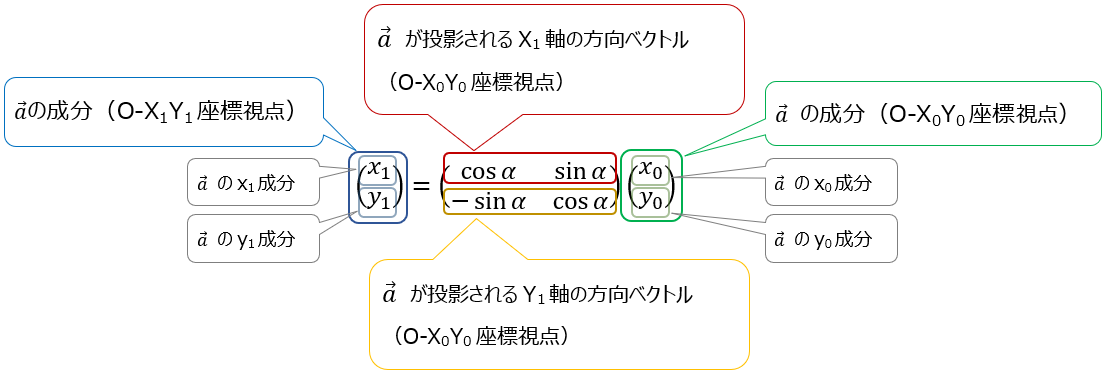
つまり、行列内の各行ベクトルは変換後の軸の方向を示す。
また回転しただけなので当然\(\overrightarrow{i_1} \)、\(\overrightarrow{j_1} \)もその平面上での正規直行基底(大きさ1&互いに直行)
追記
ベクトルの内積を用いた軸変換から回転行列へと展開したが、回転行列については、方向余弦を用いた導入の方がわかりやすいかも。。以下の記事にて。



