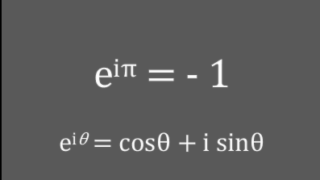世界で最も美しい公式：オイラーの公式

オイラーの公式 : Euler’s Fomula

世界で最も美しいといわれる式

\( e^{i \pi}=-1 \) ・・・①

この式は、オイラーの公式

\( e^{i \theta}=cos \theta + i \cdot sin \theta \) ・・・②

から導かれる（②式の \(\theta \) に \( \pi \) を代入すると①式）。

振動系の解析では、方程式の一般解としてこの形が出てくるで、中身は知らなくてもこの形は覚えておいたよいかな。

理論物理学者のファインマン博士は、この式を ”宝石” と呼んだ。

今回は美しいと言われている理由とその使い方を少し。”美しい公式だね” だけでは、ちょっともったいないしね

美しいと言われる理由について

①式＆②式の登場人物は（使用されている数学の要素は）、

ネイピア数 ” e “
虚数 ” i “
円周率 ” π “
負の世界 ” – “
指数関数
三角関数

着目するのは、この式の成り立ちである。

この式の登場人物（各要素）は数学の歴史上、それぞれ別の時代 / 別の地域 / 別の定義のモノ。

つまり各々別の必要性（動機）があり、定義されてきたものであるという事。

周期関数である三角関数、非周期関数である指数関数、実数と虚数からなる複素数、マイナスの世界、何度微分しても形を変えない指数関数e^xの底となるネイピア数e、円周率πと、一見すると全く別物なのである。

この各世界を、ひとつの世界に集約（統合）するのが②式のオイラーの公式。

この統合が成り立つ事（つじつまがすっきりと合う事）は、統合した世界においてのみならず、それまでの各世界での論理構築が”真”であった事の裏づけにもなっているのである。

-> ”世界で最も美しい公式”と呼ばれる理由である。

300年もの前（Leonhard Euler (1707 – 1783)）の話である。

オイラー先生曰く

純粋数学と呼び慣わされているような分野においてまで、観察を重要視するのは、少なからず逆説的に聞こえよう。・・・しかしながら・・・今日知られている数の性質は、大部分が観察によって明るみに出たものである。
また、それらが真実であることは、厳密な証明によって確かめられるよりもずっと前に分かっていたのである。

しかし、”ずっと前に分かっていたのである”って、カッコいい。すでに存在をしていて、見つけられるべくして、見つけたモノ。

数学は神様と会話ができる言語っていう人がいるのもわからないでもない。。

図形的に解釈

さて、実を言うとオイラーの公式は図で書くと、その解釈はそれ程難しくはない。

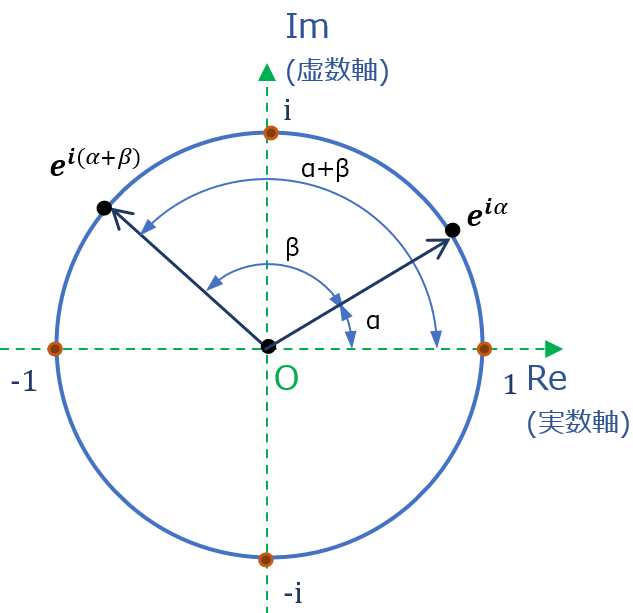
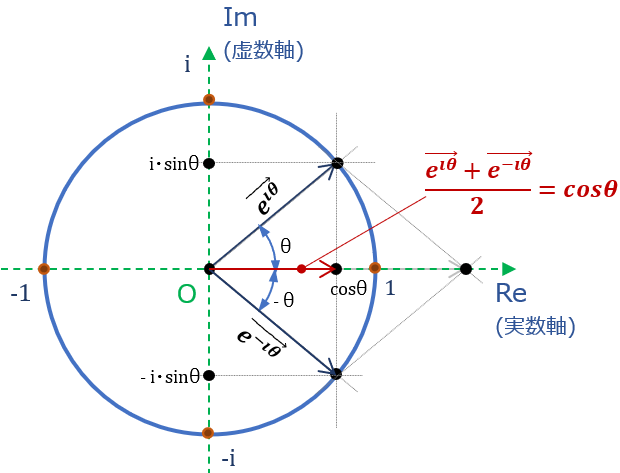
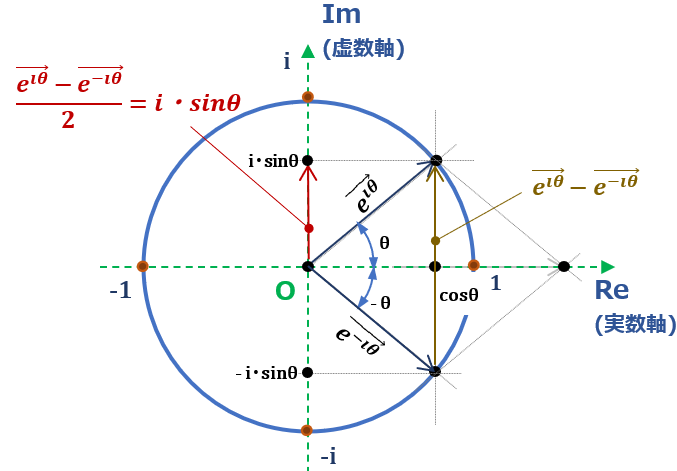
②式の右辺 (\( cos θ + i \cdot sin θ \)) に着目すれば、これは、複素数表示 \( \small{Z} = \small{Re} + i\cdot \small{Im} \) ( \( \small{Re} \):実数部、\( \small{Im} \)：虚数部) を使った、複素平面（ガウス平面）の半径１の円（変数 \( θ \)) である事は明らか。← これが\( e^{i θ} \) の中身

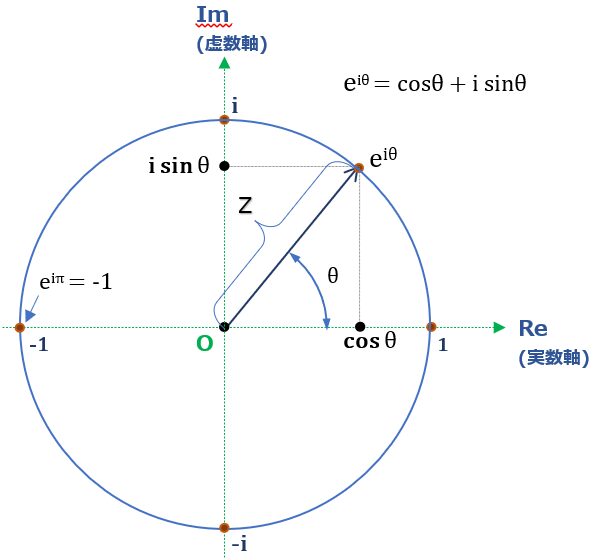
\( \small{Z}= e^{i θ} = cos θ + i \cdot sin θ \)

つまり単に、複素平面上にて\( e^{i θ} \) は単位円を示している、と言っているにすぎない。

\( e^{i θ} \) は、

\( e^{i θ} \) は実数部に \( cosθ \)、虚数部 \( i \) に \( sinθ \) をもつ複素数
\( θ \) の変化に伴い、複素平面にて \( e^{i θ} \) の軌跡は単位１の円を描く
(複素平面：横軸 – 実数軸、縦軸 – 虚数軸 )

これが \( e^{i θ}=cos θ + i \cdot sin θ \) の図形的な解釈。

（指数関数である \( e^{i θ} \) は複素平面でみれば、単位１の円をぐるぐるとまわっているのである <- 実数軸への投影した点の動きをイメージすると、サインカーブ等で見られる波型の動きをする。三角関数で置き換えられるイメージはココでわかるかと）

ちなみに、\( e^{i θ} \) が描く円において、\( (θ =\pi) \) の時が”最も美しい式”と言われる ①式を表す点。

\( e^{i \pi} = – 1 \) \( (θ =\pi) \)

当たり前だが、ちゃんと実数軸上の点になっている。

実数平面（\( XY \) 平面)にて、\(\vec{r}= cos θ \cdot \vec{i} + sin θ \cdot \vec{j} \) が、半径”1”の円を描くのと同じイメージ

（ \( \vec{i} \) = (1,0)、\( \vec{j} \) = (0,1) は \( XY \) 平面の正規直行基底）

さて、\( e^{i θ} \) が \( cos θ + i \cdot sin θ \) と等しくなる事の証明もなかなか面白い。むずかしいパズルが解けた時のようなすっきり感が味わえる（オイラー先生、スゴし）。

以下の記事にて

さてさて、このオイラーの公式、美しい公式だね、、、から、ちょっとだけ先へ。使われ方ちょっと知っておくと、視野が広がっていく。なにせ、世界統合する数式。いろいろなトコロでちょこちょこ顔を出す。

まずは簡単なところから。

公式の利用もこんな感じで

利用その①：正弦、余弦の加法定理が出てくる

指数の計算規則と虚数の定義 \( ( i^2 = -1) \) を使うと、三角関数の加法定理の導入に使える

加法定理は、確か高校(？)の頃の教科書ではいきなり出てきて、サイン・コス・コス・サインみたいな呪文で覚えさせられた記憶があるが、②式を知ってれば、覚える必要はない。

<三角関数の加法定理>

オイラーの公式（\( e^{i θ}=cos θ + i \cdot sin θ \)）を使えば、\( e^{i(α+β)} \) は

\( e^{i(α+β)} = cos(α+β) + i \cdot sin(α+β) \) ・・・③

（複素平面上にてこの角度の足し算をみれば以下（下図））

また、

\( \begin{align}
e^{i(α+β)} &= e^{iα} \cdot e^{iβ} \\[8pt]
&= (cosα+ i \cdot sinα) (cosβ+ i \cdot sinβ) \\[8pt]
&= (cosα \cdot cosβ \ + \ i^2 \cdot sinα \cdot sinβ ) \ + \ i \cdot ( sinα \cdot cosβ \ + \ cosα \cdot sinβ) \\[8pt]
&= (cosα \cdot cosβ \ – \ sinα \cdot sinβ ) \ + \ i \cdot ( sinα \cdot cosβ \ + \ cosα \cdot sinβ)・・・④ \\
\end{align} \)

ここで、③式と④式を比較すれば、

\( \begin{align}
& cos(α+β) + i \cdot sin(α+β) \\[8pt]
&= (cosα \cdot cosβ \ – \ sinα \cdot sinβ ) \ + \ i \cdot ( sinα \cdot cosβ \ + \ cosα \cdot sinβ) \end{align} \)

この式の実数部、虚数部は各々等しいという事から、三角関数の加法定理が導かれる。

\( cos(α+β) = cosα \cdot cosβ \ – \ sinα \cdot sinβ \) ・・・⑤

\( sin(α+β) = sinα \cdot cosβ \ + \ cosα \cdot sinβ \) ・・・⑥

正弦、余弦の加法定理はオイラーの公式から同時に計算される。(ちなみに、(α‐β)も同じ計算方法）

この方法は、倍角の公式であろうが、3つの角の加法計算であろうが利用できる。

利用その②：三角関数が指数関数への置き換えられる

振動系の計算でよく使用される三角関数から指数関数への置き換え

オイラーの公式から

\( \begin{align} e^{iθ} &=cosθ + i \cdot sinθ ・・・② \\[8pt]
e^{-iθ} & =cos(-θ) + i \cdot sin(-θ) \\[4pt]
&=cosθ \ – \ i \cdot sinθ ・・・⑦ \end{align} \)

この2つを使えば、三角関数を指数関数に置き換え可能

<\( cosθ \)>

\( cosθ \) は、(② + ⑦) / 2 を計算すれば

\( cosθ = \dfrac{e^{iθ} + e^{-iθ}}{2} \)・・・⑧

これは、図的に考えれば当たり前で、\( e^{iθ} \)の点の動きと逆方向に動く\( e^{-iθ} \)を頂点にもつ原点O基準の二つの複素ベクトルを足せば、その合成ベクトルは必ず実数軸上。その合成ベクトルを２で割れば（\( e^{±iθ} \) の実数軸成分である）cosθとなるため、容易にcosθが抜き出せる。
（下図参照）

<\( sinθ \)>

\( sinθ \) は、(② – ⑦) / 2 を計算すれば、

\( sinθ = \dfrac{e^{iθ} \ – \ e^{-iθ}}{2i} \) ・・・⑨

こっちも複素ベクトルで考えれば、すぐにイメージできる
(下図参照)

ちなみに、⑧⑨式は、微分が必要な時に威力を発揮する（\( e^{θ} \) は何度微分しても変わらないため）。

振動等の計算式で \( e^{iθ} \) とか出てくると、うぇっ！と拒絶モードに入りそうになるが、恐れずに足らず。実はただの三角関数。ハードルはぐっと下がる（はず）。

利用その③： xのn乗=1 の方程式の解も作図で答えがでる

さて、 \( e^{iθ} \) が複素平面上の単位円をぐるぐる回るっていうイメージを補完するために一例を。

方程式

\( x^{n}=1 （n = 1,2,3・・・）\) ・・・⑩

にオイラーの公式を使ってみる。図解的解釈をすると、解は一発で見てわかる。

というのも、複素数平面上で、頂点の一つに \( x=1 \) を持つ正ｎ角形を書いた時に、その他の頂点が \( x^{n}=1 \) の解となるためである。

以下に解説

概要解説

まずこの方程式の \(ｘ\) を \( x=e^{iφ} \) とおくと⑩式は

\( e^{iφ \cdot n} = 1（n = 1,2,3・・・）\) ・・・⑪

となる。つまり、\(φ \) がわかれば \( x \) がわかる。

さてここで、オイラーの公式 \( e^{iφ}=cosφ + i \cdot sinφ \) が示す複素平面の円を使う

この公式の \(φ \) の解が ”= 1” となるのは ( \( cosφ + i \cdot sinφ = 1 \) )、\(φ = 2\pi \) の点を示す時。
(整数倍も含めれば、\( φ =2 \pi k (k=1,2・・・ ) \) )

つまり

\( e^{i \cdot 2\pi \cdot k} = 1 \ (k=1,2・・・) \) ・・・⑫

である。

つまり⑪式⑫式から、\( e^{i(nφ)} = e^{i (2\pi k)} \)

これから、\( nφ \) が、\( nφ =2 \pi k \)（k=1,2・・・）を満たすとき⑫式の解となる。これを変形して

\( φ =\dfrac{2 \pi}{n}k \)

角度 \( φ \) は、\( 2\pi \) を \(n \) 等分した角度の整数倍である事がわかる。

先に答えをかけば、

\( x=e^{iφ} \) とした時 \( x^{n}=1 \ (n = 1,2,3・・・) \) の一般解は、

複素数平面上の円”\( e^{iφ} \) ” 上において \( φ =\dfrac{2 \pi}{n}k \) が示す点

つまり

\( x=e^{iφ} =cos\dfrac{2 \pi}{n}k + i \cdot sin\dfrac{2 \pi}{n}k \)

が答え。

また \( k \) は、\( k ≦ n \) ( \( φ≦２\pi \)) までで十分
（それ以上はぐるぐる回って、既出の点（解）を順に示すだけ。）

図で書いた方がわかりやすい。以下にて

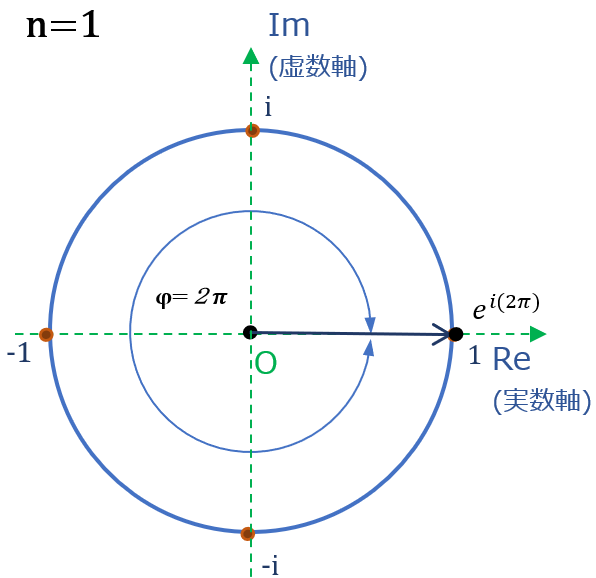
n=1の場合（ \( x^1=1 \) の解）

方程式は \( x^{1}=1 \)

解をもつときの \(φ \) は \( φ =2 \pi \)

言うまでもないが、解は \( x =1 \)

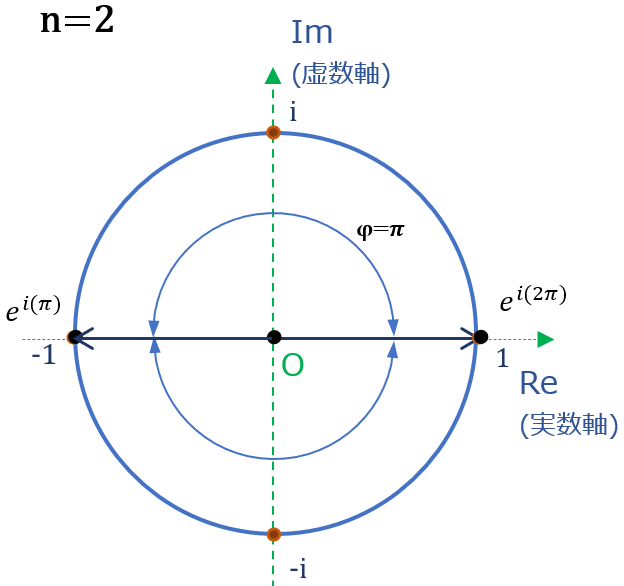
n=2の場合（ \( x^2=1 \) の解）

方程式は \( x^{2}=1 \)、 \( e^{iφ} \)の円上の点が方程式の解である事を踏まえ、

\( n=2 \) より、円を2等分した点が解。

つまり \( φ = \pi、2 \pi \)（解を示す点は実数軸上）
(\( φ =\dfrac{2 \pi}{n}k、n=2 \) より \( φ =\pi k \)、\( k≦ n \) より k=1.2)

オイラーの公式を使えば解は

\( x= e^{i\pi} = cos \pi + i \cdot sin \pi = -1 \)
\( x= e^{i 2\pi} = cos 2\pi + i \cdot sin 2\pi = 1 \)

の二つ。

このあたりまでは、単純に因数分解を使って、\( x^2-1=(x+1)(x-1)=0 \) より \( x=±1 \)とした方が早い。

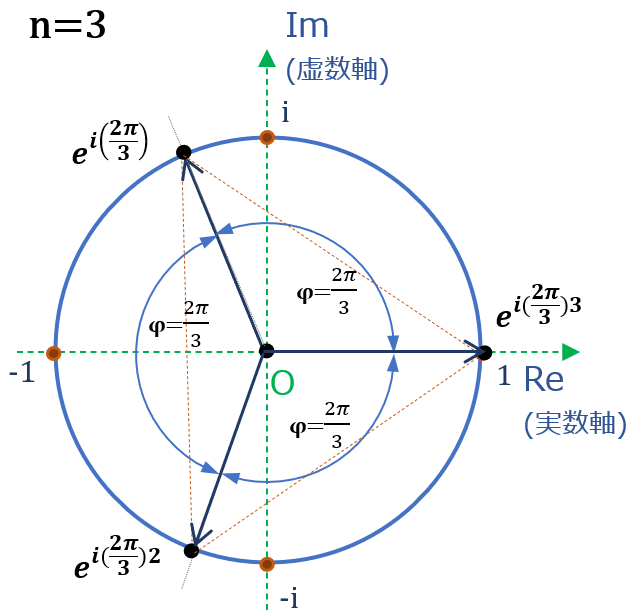
n=3の場合（ \( x^3=1 \) の解）

方程式は \( x^{3}=1 \)、図からみれば、複素平面の実数軸上の”１”を基準にした正三角形の各点が解

n=3を踏まえれば、\( e^{iφ} \) の円を3等分した点、つまり

\( φ =\dfrac{2\pi}{3}, \dfrac{4\pi}{3}, 2\pi \)における円上の点が方程式の解

（\( φ =\dfrac{2 \pi}{n}k、n=3 \) より \( φ =\dfrac{2\pi}{3} k \)、\( k≦ n \) より k=1,2,3)

オイラーの公式を使えば解は、

\( x= e^{i \cdot \frac{2 \pi}{3}} = cos \dfrac{2 \pi}{3} + i \cdot sin \dfrac{2 \pi}{3} = – \dfrac{1}{2} + \dfrac{\sqrt{3}}{2} i \)
\( x= e^{i \cdot \frac{4 \pi}{3}} = cos \dfrac{4 \pi}{3} + i \cdot sin \dfrac{4 \pi}{3} = – \dfrac{1}{2} – \dfrac{\sqrt{3}}{2} i \)
\( x= e^{i \cdot 2 \pi} = cos 2 \pi + i \cdot sin 2 \pi = 1 \)

の三つ

n=4の場合（ \( x^4=1 \) の解）

方程式は\( x^{4}=1 \)

図からみれば、複素平面の実数軸上の”１”を基準にした正方形の各点が解

n=4を踏まえれば、\( e^{iφ} \) の円を4等分した点。上と同様に、

\( φ =\dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, 2\pi \) の円上の点が方程式の解。

オイラーの公式を使えば解は、

\( x= e^{i \cdot \frac{\pi}{2}} = cos \dfrac{\pi}{2} + i \cdot sin \dfrac{\pi}{2} = i \)
\( x= e^{i \cdot \pi} = cos \pi + i \cdot sin \pi = – 1 \)
\( x= e^{i \cdot \frac{3\pi}{2}} = cos \dfrac{3\pi}{2} + i \cdot sin \dfrac{3\pi}{2} = – i \)
\( x= e^{i \cdot 2 \pi} = cos 2 \pi + i \cdot sin 2 \pi = 1 \)

の四つ

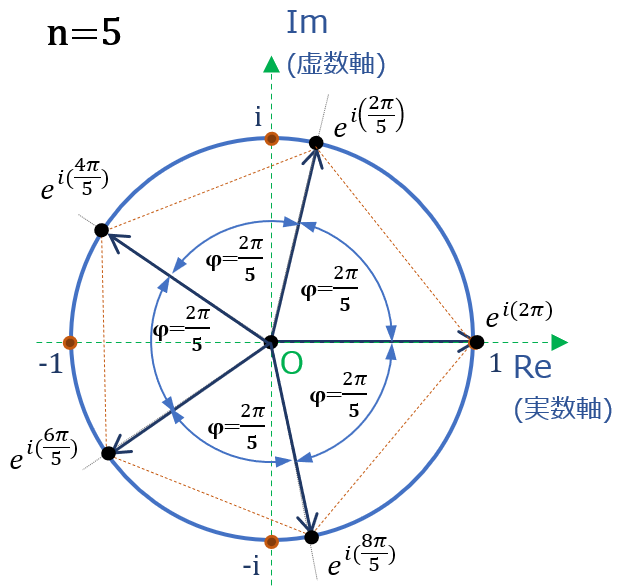
n=5の場合（ \( x^5=1 \) の解）

方程式は \( x^{5}=1 \)

図からみれば、複素平面の実数軸上の”１”を基準にした正五画形の各点が解

n=5を踏まえれば \( e^{iφ} \) の円を5等分した点、つまり

\( φ =\dfrac{2\pi}{5}, \dfrac{4\pi}{5}, \dfrac{6\pi}{5}, \dfrac{8\pi}{5}2\pi \)

の円上の点が方程式の解。

オイラーの公式を使えば解は、

\( x= e^{i \cdot \frac{2\pi}{5}} = cos \dfrac{2\pi}{5} + i \cdot sin \dfrac{2\pi}{5} \)
\( x= e^{i \cdot \frac{4\pi}{5}} = cos \dfrac{4\pi}{5} + i \cdot sin \dfrac{4\pi}{5} \)
\( x= e^{i \cdot \frac{6\pi}{5}} = cos \dfrac{6\pi}{5} + i \cdot sin \dfrac{6\pi}{5} \)
\( x= e^{i \cdot \frac{8\pi}{5}} = cos \dfrac{8\pi}{5} + i \cdot sin \dfrac{8\pi}{5} \)
\( x= e^{i \cdot 2 \pi} = cos 2 \pi + i \cdot sin 2 \pi = 1 \)

の五つ。簡単に算出できる。