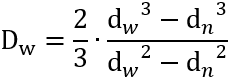ねじの強度区分、入力トルクと軸力(張力)の関係について

はじめに
ねじの強度区分
トルクと軸力（張力）の関係
軸力と摩擦力
トルク係数
1. 補足
2. まとめ
  1. 軸力計算ツール
入力トルク-軸力関係の特徴
追記

はじめに

前回の記事はねじの概要（ねじの名称、締結の仕組み、締め付け線図）までの概要。

ねじ 1)-1. ねじの名称、締結の仕組み、締め付け線図について

(ボルト)ねじの力学: ０スタートで設計の実務レベルの入り口（基礎）までを一気に。まずはねじの名称から。。

今回は、ねじの強度区分から入力トルクと軸力の関係まで

今回もこの二冊がベース

”ねじ締結の原理と設計”と”ねじ締結概論”。

posted with カエレバ

posted with カエレバ

ねじの強度区分

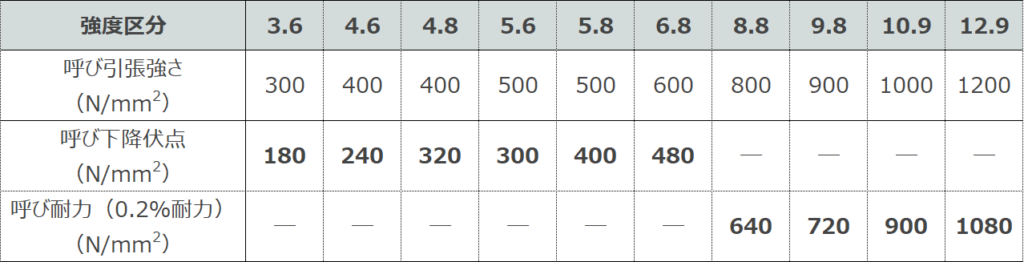
ボルトの強度区分は X.Y （例 8.8、10.9・・・）の数字で表記される。
小数点以上/以下で別の意味をもち、

小数点以上の数字 X：ボルトの呼び引張強さの1/100の値
小数点以下の数字 Y：X に対する呼び下降伏点 or 呼び耐力の割合の1/10の値

つまり、強度区分6.8の意味は、

ボルト/ナットの呼び引張強さが 600N/mm²
呼び下降伏点(か呼び耐力)の割合が80％で 480N/mm²（=600ｘ0.8）

となる。

この場合、設計で使う規格降伏点は 640N/mm² 。

（”呼び”とあるのは材料の機械的性質の値ではなく、ボルトの強度区分を示すための規格値のため。）

トルクと軸力（張力）の関係

前回の記事にも書いたが、入力されたトルクT_f（T）はボルト周りでみれば

ボルト座面に作用するトルク(b)：T_w
ねじ部に作用するトルク(a)：T_s

に分けられる。つまり、

T_f = T_w + T_s

座面に作用するトルク：T_w

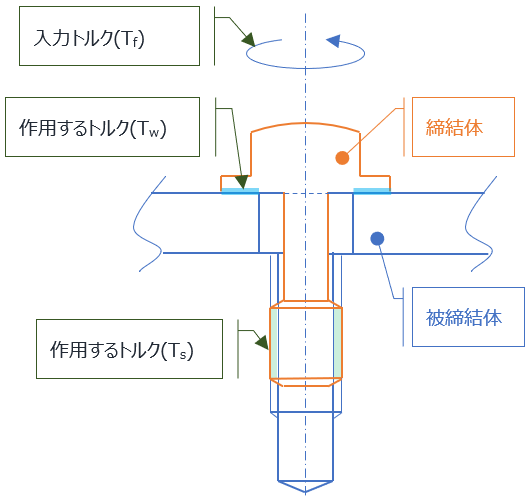
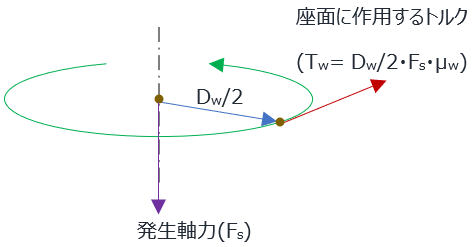
座面に作用するトルクT_wの算出

発生している軸力をF_s、座面の摩擦係数 μ_ｗ、座面等価摩擦直径をD_wとすれば、トルクT_ｗは

となる。また、ここでDwは、

Dw：座面等価摩擦直径

(d_w：座面径、d_n：ボルト穴径 )

を用いる。

言うまでもなく、これはただのモーメント計算（モーメント長ｘ力）と同じ。

ねじ面に作用するトルク：T_s

さて、ねじ面に作用するトルクT_s も、ただのモーメント計算。

少し違うのは、ねじ面は斜面となるので、斜面の定理を使って回転の行われる水平面（＝軸に直角面）の力を算出、これにモーメント長をかけてトルクTsを算出する必要がある。

ねじ面に作用するトルクT_s の算出

ねじ面に作用するトルクT_sは、ねじ面斜面に発生する力の水平成分をＵ、ねじの有効径をd_pとすると

である。

ここまでは、まだ水平面上のただのモーメント計算（Twと同じ）。

ここからUを算出するのに斜面の定理を入れ込むが、ちょっと複雑なのは、T_s が発生する斜面が一つの角度θではなく、ねじの山角 α、およびリード角βの合成した角度の斜面となっている事。
（バンク角のついた坂道みたいなもの）

この部分の説明（合成した角度における斜面の定理の導入）は、ちょっと量があるので後の記事にて。

ねじ 1)-6. 斜面の定理のねじ面への展開(詳細)

”ねじ面に作用するトルク Ts ” に必要な水平力Uの詳細説明。斜面の定理（ U＝ F tan( θ + ρ0) ）から展開する

今回はUの算出式まで一気にスキップ。

（斜面の定理の基礎的なトコロからであればこちらから）

基本的には斜面の定理を使いUを求める。

発生軸力をFs、ねじピッチP、ねじの有効径d_p 、ねじ面の摩擦係数 μ_s 、ねじの山の半角をαとし、斜面の定理を使えば、水平方向にかける力Uは、

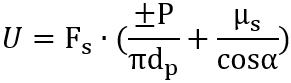
（+Pが締付け側、 -Pは緩め側）

これを使ってUにモーメント長の d_p/2 をかければ、ねじ面に作用するトルクT_sとなるため

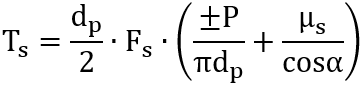
となる。

(入力トルク) = (座面に作用するトルク) + (ねじ面に作用するトルク)

以上の T_wとT_s を使えば、締付けトルク T_f_t は、T_f= T_w + T_s より

締付け側を T_fl 、ゆるめ側トルクを T_fl とすれば

・・・①

であり、

・・・②

である。

軸力（張力）の算出

式を変形すれば、F_sは

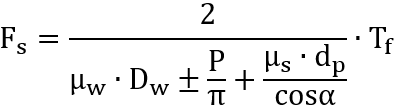
つまり、ねじの軸力は以下の仕様で決まる。

ねじの諸元
摩擦係数
入力トルク

軸力と摩擦力

入力したトルクが軸力に変換される割合を考える。

一旦整理すれば、

入力トルク(T_f)と軸力(F_s)の関係 (Motoshの式)

つまり、入力トルク (T_f) は、

座面の摩擦によるトルク
ねじ面の摩擦によるトルク
伸び（軸力発生）によるトルク

の3つに配分される

いくつかの例を簡単に計算してみる。

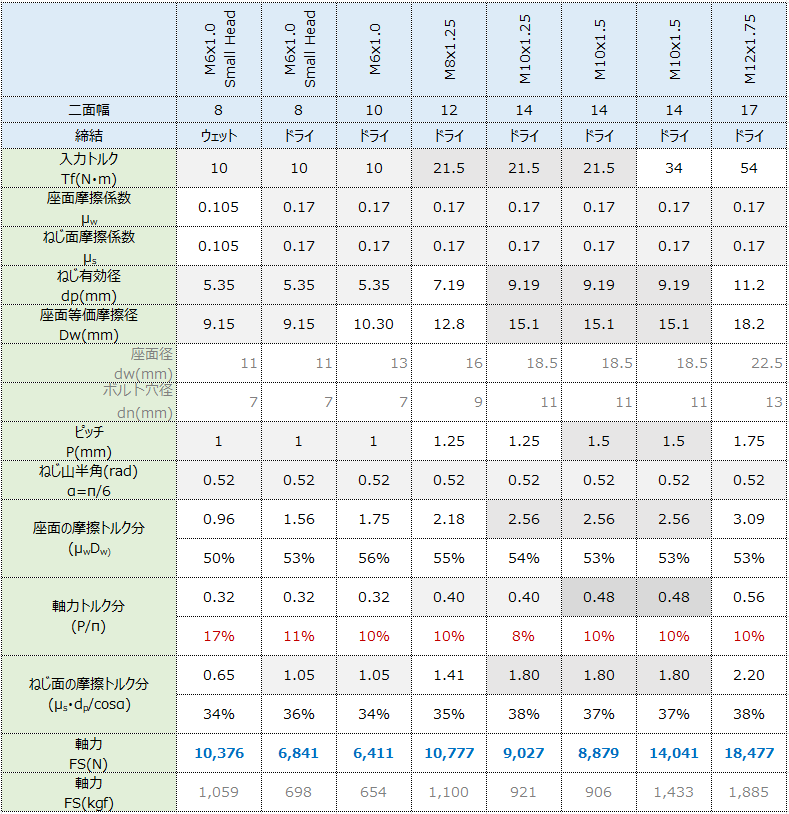
これをみれば、入力されるトルクは、

トルクの8-9割は、摩擦に消費される（座面（5～6割）、ねじ面（3～4割） ）。
軸力に変換される割合は最大でも2割もいかない（ドライ締付けでは1割程度）

である事がわかる（摩擦消費分を減らせば、軸力は上がる）。

この割合をイメージとして持っておく。

トルク係数

さて、式の簡易化するために、トルク係数がよく使われる。締め側のトルク

に、呼び径dを追加して、

ここから

とすれば①式は

T_f = (A_t・F_S)・d ・・・③

-> トルク (T_f )＝モーメント長(d) ｘ力 (A_t・F_S)

と見る事ができる。このA_t を、トルク係数と呼ぶ。

補足

さて、A_tもd もねじの諸元によってきまる定数、つまりA_t・dも定数。

T_f = (A_t・d)・F_S と再度書き直せば、トルク T_f と発生軸力F_S は、単純な線形一次の関係である事がわかる。

（トルクが10%Upすれば軸力も10％Up）

また、ついでに摩擦係数等の変化させる事よりトルク係数Atを変えた場合を考える（ A_t1,-> A_t2）。

T_f = (A_t1・d)・F_S1 = (A_t2・d)・F_S2 これから

F_S2 / F_S1 = A_t1 / A_t2

トルク係数の変化は発生軸力の変化と反比例する。

（トルク係数が10%Downすれば軸力は10％Upする）<- 例：摩擦係数を下げれば軸力は上がる

まとめ

トルク算出式とトルク係数

T_f = A_t・d・F_S

—–

ちなみに、 A_t はすべてねじの諸元できまる。

ねじの諸元：ねじピッチP、ねじ山の半角α、ねじ有効径d_p、座面等価摩擦直径D_w

摩擦係数：ねじ面摩擦係数 μ_s、座面摩擦係数 μ_ｗ

呼び径：d

軸力計算ツール

簡単に様々なボルトの軸力が計算できるように、軸力計算用のツールを作っておいた

入力トルク-軸力関係の特徴

さて以上を踏まえて、特徴をまとめると以下。

頭の片隅に置いておくとイロイロ便利

入力されるトルクは、ほとんどが座面とねじ面の摩擦に消費される（8-9割）。
摩擦を下げれば軸力はあがるが、軸力に変換されるトルクは最大でも2割もいかない。
（同一ボルトにおいて）
発生軸力の変化の割合は、入力トルクの変化の割合と等しい
- 例：トルクが10%Upすれば軸力も10％Up
（同一ボルト、同一トルクであれば）
発生軸力の変化の割合は、トルク係数の変化の割合に反比例する
- 例：トルク係数が10％Downすれば、軸力は10％Up（例：ウェット締付）
（同一ねじ径、同一締め付けトルクでは）
座面径を下げれば、軸力はあがる
- 例：頭部形状のみ異なるフランジボルトに同じトルクを入力した場合、座面径の小さいボルトの方が軸力は高い
（同一頭部形状、同一締付けトルクでは）
ねじ径が小さい方が軸力は高い
（同一ねじ径、同一頭部形状）
ねじピッチを下げれば、軸力は上がる

追記

つづいて、入力トルクの設定方法と管理（トルク法）について。

入力トルク管理にはトルク法、回転角法、トルク勾配法がある。

以下の記事にて

ねじ 1)-3. 締結トルクの設定について

ねじ（ボルト）の設定。トルク法での管理について詳細に。締結トルクの設定については、弾性域締付、塑性域締付があるが、組立て部品で交換可能を前提としているのであれば弾性域締付け。つまりトルク法。ボルトによりきまる設定トルクは、ボルトの使用、締結環境から算出可能。ついでに、えいやっと決める方法まで。