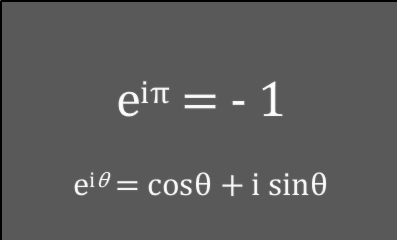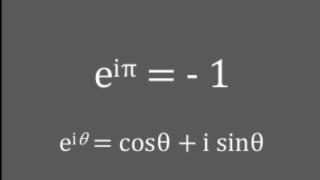オイラーの公式を導く
前回の記事は、オイラーの公式 :\( e^{i \theta}=cos \theta + i \cdot sin \theta \) ・・・① の見方と使い方の例について書いた。
今回は、この指数関数をつかった ” \( e^{i \theta} \) ” と 三角関数をつかった ” \( cos \theta + i \cdot sin \theta \) ” が等しい、というこの公式の導き方について。
先に結論を言えば、この公式は微分における各関数の性質とマクローリン展開(級数展開)を用いて、両辺が等しい事を導いている。
つまり、\( e^{i \theta} \)、\( cos \theta \) 、\( i \cdot sin \theta \) のマクローリン展開をみれば、
\( \begin{align}
e^{iθ} &= \dfrac{1}{0!}θ^{0} + \dfrac{i}{1!}θ^{1} + \dfrac{-1}{2!}θ^{2} + \dfrac{-i}{3!}θ^{3} + \dfrac{1}{4!}θ^{4} + \cdots ・・・②\\
cos θ &= \dfrac{1}{0!}θ^{0} +{\color{#d3d3d3}{ \cancel{\dfrac{0}{1!}θ^{1}}}} + \dfrac{-1}{2!}θ^{2} + {\color{#d3d3d3}{\cancel{\dfrac{0}{3!}θ^{3}}}}+ \dfrac{1}{4!}θ^{4} + \cdots ・・・③ \\
i \cdot sin θ &= {\color{#d3d3d3}{\cancel{\dfrac{0}{0!}θ^{0}}}} + \dfrac{i}{1!}θ^{1} + {\color{#d3d3d3}{\cancel{\dfrac{0}{2!}θ^{2}}}} + \dfrac{-i}{3!}θ^{3} +{\color{#d3d3d3}{ \cancel{\dfrac{0}{4!}θ^{4}}}} + \cdots ・・・④ \\
\end{align} \)
(斜線部は”0″)
明らかに ② = ③ + ④ が成り立つ。
したがって両辺が等しいと述べているに過ぎないが、この導入過程において、指数関数、三角関数、ネイピア数、虚数のそれぞれの性質、また、微分、級数展開といった手法が、巧みに利用されている。
これらの関数は本来まったく別々に(しかも異なる時代に)定義されたものであるにもかかわらず、そうとは思えないほど自然に結びついてくる。とにかく、見事。
その過程を一通り記載。
eの指数関数 \(e^θ \) 、三角関数 cosθ 、sinθ 、虚数 i の 各性質
ネイピア数の指数関数 \( e^θ \) 、三角関数 \( cosθ \) 、\( sinθ \)、虚数 \( i \) の各性質について、今回のオイラーの公式の導入に必要なトコロだけざっくりと
ネイピア数 e の指数関数 \( e^θ \) の微分の性質
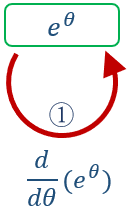
まず、ネイピア数 を使った指数関数 \( e^θ \) 。
これは微分において、何度微分しても \( e^θ \) のままという特別な性質を持っている。 (というか、そう定義された実数が \( e \))。つまり形を変えない。
\( \dfrac{d}{dθ}(e^θ) = e^θ \)・・・⑤
この性質についての覚書はこちら↓
三角関数 cosθ 、sinθ の微分の性質
続いて、三角関数。
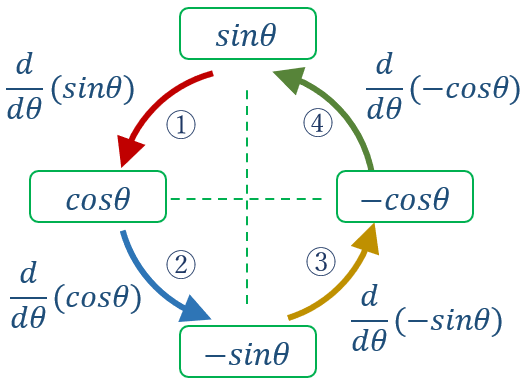
例えば、\( sinθ \)の微分を繰り返すと
\( sinθ \) -> \( cosθ \) -> \( – sinθ \) -> \( – cosθ \) -> \( sinθ \)
こちらは、微分を4回繰り返すと元に戻る。
虚数 i のかけ算
虚数単位 \( i \) は、\( i = \sqrt{-1} \) つまり
\( i ^2 = -1 \) ・・・⑥
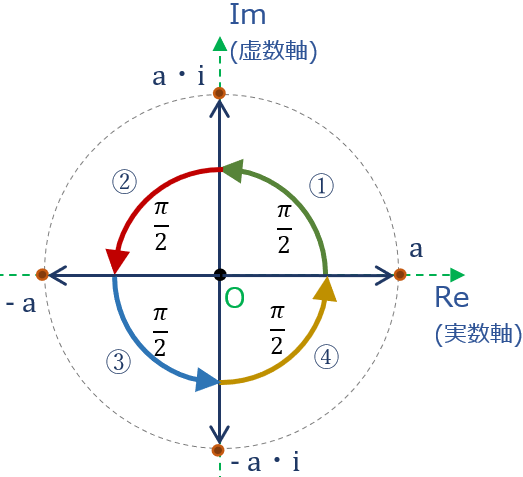
例えば、実数 \( a \) に繰り返し \( i \) をかけてみれば、
\( a \) -> \( a \cdot i \) -> \( -a \) (\( =a \cdot i ^2 \) ) -> \( -a \cdot i \) -> \( a \) (\( = -a \cdot i ^2 \) )
つまり、虚数 \( i \) を4回かけると元の実数に戻る。
くるくる回る虚数の振る舞いについては、こちらにも少し↓
マクローリン展開
級数展開の仕組みからマクローリン展開概要の覚書についてはこちら↓
抜粋すればテイラーの定理からテイラー展開(無限級数化)し、その中の微分の起点を”0”にとった限定版がマクローリン展開
↓この式が、そのマクローリン展開の式。
\( f(x) = \displaystyle \sum_{n=0}^{∞} \dfrac{f^{(n)}(0)}{n!}x^n \)
オイラーの公式を導くのには、級数展開であるこのマクローリン展開を使う。
注1:各関数 (指数関数 \(e^θ \)、三角関数 \(sinθ \)、\(cosθ \)) のテイラーの定理における剰余項 \(R_n \) が、\(n → ∞ \) の時 \(R_n → 0\) に収束する事からマクローリン展開が使用可能
注2:\(R_n → 0 \) は、ここでは既知として話を進める、証明はまた別途。
さて道具がそろったので、ここから本題のオイラーの公式
オイラーの公式の導き方
オイラーの公式は、\(e^θ \) 、 \(sinθ \)、\(cosθ \) をマクローリン展開した級数の組合せで簡単に算出できる。
\(e^θ \) 、sinθ 、cosθ のマクローリン展開
一旦 使用する関数を \(f(θ)\) として、マグローリン展開の級数項の微分の部分 \( f^{(n)}(0) \) を調べておく。
\(θ=0 \) であることと、上述の各性質をふまえれば、
- \( f(θ)=e^θ \) のとき、\( f^{(n)}(0) \) は ”1” のまま
- \( f(θ)=sinθ \) のとき、\( f^{(n)}(0) \) は \( 1 → 0 → -1 → 0 \) の循環
- \( f(θ)=cosθ \) のとき、\( f^{(n)}(0) \) は \(0 → 1 → 0 → -1 \) の循環
となっている事がわかる。
これに、虚数 \( i \) を組み合わせて表にすれば以下(下図)
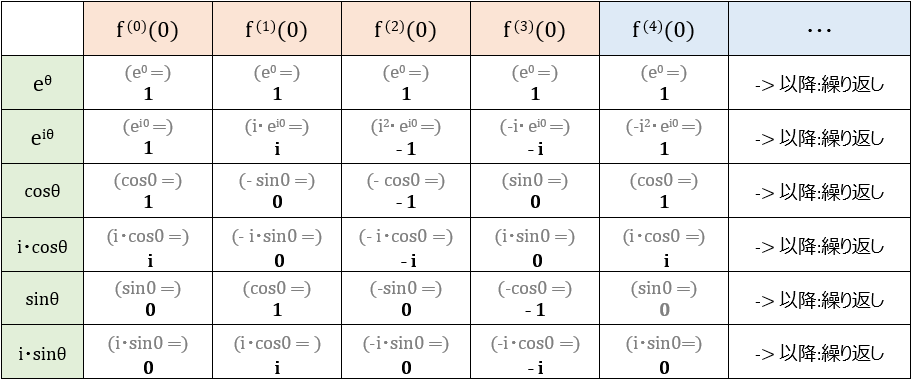
→ 虚数を組み合わせても、どの関数も マクローリン展開による級数展開時 \( f^{(n)}(0) \) の部分は、 ”微分を4回繰り返せば(同時に)元に戻る” というトコロが肝
上の表を参照に \(e^θ \) 、\(e^{iθ} \)、\(cosθ \)、\(i \cdot cosθ \)、\(sinθ \)、\(i \cdot sinθ \) を一通りマクローリン展開してみれば、
\( \begin{align}
{e^{θ}} &= \dfrac{1}{0!}θ^{0} + \dfrac{1}{1!}θ^{1} + \dfrac{1}{2!}θ^{2} + \dfrac{1}{3!}θ^{3} + \dfrac{1}{4!}θ^{4} + \cdots ・・・②’\\
e^{iθ} &= \dfrac{1}{0!}θ^{0} + \dfrac{i}{1!}θ^{1} + \dfrac{-1}{2!}θ^{2} + \dfrac{-i}{3!}θ^{3} + \dfrac{1}{4!}θ^{4} + \cdots ・・・②\\
cos θ &= \dfrac{1}{0!}θ^{0} +{\color{#d3d3d3}{ \cancel{\dfrac{0}{1!}θ^{1}}}} + \dfrac{-1}{2!}θ^{2} + {\color{#d3d3d3}{\cancel{\dfrac{0}{3!}θ^{3}}}}+ \dfrac{1}{4!}θ^{4} + \cdots ・・・③ \\
i \cdot cos θ &= \dfrac{i}{0!}θ^{0} + {\color{#d3d3d3}{\cancel{\dfrac{0}{1!}θ^{1}}}} + \dfrac{-i}{2!}θ^{2} + {\color{#d3d3d3}{\cancel{\dfrac{0}{3!}θ^{3}}}} + \dfrac{i}{4!}θ^{4} + \cdots ・・・③’ \\
sin θ &={\color{#d3d3d3}{ \cancel{\dfrac{0}{0!}θ^{0}}}} + \dfrac{1}{1!}θ^{1} + {\color{#d3d3d3}{\cancel{\dfrac{0}{2!}θ^{2}}}} + \dfrac{-1}{3!}θ^{3} +{\color{#d3d3d3}{ \cancel{\dfrac{0}{4!}θ^{4}}}} + \cdots ・・・④’ \\
i \cdot sin θ &= {\color{#d3d3d3}{\cancel{\dfrac{0}{0!}θ^{0}}}} + \dfrac{i}{1!}θ^{1} + {\color{#d3d3d3}{\cancel{\dfrac{0}{2!}θ^{2}}}} + \dfrac{-i}{3!}θ^{3} +{\color{#d3d3d3}{ \cancel{\dfrac{0}{4!}θ^{4}}}} + \cdots ・・・④ \\
\end{align} \)
(斜線部は”0” )
覚書:\(e^{θ} \)、cos θ、sin θ のマクローリン展開(Note: 0! =1)
\( \begin{align}
e^{θ} &= 1 + θ + \dfrac{1}{2!}θ^{2} + \dfrac{1}{3!}θ^{3} + \cdots + \dfrac{1}{n!}θ^{n} + \cdots \\
cos θ &= 1 + \dfrac{-1}{2!}θ^{2} + \dfrac{1}{4!}θ^{4} + \cdots + \dfrac{(-1)^n}{(2n)!}θ^{2n}+ \cdots\\
sin θ &= θ + \dfrac{-1}{3!}θ^{3} + \dfrac{1}{5!}θ^{5} + \cdots + \dfrac{(-1)^n}{(2n+1)!}θ^{2n+1} + \cdots \\
\end{align} \)
オイラーの公式
さて、ここまで来たらオイラーの公式までたどり着くのは簡単。 ②③④式をならべれば、一目で ② = ③+④ が成り立っている事がわかる
\( \begin{align}
e^{iθ} &= \dfrac{1}{0!}θ^{0} + \dfrac{i}{1!}θ^{1} + \dfrac{-1}{2!}θ^{2} + \dfrac{-i}{3!}θ^{3} + \dfrac{1}{4!}θ^{4} + \cdots ・・・②\\
cos θ &= \dfrac{1}{0!}θ^{0} +{\color{#d3d3d3}{ \cancel{\dfrac{0}{1!}θ^{1}}}} + \dfrac{-1}{2!}θ^{2} + {\color{#d3d3d3}{\cancel{\dfrac{0}{3!}θ^{3}}}}+ \dfrac{1}{4!}θ^{4} + \cdots ・・・③ \\
i \cdot sin θ &= {\color{#d3d3d3}{\cancel{\dfrac{0}{0!}θ^{0}}}} + \dfrac{i}{1!}θ^{1} + {\color{#d3d3d3}{\cancel{\dfrac{0}{2!}θ^{2}}}} + \dfrac{-i}{3!}θ^{3} +{\color{#d3d3d3}{ \cancel{\dfrac{0}{4!}θ^{4}}}} + \cdots ・・・④ \\
\end{align} \)
(パズルがすっきりと組み合わさる)
よって、
\( e^{i \theta}=cos \theta + i \cdot sin \theta \) ・・・①
にて、オイラーの公式が導かれる。
ここに \( \theta = \pi \) を代入すれば、” \( \pi \)” と ” – “(マイナス) の世界も加わって、
\( e^{i \pi}=-1 \) ← 世界で最も美しい式
追記
前回の記事にて \( e^{i \pi}=-1 \) が
と書いたが、導入に級数展開をも使い、過去の蓄積された数学の各世界のそれぞれのルールを崩すことなく統一しているのが、オイラーの公式。
ここが”美しい”と言われる所以。
上のテイラー展開については、こちらの本がおススメ(実数・虚数についてのおススメ本と同じ)
オイラーの公式については、この本もおすすめ。。
流し読みとまではいかないが、読み物としても面白い。