はじめに
虚数単位 \(i \) とは
\( i = \sqrt{-1} \)
つまり、\( i^2= -1 \)
ただ、2乗してマイナスになる数は実数では定義されていない。
この不思議な感覚と実の数に対する”虚”の数という”名前から、なにやら理解不能なイメージがつきまとう。少し数字の世界(概念)を広げる必要がある。
元数と虚数
実数の連続した直線に、同じ連続した直線の概念にて別軸を加え、数の概念を直線から平面に少し広げる。
つまり、2乗しても実数をマイナスにする事を可能になる概念。
このために新たに加える軸が”虚数”軸(単位: i)、この軸上の数が虚数
この虚数軸は実数軸に直行、つまり互いに独立した直行軸 ( = 互いに干渉しない )。
ちなみに、実数と虚数というと、この世とあの世(見える世界と見えない世界)みたいなイメージがあるが、ともに実在する数。
(同レベルで互いに独立。ただ片方の世界からはもう片方の世界に干渉しないだけ、と、とらえる)
さて、この”それぞれに独立した数の世界の数” を表すのに元数という言葉を使う。
この場合は、二元数という。
また、この二元数は複素数と呼ばれ、 \( Z \) とすると
実数部を\(a\)、虚数部を \(b\cdot i \) とすれば
\( Z = a +b \cdot i \)
( \(a,b \) は実数)
\( Z \) を構成する実数軸と虚数軸がなす平面が、複素平面(ガウス平面)と呼ばれる。
(ちなみに、実数軸二軸で構成するゆがみのない二次元平面はユークリッド平面 <- ただの覚書 )
二元数以外にも、実数軸x1、虚数軸x3の計4つの世界からなる数は、四元数(クォータニオン)と呼ばれ、空間上の回転を計算する時とかに使われる。
複素数 Z の性質
この \( i \) を使った \( Z \) は以下の性質を持つ。
\( Z_0 = a_0 +b_0 \cdot i \) とし、繰り返し \( i \) をかけていくと
\( \begin{array}{cccc}
&Z_0 &=& a_0 &+& b_0 \cdot i \\[6pt]
→ ( \times i ) → &Z_1 &=& a_0 \cdot i &-& b_0 \\[6pt]
→ ( \times i ) → &Z_2 &=&- a_0 &-& b_0 \cdot i \\[6pt]
→ ( \times i ) → &Z_3 &=& – a_0 \cdot i &+& b_0 \\[6pt]
→ ( \times i ) → &Z_4 &=& a_0 &+&b_0\cdot i \\[6pt] &&=& Z_0 \end{array} \)
\( i \) を4回かければ、複素数 \( Z \) は元に戻る。
この動きを複素平面で見る。
Zn (n=0,1,2,3,4) を複素平面上の座標でとると
\( \begin{array}{cccc}
Z_0 : &(a_0 &,& b_0\cdot i ) \\[6pt]
Z_1 : &(-b_0 &,& a_0 \cdot i) \\[6pt]
Z_2 : &(-a_0& , &-b_0\cdot i)\\[6pt]
Z_3 : &(b_0 &,& -a_0\cdot i) \\[6pt]
Z_4 : &(a_0&,& b_0\cdot i)
\end{array} \)
になる(図①参照)。
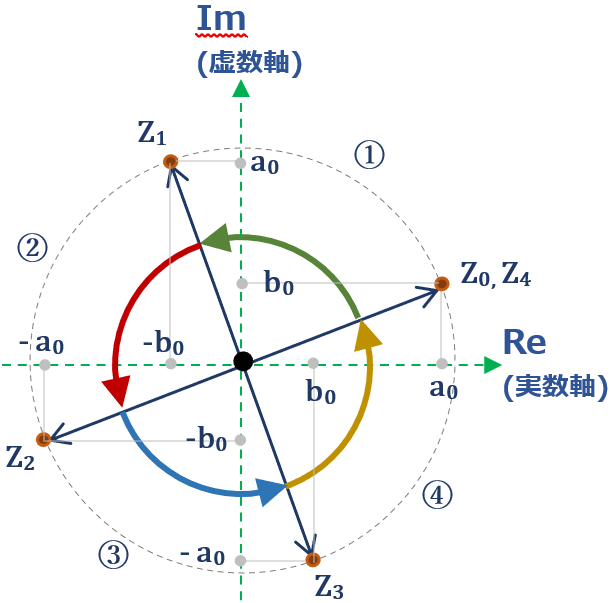
この Zn をベクトルとしてみれば、
i をかけるごとに、Zn は π/2 づつ回転する
このベクトル Zn は複素ベクトルと呼ばれる。
実数軸で正負の逆転をさせる事は、このベクトルを逆方向に向けさせればよい(=180°回転させてやればよい)。これは、複素数に \( i \) を二回かける事と同義 (= \( i^2 \))
<- これが二乗すると負となるからくり ( i2 = -1 のしくみ (というか定義))
また、虚数軸は実数軸と同じ元数。同じレベル。つまり、虚数軸側についても全く同じ使い方ができる。
ついでに、この二元数 Z の表記( Z= a + b i )は、実数軸の二次元平面の任意ベクトルと見る時の感覚と似ている。つまり 、i 、 j をxy軸の正規直行基底とした時の、c = a i + b j 。(a b)が xy軸の座標値となるとの同じ。
違いは、i をかけるごとにぐるぐる回る事。
