はじめに
ベクトルの内積については前回の記事を参照
今回はベクトル外積。外積も使い道が明確にある。外積の定義と計算方法/計算則から。
ベクトルの外積 (cross-product)
外積の定義と意味
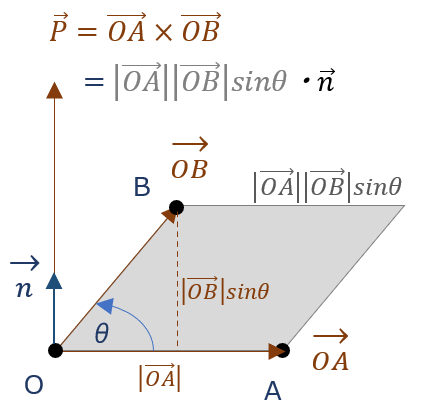
内積とは違い、外積はベクトル ( \( \small {\overrightarrow{P}} \)とする)
\( \small {\overrightarrow{OA}} \)、\( \small {\overrightarrow{OB}} \) のなす角 \(θ \)、\( \small {\overrightarrow{OA}} \)、\( \small {\overrightarrow{OB}} \) それぞれに直角な単位ベクトル \( \small {\overrightarrow{n}} \) とし、\( \small {\overrightarrow{n}} \) の方向は、\( \small {\overrightarrow{OA}} \) から \( \small {\overrightarrow{OB}} \) に回転させた時に右ねじが進む方向と一致させる。
この時に、\( \small {\overrightarrow{OA}} \)、\( \small {\overrightarrow{OB}} \) の外積 \( \small {\overrightarrow{P}} \) は
\( \begin{align}
\overrightarrow{P} &= \overrightarrow{OA} \times \overrightarrow{OB} \\[6pt]
&= | \overrightarrow{OA}| \cdot |\overrightarrow{OB}| \cdot sinθ \cdot \overrightarrow{n} ・・・⑦
\end{align} \)
にて定義される。\( \small {\overrightarrow{P}} \) の大きさ ( \( \small {|\overrightarrow{P}|} \) ) は、\( \small {\overrightarrow{OA}} \) と \( \small {\overrightarrow{OB}} \) で形成される平行四辺形の面積）
つまり外積は、”掛け合わせる二つのベクトルに共に直行する向き” をもち、かつ ”掛け合わせる二つのベクトルがなす平行四辺形の面積を大きさ” にもつベクトルを示す。
外積の計算則
外積の分配法則も成り立つ
\(\vec{a} \times ( \vec{b} + \vec{c} ) \) = \( \vec{a} \times \vec{b} + \vec{a} \times \vec{c}\)・・・⑧
\( (\vec{b} + \vec{c}) \times \vec{a} \) = \( \vec{b} \times \vec{a} + \vec{c} \times \vec{a}\)・・・⑨
定数倍も成立
\( (t\vec{a}) \times \vec{b} = \vec{a} \times (t\vec{b}) = t\vec{a} \times \vec{b} \)・・・⑩
順序が変われば、外積ベクトルの向きが変わる(正負が入れ替わる)
\( \vec{a} \times \vec{b} = – \ \vec{b} \times \vec{a} \)・・・⑪
外積の成分計算
再度、内積の時と同様に、Oを原点にもつO-XYZ座標系（直行座標）を設定し、各x、y、z軸の単位ベクトルを \( \vec{i} \) = \( \left ( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right ) \) 、\( \vec{j}\) = \(\left ( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right )\)、\( \vec{k}\) = \(\left ( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right )\) とする。
各単位ベクトルは互いに直行しているので、外積の定義からこれらは以下の性質を持つ。
\(\vec{i} \times \vec{j}= -(\vec{j} \times \vec{i})=\vec{k}\)・・・⑫
\(\vec{j} \times \vec{k}= -(\vec{k} \times \vec{j})=\vec{i}\)・・・⑬
\(\vec{k} \times \vec{i}= -(\vec{i} \times \vec{k})=\vec{j}\)・・・⑭
\(\vec{i} \times \vec{i}= \vec{j} \times \vec{j}= \vec{k} \times \vec{k}=0\)・・・⑮
さて、O-XYZ上に点A : \( ( x_a \ , \ y_a \ , \ z_a ) \)、点B : \( ( x_b \ , \ y_b \ , \ z_b ) \) を設定し各軸の単位ベクトルを使えば、\( \small{\overrightarrow{OA}} \) , \( \small{\overrightarrow{OB}}\) はそれぞれ、
\( \overrightarrow{OA}=x_a\vec{i}+y_a\vec{j}+z_a\vec{k}\)
\( \overrightarrow{OB}=x_b\vec{i}+y_b\vec{j}+z_b\vec{k}\)
これに⑫～⑮式（と前述の計算則）を踏まえ、外積の成分計算を行う。
\( \begin{align} \overrightarrow{P}&=\overrightarrow{OA}\times\overrightarrow{OB}\\[8pt]
&= (x_a\vec{i}+y_a\vec{j}+z_a\vec{k})\times (x_b\vec{i}+y_b\vec{j}+z_b\vec{k})\\[8pt]
&= (y_a z_b – z_a y_b)\cdot(\vec{j}\times\vec{k})+(z_a x_b-x_a z_b)\cdot(\vec{k}\times \vec{i})+(x_a y_b-y_a x_b )\cdot(\vec{i}\times \vec{j}) \\[8pt]
&= (y_a z_b-z_a y_b)\cdot\vec{i}+(z_a x_b-x_a z_b)\cdot\vec{j}+(x_a y_b-y_a x_b )\cdot\vec{k} \\[6pt]
&= (y_a z_b-z_a y_b)\left (\begin{array}{c}1\\ 0\\ 0 \end{array} \right)+(z_a x_b-x_a z_b) \left ( \begin{array}{c}0\\ 1\\ 0 \end{array}\right)+(x_a y_b-y_a x_b ) \left ( \begin{array}{c}0\\ 0\\ 1 \end{array}\right) \\[6pt]
&= \left ( \begin{array}{c}y_a z_b-z_a y_b \\
z_a x_b-x_a z_b \\
x_a y_b-y_a x_b \end{array}\right)・・・⑯ \end{align}\)
行列式からの成分計算
さて、成分計算の理屈は上述の通りであるが、計算自体は行列式から解いてもOK。こっちの方が規則的に解けるので覚えやすい(いわゆるたすき掛け計算)
\( \begin{align} \overrightarrow{OA}\times\overrightarrow{OB} &= \left | \begin{array}{ccc}\vec{i}&\vec{j}&\vec{k}\\ \hline x_a&y_a&z_a\\x_b&y_b&z_b \end{array} \right|=\left | \begin{array}{cc} y_a&z_a\\y_b&z_b \end{array} \right|\vec{i}+\left | \begin{array}{cc} z_a&x_a\\z_b&x_b \end{array} \right|\vec{j}+\left | \begin{array}{cc} x_a&y_a\\x_b&y_b \end{array} \right| \vec{k} \\[8pt]
&= (y_a z_b-z_a y_b)\vec{i}+(z_a x_b-x_a z_b)\vec{j}+(x_a y_b-y_a x_b )\vec{k} \\[8pt] &= \left ( \begin{array}{c}y_a z_b-z_a y_b \\
z_a x_b-x_a z_b \\
x_a y_b-y_a x_b \end{array}\right)・・・⑯’ \end{align} \)
外積ベクトルの大きさ
また、成分を使えばこの外積ベクトル \( \small{\overrightarrow{P}} \) ( \(\small{= \overrightarrow{OA}\times\overrightarrow{OB}} \) ) の大きさは
\(\begin{align} |\overrightarrow{P}|&=|\overrightarrow{OA}\times\overrightarrow{OB} | \\[8pt] &= \sqrt { (y_a z_b-z_a y_b)^2+(z_a x_b-x_a z_b)^2+(x_a y_b-y_a x_b )^2}\end{align}\)
にて成分から外積ベクトルの大きさが算出できる。
二つのベクトルの間の角は⑦式の \( \small{\overrightarrow{P}}＝\small{|\overrightarrow{OA}|} \cdot \small{|\overrightarrow{OB}|} \ sin\theta \cdot \vec{n} \) を用いれば、\(\small{|\overrightarrow{P}|}=\small{|\overrightarrow{OA}\times\overrightarrow{OB}) |=|\overrightarrow{OA}|\cdot |\overrightarrow{OB}|} \cdot sin\theta\) より
\( sin\theta =\displaystyle\frac {|\overrightarrow{OA}\times\overrightarrow{OB} |}{|\overrightarrow{OA}|\cdot|\overrightarrow{OB}|}=\displaystyle\frac{\sqrt { (y_a z_b-z_a y_b)^2+(z_a x_b-x_a z_b)^2+(x_a y_b-y_a x_b )^2}}{\sqrt { {x_a}^2+{y_a}^2+ {z_a}^2}\cdot\sqrt { {x_b}^2+{y_b}^2+ {z_b}^2}} \)
から求まる。
さて何に使うの？・・・であるが、この外積表示は、回転体の速度 \(\vec{v} \) 表示において、頻繁に目にする。
このために定義されているのではないの？と思うぐらいぴったりの定義。ざっくりとは。。。
回転体の角速度を \(\vec{\omega} \)、回転体の中心軸上の原点 O から 回転体上の点Rへのベクトルを \( \vec{r} \) にとると
\(\vec{v} \) = \(\vec{\omega} \times \vec{r} \)
にて、回転に伴って向きが変わる点Rの速度 \(\vec{v} \) の一発表示が可能。
これは、外積の定義が、\(\vec{v} \) の長さである \( | \vec{\omega} | \) と \( | \vec{r} | \) (\( \vec{r} \) の回転中心軸から点Rまでの距離）の掛け算と、その向き（ \(\vec{\omega} \) と \( \vec{r} \) の互いに直角方向のベクトル）を同時に含む事が、点Rの速度 \(\vec{v} \) の表示を可能にしている。
追記
外積は”質点/剛体の動き”を考える上で角速度の表現で頻繁に目にする（<-こちらは別記事にて）。
（回転体を計算しようとする時には、外積は使えるようにしておいた方が何かと便利。。というか必須かも。）
さて次の記事では、一旦ベクトルの内積に戻って、内積の特長とベクトルの正規性の特長を使ったベクトルの投影長の算出を詳細に。というのも、こちらが座標軸の軸変換（座標値算出）の理解につながる。
->ざっくりとは、行列の積の成分計算がベクトルの内積と同じである事を利用して（行ベクトルと列ベクトルの内積）、その行列計算の意味が正規行列であれば座標軸変換である事の説明を。
その先、続けて回転行列、オイラー角までつないでいってみようかと。。
まずはベクトルの正規直行性から。次の記事にて。
