はじめに
締結トルクの設定方法(トルク法)が前回の記事
さてさて、トルク入力時の締結体の破損としては、
- めねじのねじ山が抜ける:めねじ部破損
- おねじのねじ山が抜ける:おねじ部破損
- おねじの軸が破断する:軸部破断/破損
である(被締結体側の破損(座屈/割れ等)についてはここでは除外)。
設計時には、規定トルク入力に対して上記状況のいずれも発生しない配慮が必要になる。
また、規定トルク以上の入力(いわゆる過大トルク入力)によるねじ抜けについては作業不良としてよい。
つまり、過大トルク入力時の破損形態についての設計計算は必須ではない。
とはいうものの、、、、
もし、過大トルク入力時にねじ抜けが発生した場合は、設計的には締結体として交換コストの一番安い部品、もしくは交換が容易である部品が壊れる方が良いとされる。
->作業復帰が容易なため。(例えばめねじ側が数万円の部品だった場合、ねじ山が破損するのは数円のボルトを交換する方がダメージが少ない。。。)
さてさて、
今回の記事はこれらの破損防止(いわゆる”ねじ抜け”)を目的に、
- 規定トルクに対して、ねじのかかり代(勘合長)をどう設定するか?
(ついでに、過大トルクが入力されたときにどこが最初に壊れるか?)
の話。
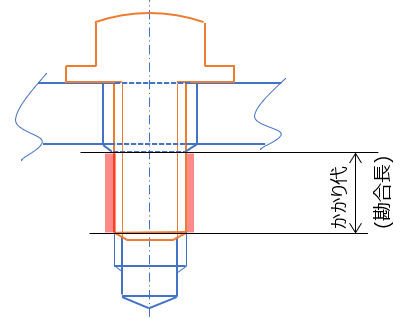
今回も”ねじ締結概論”が参考書 (ねじ締結概論 増補/養賢堂/酒井智次)
計算に入る前に。。
ちなみに、全締結部に対して勘合長をすべて計算している人などほぼいない(はず)。
(時間がなんぼあっても足らなくなる)。
ほとんどの場合は、母材強度踏まえた上での”経験値/実績値”ベースの勘合長設定。
”経験値/実績値”ベースの例としてよく聞くのが、ねじの呼び径dとした時、勘合長Lは
- めねじ材が鋼/アルミ展伸材の場合:L=1d ~ 1.5d (ねじ径の1~1.5倍)
- めねじ材がアルミ鋳物の場合:L=2d (ねじ径の2倍)
で設定しておけば、だいたい大丈夫とか。
(締付けの設定トルクまともであれば、ねじ山破損が発生する事はまずない)。
ちなみに、上の参考書には、VDI2230 Blatt2(1986)表12が付録にあり、それによれば。。
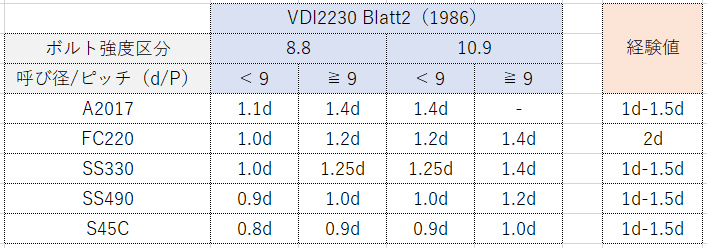
とある。これからすると、経験値ベースの設定は少し余裕度があり(勘合長が長めの安全側の設定になる)。
さてさて、
真面目な計算に追い込まれるのは、設計的な制限があり勘合長を詰めなければならない時。以下はその場合に備えて、の話。。やる/やらないは別として、計算できて損はない。
ねじ部(ねじ山)の破損
ねじ山の破損は、(当たり前ではあるが)”ねじ山に作用する力(Fex)” が、”ねじ山の強さ(Fm)” を超えた時に発生する。
つまり、Fex > Fm で破損。
まずは、”ねじ山の強さ(Fm)” の求めてみる。
ねじ山の強さ
”ねじ山の強さ(Fm)”は、 ”ねじ山のせん断される面積 (A)” に ”材料のせん断強さ(\( \tau_B\))”をかければよい。
つまり、
\( F_m = A \times \tau_B \)
ねじ山のせん断面積(おねじ&めねじ)
さて、”勘合部のねじ山の底辺の長さ(三角形の底辺)”をまず求める。
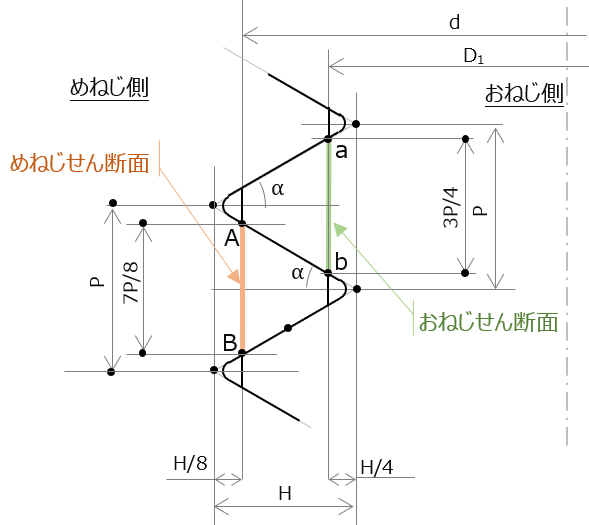
(参考書では一般化してあり小難しので、ここでは並目/細目のねじの諸元 の 呼び径d と めねじの山径D1 をそのまま使う(上図)。(計算も簡単になる。。))
めねじ山(三角形の)底辺の長さABは、
\( \tt \overline{AB}=\displaystyle \frac{H-\frac{1}{8}H}{H}P=\displaystyle \frac{7}{8}P \)
おねじ山(三角形の)底辺の長さabも同様に、
\( \tt \overline{ab}=\displaystyle \frac{H-\frac{1}{4}H}{H}P=\displaystyle \frac{3}{4}P \)
続いてその次、”おねじとめねじが勘合している長さ” を求める。
ねじの1ピッチあたりの周長(らせん状)は、めねじ側\( \tt \sqrt{(\pi d)^2+P^2 } \)、おねじ側 \( \tt \sqrt{(\pi D_1)^2+P^2 } \)となるが、ここでは参考書に従い(簡易化と安全側に振るとして、)リード角0、つまりP=0を使い、
- めねじ側1周長:\( \tt \pi d \)
- おねじ側1周長: \(\tt \pi D_1\)
で簡易化。勘合山数は、勘合長をLmとすれば \( \tt \displaystyle \frac{L_m}{P} \) 山である事から合わせて、
ねじ山の全周長(めねじ側LmN、おねじ側LmB)はそれぞれ
- \( \tt L_{mN}=\pi d \cdot \displaystyle \frac{L_m}{P} \\[12pt] \)
- \( \tt L_{mB}=\pi D_1\cdot \displaystyle \frac{L_m}{P} \)
となる。
各ねじ山のせん断面積(めねじ側 AAB、おねじ側 Aab)は、この全周長に先のねじ山底辺の長さ(\( \tt \overline{AB}、\tt \overline{ab})\)かけてやればよいので、
\(
\begin{align}
\tt A_{AB}&=\tt \overline{AB}\cdot \tt L_{mN}=\displaystyle \frac{7}{8}P\cdot \pi d \cdot \displaystyle \frac{L_m}{P} \\[8pt]
&=\tt \displaystyle \frac{7\pi}{8}\cdot L_m \cdot d
\end{align}
\)
\(
\begin{align}
\tt A_{ab}&=\tt \overline{ab}\cdot \tt L_{mB}=\displaystyle \frac{3}{4}P\cdot \pi D_1 \cdot \displaystyle \frac{L_m}{P} \\[8pt]
&=\tt \displaystyle \frac{3\pi}{4} \cdot L_m \cdot D_1
\end{align}
\)
となる。
ねじ山の強さ
ねじ山の強さはこの面積\( \tt A_{AB}、\tt A_{ab}\)に、めねじ材/おねじ材のそれぞれのせん断強さをかけてやればよいだけ。
ナット側材料のせん断強さ:\( \tau_{BN}\)、ボルト側材料のせん断強さ:\( \tau_{BB}\) とすれば、
めねじ山の強さFmNは、
\(
\begin{align}
\tt F_{mN}&= \tt A_{AB} \cdot \tau_{BN} \\[8pt]
&=\tt \displaystyle \frac{7\pi}{8}\cdot L_m \cdot d \cdot \tau_{BN} ・・・①
\end{align}
\)
おねじ山の強さFmBは、
\(
\begin{align}
\tt F_{mB} &= \tt A_{ab}\cdot \tau_{BB} \\[8pt]
&=\tt \displaystyle \frac{3\pi}{4} \cdot L_m \cdot D_1 \cdot \tau_{BB} ・・・②
\end{align}
\)
また、ついでにねじの諸元 から \(\tt D_1=\tt d-\displaystyle \frac{5P}{8\tan{\alpha}}\) を使えば②は
\( \tt F_{mB}=\displaystyle \frac{3\pi}{4} \cdot L_m\cdot \tau_{BB}\cdot (\tt d-\displaystyle \frac{5P}{8\tan{\alpha}}) \) ・・・③
となり、D1は消せる
-> ねじの一般諸元のみで表現できる
ねじ山強さと材料の引張強さ\( \sigma_{B}\)の関係
せん断ひずみエネルギー説のミーゼス応力 \( \sigma_{B}=\sqrt{\sigma^2+3\tau^2}\) に従ってねじ山が破損するとする。
せん断強さは \( \sigma = 0 \) から算出して , \( \sigma_{B}=\sqrt{3}\tau_{B} \) ( \( \tau = \tau_{B} \):せん断強さ)
これを変形して、
\(\tau_{B} =\displaystyle \frac{1}{\sqrt{3}}\sigma_{B} ≒ 0.577\sigma_{B}\)
この理論値に加え、(参考書によれば)材料のせん断強さ:\( \tau_{B}\)と材料の引張強さ\( \sigma_{B}\)は以下の関係も示されている(実験結果ベース)。
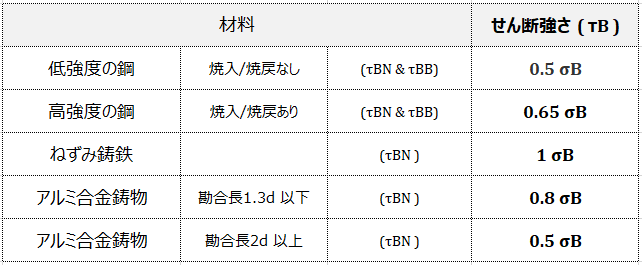
めねじ材の引張強さを\(\sigma_{BN}\)、\( \tau_{BN}=x \cdot \sigma_{BN}\)、おねじ材の引張強さを\( \sigma_{BB}\)、\( \tau_{BB}=y \cdot \sigma_{BB}\)として、①式と②式を書き直せば
①式:めねじ山の強さFmN
\( \tt F_{mN}=\tt \displaystyle \frac{7\pi}{8}\cdot L_m \cdot d \cdot \cal x \cdot \tt \sigma_{BN} \) ・・・④
②式:おねじ山の強さFmB
\( \tt F_{mB}=\tt \displaystyle \frac{3\pi}{4} \cdot L_m \cdot D_1 \cdot \cal y \cdot \tt \sigma_{BB} \) ・・・⑤
つまり、おねじ/めねじのねじ山の強さは
- \( \tau_{BN} 、\tau_{BB} \) の値がわかっていれば、その値を①②式へ代入して算出
- \( \tau_{BN} 、\tau_{BB} \) が不明であれば、材料の各引張強さと表②を使って\( \tau_{BN}=x \cdot \sigma_{BN}\)、\( \tau_{BB}=y \cdot \sigma_{BB}\)を求め、④⑤式から算出
- 全く手がかりがなければ、理論値のx、y=0.57、および材料の各引張強さを使って \( \tau_{BN}=0.57 \sigma_{BN}\) 、\( \tau_{BB}=0.57 \sigma_{BB}\)として算出
にて求める事ができる(設計的な見通し)。
補足
さて、表②の下の二段、同一材(アルミ合金鋳物)にもかかわらず、せん断強さ\( \tau_{B}\)が勘合長違いで異なっている。
(0.8\( \sigma_{B}\)と0.5\( \sigma_{B}\))
これは、勘合長が長い場合、ボルト先端側のねじ山より先に根元側(頭部側)のねじ山が破壊し始める故である(ねじ山の荷重分担が実際には頭部側のねじ山に偏るため)。
これに対し、①式&②式から導くねじ山の強さは、勘合する全てのねじ山に力が均質にかかる事が前提。
-> 表②の下二段のアルミ合金鋳物のせん断強さの差は、この事象に対する補正分であり材料が違うわけではない。
さて、つづいて本題の勘合長の設定について
勘合長の設定
さて、
設定トルクでねじ山が破損しないために、”Fex:ねじ山に作用する力”には、トルク設定計算時に算出される最大発生軸力FsHを当てはめる(トルク法での管理内)。
式でかけば、めねじ側 FmN > FsH 、おねじ側 FmB > FsH
この関係を使っておねじ/めねじで最小勘合長をそれぞれ算出、長い方を勘合長LmとすればOK。
->おねじの諸元から算出する最大トルク入力時に対し、勘合長Lmにてねじ抜けの発生なし
Note: 最大発生軸力FsHは、こちら参照 & FsHの計算値は、計算ツールの”補足情報2”内に計算結果あり
使用する式は、\( \tt F_{sH}=A_s\cdot\xi \cdot \sigma_{yB} \) ・・・⑥ である。
有効断面積 As、係数ξは記事のまま。σyBはおねじ材の耐力(降伏応力)
さて、計算。
めねじ側に必要な勘合長LmNは、めねじ側の条件 FmN > FsH より、 ④式&⑥式 を使えば
\( \tt L_{mN} >\displaystyle \frac{8\cdot \tt A_s\cdot\xi \cdot \sigma_{yB}}{7\pi\cdot d\cdot \cal x \cdot \tt \sigma_{BN}}\) ・・・⑦
同様におねじ側に必要な勘合長LmBは、FmB > FsH より ⑤式&⑥式 を使えば
\( \tt L_{mB} >\displaystyle \frac{4\cdot \tt A_s\cdot\xi \cdot \sigma_{yB}}{3\pi\cdot D_1\cdot \cal y \cdot \tt \sigma_{BB}}\) ・・・⑧
勘合長Lmは このLmN、LmBの長い方。
おねじの軸の破損
ここでは、おねじの軸自体が破損する時の荷重(FaB)は、おねじの材料の引張強さ(σBB)を使って
FaB=σBB・As (σBB:おねじの材料の引張強さ、As:軸の有効断面積)
としておく。
ボルトの破断 / おねじ部破損 / めねじ部破損
さて、冒頭にあげた”締結時に発生するねじの破損”の3か所
- めねじがねじ抜けする時の荷重(=めねじ山の強さ):FmN
- おねじがねじ抜けする時の荷重(=おねじ山の強さ):FmB
- ボルトの軸の破断荷重:FaB
に加え、ボルトの諸元から決まるFsH(設定可能な限界軸力)を比較すれば、
- トルク法での最大(限界)トルク入力時に、ねじ山が破損しないか
- 過大トルクが入力された場合に、どの箇所が破損するか
がわかる事になる。
簡単に言えば、限界軸力がおねじ&めねじのねじ山の強さを超えなければ、締結時にねじ抜けは発生しない。また、過大トルク入力時の破損する箇所は上記のNo.1~No.3の荷重値が最弱の箇所。
計算ツール
算出用にツールを作っておいた。
おねじの諸元からトルク法において入力できる最大トルク(限界トルク)を算出 + そのトルク時の最大発生軸力から、ねじ抜けの発生有無まで自動で計算するツール。
計算例
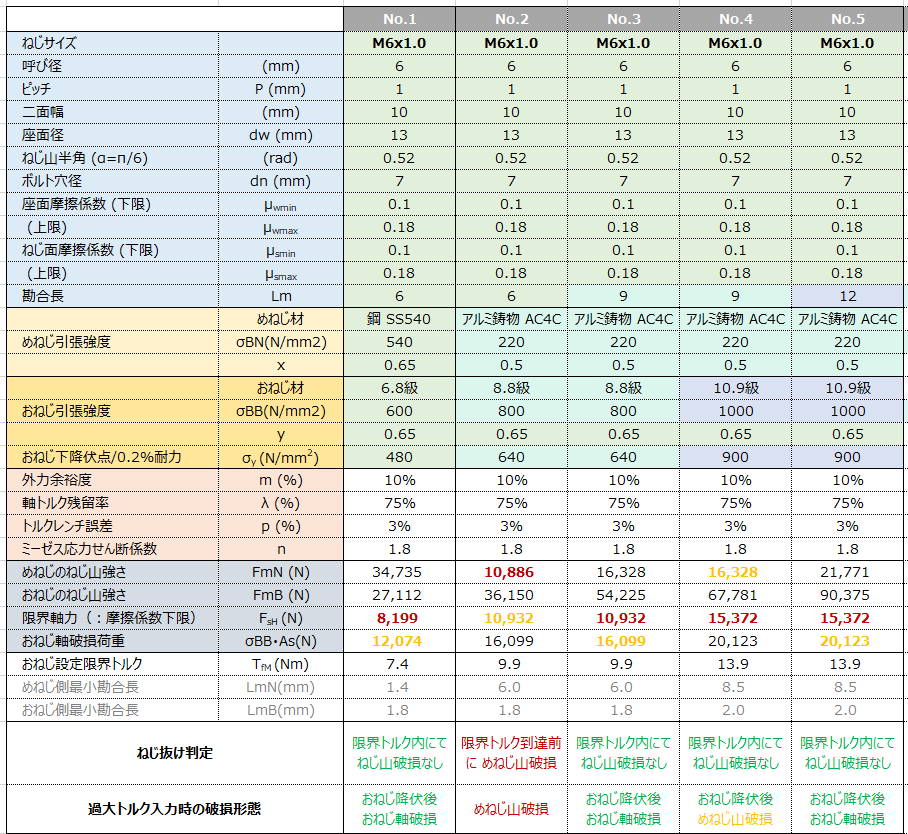
さて、一例として、M6ボルトを例にざざっと計算。
一番左(No.1)は、おねじ/めねじの材料強度はほぼ同じに設定、勘合長は Lm=dにて想定。
(特に意味はないが、そもそも各部位の強さってどんなレベル?の比較のため(感覚づけ)。。)
->結果:ねじ山強度は”おねじ<めねじ” だが、勘合長dのおかげでどちらのねじ山も十分に強く、過大トルクが入力されても、おねじの軸破断が最初に発生する。
No.2~6はめねじ側がアルミ鋳物、ねじ径6mmで統一。勘合長&おねじ材料強度を変化させた時の破損の変化具合。
表の一番下のコメントが、計算結果によるねじ抜け判定と過大トルク入力時の破損形態。
(表内の赤数字は最弱部、黄色が二番目)
この表(各ケース)についていえば、
冒頭の実績値/勘合長の設定(勘合長:d~2dで選択)と大体感覚に合う結果となる。
、、、が、そもそも締結においては摩擦係数自体のバラつきが大きいので、(軸力が思ったよりも発生せず)NGのはずが大丈夫なんて事もある。
補足として、ちょっとした設計配慮と材料の機械的性質の表をついでに、あと計算に使ったねじ山に作用する力についての注記。
その他補足
ちょっとした設計配慮
ねじの諸元をベースにした豆知識と設計配慮について
さて、当然ではあるが、同一締結箇所のおねじとめねじと勘合長は同じであれば、
”母材同士の強度が同一であれば、めねじ側より先に ”おねじ側のねじ山抜けが発生” する”
ようになっている。(もちろん、おねじの軸破断が先に発生しない前提)
これは、勘合長が同じであれば、めねじ側のせん断円はおねじより大きい事(d>D1)から、必然的にめねじ側のねじ山のせん断面積が大きくなるので、式を見なくても当たり前といえば当たり前
とはいうものの、①式と②式までずずーっと戻り、式で確認をすれば、
\(
\begin{align}
\tt F_{mN}&=\tt \displaystyle \frac{7\pi}{8}\cdot L_m\cdot d \cdot \tau_{BN} ・・・① \\[8pt]
\tt F_{mB}&=\tt \displaystyle \frac{3\pi}{4} \cdot L_m\cdot D_1 \cdot \tau_{BB}・・・②
\end{align}
\)
おねじ/めねじが同一強度 \((\tau_{BB}=\tau_{BN}) とすれば、\tt \displaystyle \frac{7\pi}{8}>\tt \frac{3\pi}{4} \) かつ \( \tt d >D_1 \) より、明らかに
\( \tt F_{mN}\ >\ \tt F_{mB} \)
である。
じゃぁ、どれぐらいの差?は以下(呼び径違いで算出)
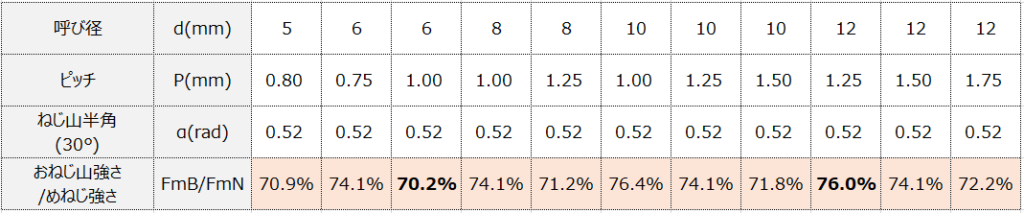
つまり、めねじのねじ山強度に対し、おねじのねじ山強度は大体2~3割減。差はこの程度。
という事は、、、逆にいえば、、、
おねじ側のせん断強さが強い場合(めねじ材に対し3割以上強ければ)、今度は ”めねじ側のねじ山抜け”が先に発生しはじめる。
(というか、材料強度差が大きい材料同士の締結は結構当たり前なので、結構おこる(アルミ鋳造部品へ高張力ボルトを使用した締結等々は最たる例かと)。)
これを避けたければ、勘合長を十分とり”ボルトの軸破断を先に起こす” 事を検討しておくのは、気の利いた設計配慮の一つとなる。
というのも、(作業不良等の)過大トルクで破損した場合、おねじ一本だけ壊れてくれた方が、コストも安い&交換も容易(作業復帰も早くなる)ため、ちょっとだけユーザーフレンドリー。
(上の計算例でいえば、No4->No5。もちろん、勘合長を十分にとっても、母材の組合せによっては、めねじが抜ける設定にしかできない場合もある(No5の例でも微妙))。
まぁ、設計上の制限を優先する場合もあるので、壊れ方の話をどこまで配慮するかは状況次第。
あくまでも過大トルク入力(= 作業不良)時の壊れざまの話であり、検討はしても結果はマストではない(かと)。
補足:材料の機械的性質
ネットで簡単に検索できるが、引張強さ&耐力のざっくりイメージ用に一覧で。
(正確な強度は使用する材料に応じてSpec確認要)
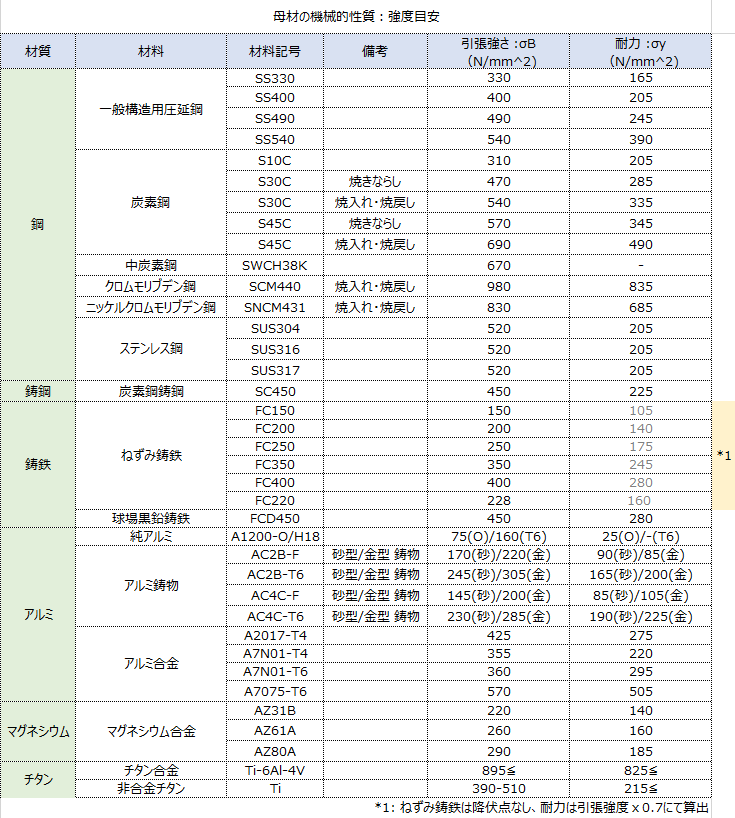
-> 自分はめねじの低強度材のイメージが200MPa程度以下ぐらいなので、念のために勘合長&締付けトルク設定とかちょっと気にするかな。。それ以上はねじ径分勘合長がとってあれば、何とかなるだろう的な。。。
注:ねじ山に作用する力
さてねじ山の破損時の荷重について今回はトルク法の最大発生軸力FsHを使ったが、参考書ではねじ山の破損時の荷重は以下で算出してある。
(参考書の計算では、最大軸力以上の荷重がねじ山にかかる計算になるので”あれ?”と思い、とりあえず計算には組み込まず。。)
まずは参考書そのままに。以下の図①の軸力 F からスタートして、力のつり合いから⑤をねじ山に作用する力 F’ として求める。(リード角0の近似とされている。)
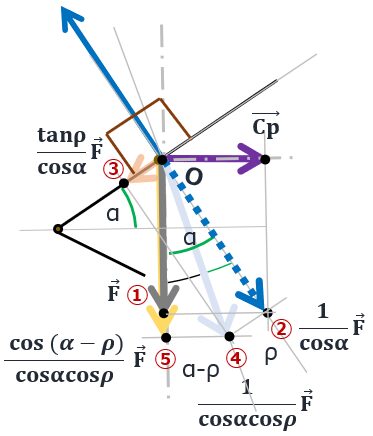
つまり、\( \tt F’=\displaystyle \frac{\cos(\alpha-\rho)}{\cos\alpha \cdot \cos\rho} F\)
上で使ったFsHをこのF’で置き換えればよい。より安全側になるので、参考書ベースであればFsHの代わりにこちらを。。



<ケースNo.1> おねじ:6.8級 / めねじ:SS540(だいたい同じの材料強度の想定)
勘合長はLm=dで計算
<ケースNo.2> おねじ:8.8級 / めねじ:AC4C(材料強度に差がある想定)
勘合長はLm=dで計算
(おねじ諸元のみでの締結トルク設定はNG)
<ケースNo.3> ケースNo.2に対して勘合長を伸ばして、Lm=1.5dで計算
<ケースNo.4> ケースNo.3に対して、おねじの強度区分をひとつあげて、10.9級で計算
<ケースNo.5> ケースNo.4に対して勘合長を伸ばして、Lm=2dで計算