- 二輪車の車両諸元の計算
- 式一覧
- \( \small{O – X_0Z_0} \) 座標系(計測セット位置) での ” Frアクスル座標 ” ((5)式は簡易版、(40)式は詳細版)
- \( \small{O – X_0Z_0} \) 座標系(計測セット位置) での “Rrアクスル座標“
- \( \small{O – X_0Z_0} \) 座標系 (計測セット位置) での ” グランドライン(G/L)の傾き “
- \( \small{O – X_0Z_0} \) 座標系 (計測セット位置) -> \( \small{O – X_1Z_1} \)座標系 (G/L基準) への ” 変換 “
- \( \small{O – X_1Z_1} \)座標系 (G/L基準) での ” キャスター角 “
- \( \small{O – X_1Z_1} \)座標系 (G/L基準) での ” ホイールベース長 “
- \( \small{O – X_1Z_1} \)座標系 (G/L基準) での ” トレール長 “
- \( \small{O – X_0Z_0} \) 座標系 (計測セット位置) ” H/P座標、点Bの座標 ” (長さ&高さ計測からの算出)
- 測定点の車両幅方向の補正
- ” キャスター角の算出 ” (長さ&高さ計測からの算出)
- パラメータ 一覧
- 式一覧
- グランドライン(地面)基準の車両諸元算出
- 追記
- さいごに
二輪車の車両諸元の計算
ベクトルを道具として使うとこんな計算もやりやすくなる、という例を。。。
ママチャリでは聞かないが、モーターサイクルにしろ競技用の自転車等で、操安向上目的にてフロント周りの変更(パーツ交換等にて)、サスペンションのセッティング変更を行う場合がある。で、変更する際に必要な情報の一つが、それにより操安性に影響するキャスター角、トレール、ホイールベースの値がどれぐらいが変わるか?の情報。
これをベクトルの内積計算 & 回転行列を使って計算。この計算はベクトルで考えると整理しやすい。
(内積、回転行列については以下を)
さて今回は、サスペンション(足回り)の変更に伴うキャスター角、トレール長、ホイールベース長の計算を主眼として、二次元で考える(転舵時の計算はまた今度)。
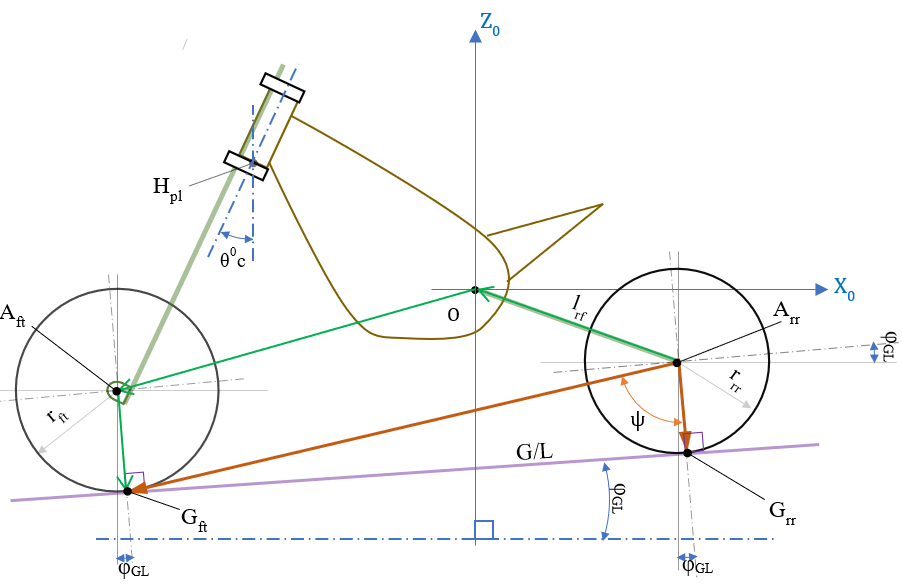
座標系を \( \small{O-X_0Z_0} \)(右手右ねじ系)とし、モデルの構成は以下とする。
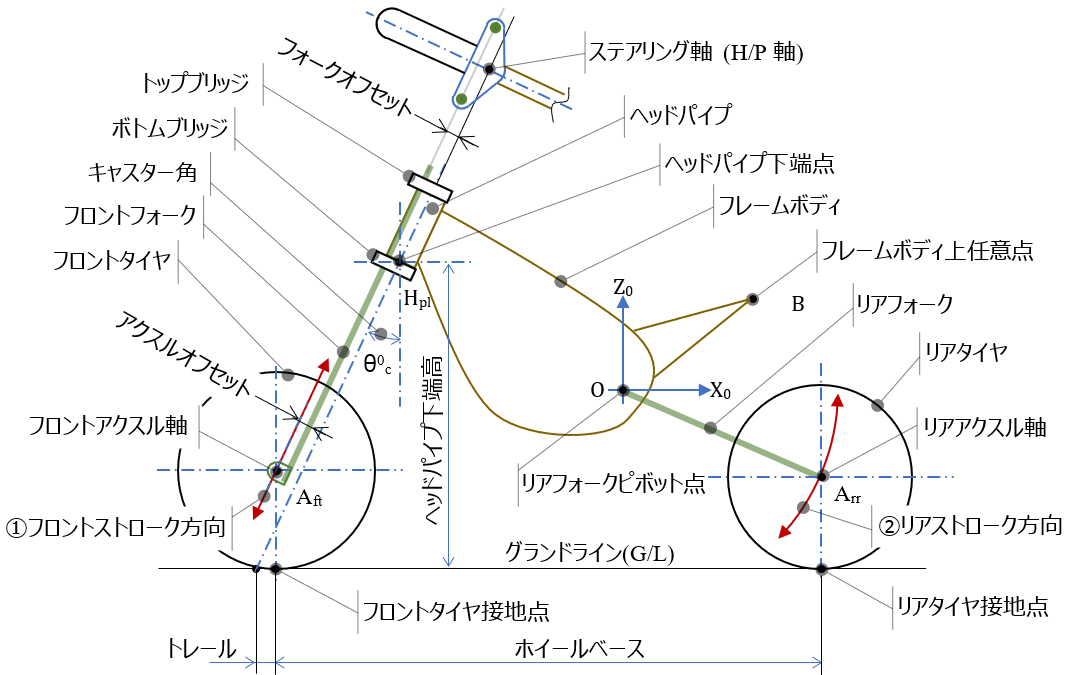
- フロントタイヤ(アクスル中心(点 \(A_{ft} \))を保持するフロントフォークは、トップブリッジ&ボトムブリッジを介してステアリング軸をもつフレームボディのヘッドパイプ(以下 \( \small{H/P} \) )にてフレームボディーに結合される
( \( \small{H/P} \) の下端点を点 \(H_{pl} \) とする) - リアタイヤ(アクスル中心(点 \(A_{rr} \)) を保持するリアフォークは、その回転のピボット点 にてフレームに結合される
- 座標系 \( \small{O-X_0Z_0} \) の原点 \(O \)にフレームボディーのリアフォークピボット点を設置し、キャスター角 \(θ^0_{c} \) にて\( \small{H/P} \) 下端高を設置し、フレームボディーを \( \small{O-X_0Z_0} \) に固定する(ばね上固定)。
(座標系 \( \small{O-X_0Z_0} \) 上にて、キャスター角 \(θ^0_{c} \) :フレームボディーの \( \small{H/P} \) 軸(ステアリング軸)と鉛直方向(\(Z_0 \) 軸平行)のなす角) - リアタイヤの位置はリアフォークのピボット点を中心とした回転方向(②)に沿ってのみ動く
- フロントタイヤの位置はフロントフォークの伸縮方向(①)に沿ってのみ動く
さて、フロントタイヤ接地点とリアタイヤ接地点を結ぶ線がグランドライン(地面基準の水平線:以下 \( \small{G/L} \))、また、ホイールベース長はこの二つの接地点の距離となる。
またトレール長は、\( \small{H/P} \) 軸を延長して \( \small{G/L} \) と交わる点と、フロントアクスルから \( \small{G/L} \) に投影した点との距離。
ばね上を固定しているので、サスペンションのストローク量が変われば \( \small{G/L} \) が変わる。
(ざっくりと言えば、ばね上(フレームボディー)を座標系 \( \small{O-X_0Z_0} \) に”固定”。サスペンションストロークに伴いばね下が動き \( \small{G/L} \) が動くモデルモデル)(下図)
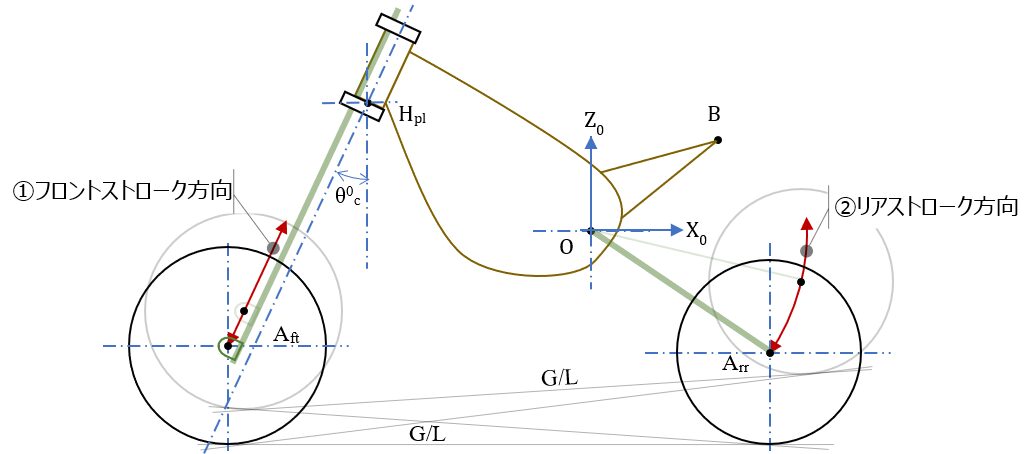
ホイールベース等の諸元変化の計算を目的としているので、ばね下だけを動かす方がベクトル計算の式がたてやすい。
式一覧
まずあらかじめ、算出した式一覧は、、
\( \small{O – X_0Z_0} \) 座標系(計測セット位置) での ” Frアクスル座標 ” ((5)式は簡易版、(40)式は詳細版)
\( \begin{align}
\left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft} \
\end{array} \right)
= & \left( \begin{array}{c}
x^ 0_{Hp}-l_{fs} \cdot sin \theta^0_{c} -(f_{off}+a_{off}) \cdot cos \theta^0_{c}\\
z^0_{Hp}-l_{fs} \cdot cos \theta^0_{c}+(f_{off}+a_{off}) \cdot sin \theta^0_{c}\
\end{array} \right)・・・\small{(5)} \\[6pt]
= & \left( \begin{array}{c}
x^0_{Hp}+ (t_{hp}+t_{tb}+ u_{ff}-l_{ff}+s_{fr}) \cdot sin \theta^0_{c}-(f_{off}+a_{off}) \cdot cos \theta^0_{c} \\
z^0_{Hp}+ (t_{hp}+t_{tb}+ u_{ff}-l_{ff}+s_{fr}) \cdot cos \theta^0_{c}+(f_{off}+a_{off}) \cdot sin \theta^0_{c} \
\end{array} \right) ・・・\small{(40)} \\
\end{align} \)
\( \small{O – X_0Z_0} \) 座標系(計測セット位置) での “Rrアクスル座標“
\( \left( \begin{array}{c}
x^0_{Arr} \\
z^0_{Arr} \
\end{array} \right)
= \dfrac{l_{rf}}{l_B} \cdot \left( \begin{array}{c}
cos φ_{Arr} \cdot x^0_{B} + sin φ_{Arr} \cdot z^0_{B}\\
– \ sin φ_{Arr} \cdot x^0_{B} + cos φ_{Arr} \cdot z^0_{B} \ \
\end{array} \right) \)・・・(14)
( \( cos φ_{Arr} \) = \( \dfrac{{l_B}^2+{l_{rf}}^2 – {l_{rs}}^2 }{2 \cdot l_B \cdot l_{rf}} \)、 \( sin φ_{Arr} \) = \( \sqrt{1- cos ^2 φ_{Arr}} \) )
\( \small{O – X_0Z_0} \) 座標系 (計測セット位置) での ” グランドライン(G/L)の傾き “
\( φ_{GL} = arcsin \dfrac{a_z}{\sqrt{a_x^2+a_z^2}} \ – \ arcsin \dfrac{a_r}{\sqrt{a_x^2+a_z^2}} \) ・・・(21-1)
(ここで、\(a_z= z^0_{Arr} – z^0_{Aft} \) 、\(a_x= x^0_{Arr} – x^0_{Aft} \) 、\( a_r=r_{rr} – r_{ft} \) )
\( \small{O – X_0Z_0} \) 座標系 (計測セット位置) -> \( \small{O – X_1Z_1} \)座標系 (G/L基準) への ” 変換 “
\( \left( \begin{array}{c}
x_{**} \\
z_{**} \
\end{array} \right) =\left( \begin{array}{c}
cos φ_{GL} \cdot x^0_{**} + sin φ_{GL} \cdot z^0_{**}\\
– sin φ_{GL} \cdot x^0_{**}+ cos φ_{GL} \cdot z^0_{**}\
\end{array} \right) \) ・・・(23)
\( \small{O – X_1Z_1} \)座標系 (G/L基準) での ” キャスター角 “
\(φ_{c} \) = \(θ^0_{c} + φ_{GL} \) ・・・(24)
\( \small{O – X_1Z_1} \)座標系 (G/L基準) での ” ホイールベース長 “
\( \begin{align}
wb &= cos φ_{GL} \cdot (x^0_{Arr}- x^0_{Aft}) + sin φ_{GL} \cdot ( z^0_{Arr}-z^0_{Aft}) ・・・\small{(27)} \\[6pt]
&= {\sqrt{a_x^2+a_z^2}} \ cos (α – φ_{GL}) ・・・\small{(28)}
\end{align} \)
( \(a_x \ , \ a_z \ , \ α \) は (21)式 と同じ )
\( \small{O – X_1Z_1} \)座標系 (G/L基準) での ” トレール長 “
\(\begin{align}
tr = & |(cos φ_{GL} \cdot x^0_{Aft} + sin φ_{GL} \cdot z^0_{Aft}) \\[6pt]
& \ – \ (cos φ_{GL} \cdot x^0_{HP} + sin φ_{GL} \cdot z^0_{HP}) \\[6pt]
& \ – \ (sin φ_{GL} \cdot x^0_{HP}\ – \ cos φ_{GL} \cdot z^0_{HP}) \cdot tan |({θ_{0c}+φ_{GL}}) | \\[6pt]
&+( sin φ_{GL} \cdot x^0_{Aft}\ – \ cos φ_{GL} \cdot z^0_{Aft}) \cdot tan |({θ_{0c}+φ_{GL}}) | \\[6pt]
&+r_{ft} \cdot tan |({θ_{0c}+φ_{GL}})|| ・・・\small{(37)}
\end{align} \)
\( \small{O – X_0Z_0} \) 座標系 (計測セット位置) ” H/P座標、点Bの座標 ” (長さ&高さ計測からの算出)
\( \left( \begin{array}{c}
x^0_{Hp} \\
z^0_{Hp} \
\end{array} \right) = \left( \begin{array}{c}
– \sqrt {{l_{HPl}}^2-(h^0_{Hp}-h^0_{O})^2 }\\
h^0_{Hp}-h^0_{O} \
\end{array} \right) \) ・・・(41)
\( \left( \begin{array}{c}
x^0_{B} \\
z^0_{B} \
\end{array} \right) = \left( \begin{array}{c}
\sqrt {{l_B}^2-(h^0_{B}-h^0_{O})^2 }\\
h^0_{B}-h^0_{O} \
\end{array} \right) \) ・・・(42)
測定点の車両幅方向の補正
\(l_{xx}= \sqrt{{l_{act}}^2- {l_{adj}}^2}) \) ・・・(43)
” キャスター角の算出 ” (長さ&高さ計測からの算出)
\( \theta^0_{c} = arccos( \dfrac{h^0_{Hp} \ – \ h^0_{A0ft}}{\sqrt{l_{fs}^2+(f_{off}+a_{off})^2}}) \ – \ arccos( \dfrac{l_{fs}}{\sqrt{l_{fs}^2+(f_{off}+a_{off})^2}} ) \) ・・・(48-1)
パラメータ 一覧
この計算式を使ったツールはこちらで。
で、算出の詳細は以下にて、
グランドライン(地面)基準の車両諸元算出
計算の流れ
諸元計算の流れは、(以下 フロント: Fr、リア :Rrにて表記 )
- Step1: フレームボディ(ばね上)を固定させた座標系 \( \small{O-X_0Z_0} \) にて、H/P下端点基準にFrアクスル位置を算出
Note: H/P下端点をFrストローク量算出の測定基準点に使用 - Step2: 同様にフレームボディ後端あたりにある任意の点Bを基準にRrアクスル位置を算出
Note1: 任意点B:リアストローク算出の測定基準点
Note2: Rrタイヤは原点O周りの回転方向移動であり、点BとRrアクスルの距離はリアストローク量とは一致はしない。
((角度より)長さの方が実測しやすいため、Rrストローク量算出の基準点代用として設定) - Step3:そのアクスル位置におけるFr&Rrタイヤの接線から\( \small{G/L} \) の角度 \(φ_{GL} \) を算出
- Step4: 算出した\(φ_{GL} \) を使った回転行列 \(R_{φ_{GL}} \) により \( \small{O-X_0Z_0} \) を丸ごと回転させ、新しい座標系 \( \small{O-X_1Z_1} \) に変換。
- Step5: 変化後の各車両各諸元値を、\( \small{O-X_1Z_1} \) の座標系にて算出
要は、 \( \small{O-X_0Z_0} \) での \( \small{G/L} \) の傾き \(φ_{GL} \) を使いモデルごと回転させれば、回転後の座標系 \( \small{O-X_1Z_1} \) では \( \small{G/L} \) は水平になる。
これを使って(タイヤ位置がどこであれ)\( \small{O-X_1Z_1} \) 上から読み取れば、車両の各諸元値はその座標値、もしくは簡単な足し算引き算で求められる、という感じ
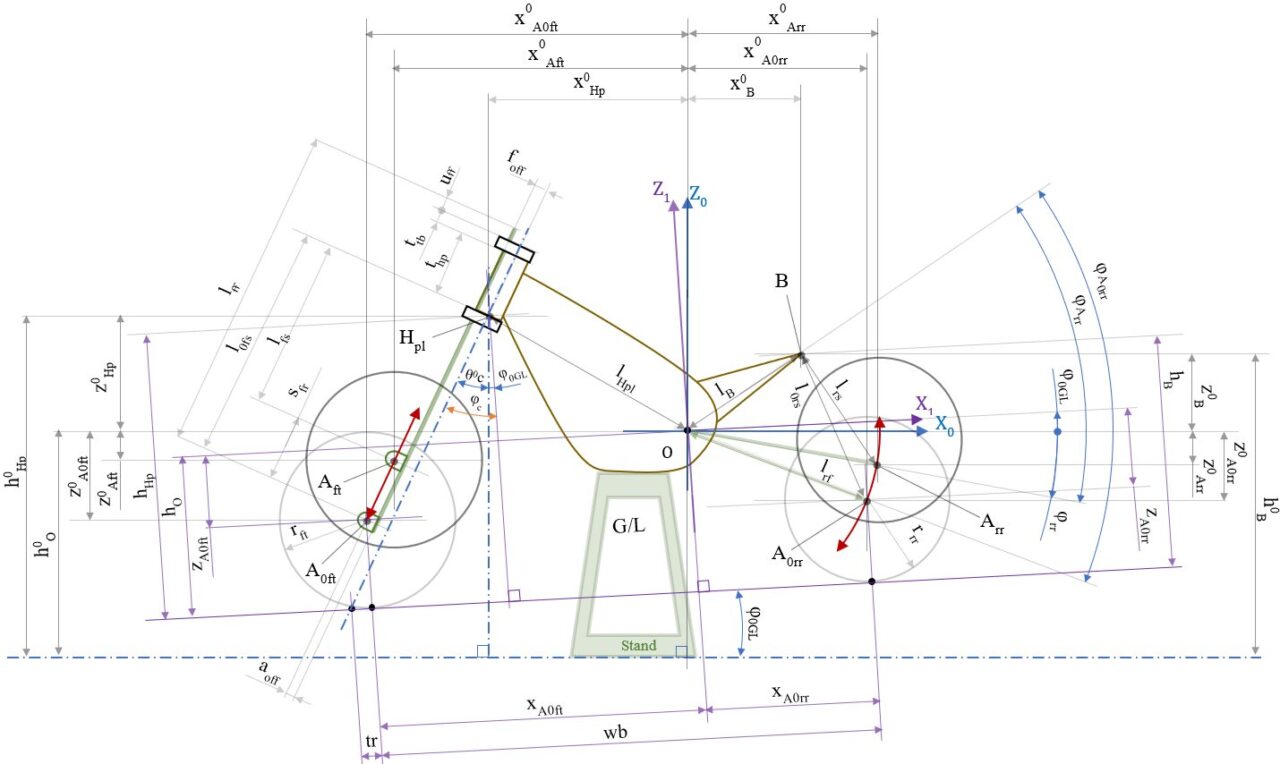
設定したパラメータ名一覧を一旦以下に

\(O \) : Rrフォークピボット点(原点)
\(h^0_{O} \) : Rrフォークピボット高 \(^{*(1)} \)
\(h_{O} \) : Rrフォークピボット高
\(H_{pl} \) : H/P下端点位置
\(h^0_{Hp} \) : H/P下端点高 \(^{*(1)} \)
\(h_{Hp} \) : H/P下端点高
\(l_{Hpl} \) : H/P下端点-原点 \(O \) の距離
\(t_{hp} \) : H/P長
\(t_{tb} \) : トップブリッジ厚
\(u_{ff} \) : Frフォーク 突出し量
\(l_{ff} \) : Frフォーク長(初期設置位置)
\(s_{fr} \) : Frフォーク ストローク量
\(l_{fs} \) : H/P下端面とFrアクスルの距離
\(l_{0fs} \) : 初期設置位置でのH/P下端面とFrアクスルの距離
\(f_{off} \) : フォークオフセット長
\(a_{off} \) : アクスルオフセット長
\(A_{ft} \) : Frアクスル軸位置
\(A_{0ft} \) : Frアクスル軸初期位置
\(r_{ft} \) : Frタイヤ半径
\(B \) : (ばね上の)フレームボディ上の任意点\( ^{*(5)} \)
\(h^0_{B} \) : 点B高 \(^{*(1)} \)
\(h_{B} \) : 点B高
\(l_{B} \) : 点B-原点 \(O \) の距離
\(A_{rr} \) : Rrアクスル軸位置
\(A_{0rr} \) : Rrアクスル軸初期位置
\(r_{rr} \) : Rrタイヤ半径
\(l_{rf} \) : Rrフォーク長
\(φ_{Arr} \) : \(OA_{rr} \)と \(OB \) 軸のなす角 \(^{*(3)} \)
\(φ_{0Arr} \) : \(OA_{0rr} \)と \(OB \) 軸のなす角 \(^{*(3)} \)
\(l_{rs} \) : 点\(\small{B} \) と 点 \(\small{A_{rr}} \) 間の長さ(Rrストローク長代用)
\(l_{0rs} \) : 点\(\small{B} \) と 点 \(\small{A_{0 rr}} \) 間の長さ(Rrストローク全伸長代用)
\(tr \) : トレール長(G/L基準)
\(wb \) : ホイールベース長(G/L基準)
\(φ_{GL} \) : G/L角 \(^{*(3)} \) \(^{*(4)} \)
\(φ_{0GL} \) : 初期位置におけるG/L角 \(^{*(3)} \) \(^{*(4)} \)
\(θ^0_{c} \) : キャスター角 \(^{*(2)} \)
\(φ_{c} \) : キャスター角(G/L基準)
\( ^{*(1)} \) : 初期セット値 (\( \small{O_0-X_0Z_0} \) 上)
\( ^{*(2)} \)\(θ_{**} \) : 角度定数 \(θ_{**}>0 \)
\( ^{*(3)} \)\(φ_{**} \) : 角度変数 \(φ_{**} \)の向きは右ねじ方向正
\( ^{*(4)} \) : \( – \dfrac{\pi}{2} ≦φ_{GL} ≦ \dfrac{\pi}{2} \)
\( ^{*(5)} \) : Rrサスペンション全屈時のアクスル位置より上
Note1:ここでのパラメータ各値は図③モデルに従った正か0を想定しているが、負の値をとるのも可 (アクスルオフセット値が図③モデルと逆方向で、負になるとか)。
Note2:\( \small{O-X_0Z_0} \) 座標系は右手&右ねじで設定し、計算時の正負はそれに従う
Note3:\( \small{O-X_0Z_0} \)座標のパラメータは添字右上に”0”を追記 : \( x^{\color{red}{0}}_{y} \)
-> 車両をスタンドに乗せたフロント&リアサス全伸び状態からモデル作成開始
フロントアクスル位置の算出 (Step1)
(計算 Step1)
座標系は \( \small{O-X_0Z_0} \) を使用
Frアクスル位置( \( \small{\overrightarrow{OA_{ft}}}\) )は、図④の赤矢印ルート上にあるベクトルがその位置算出に使用するベクトルとなるが、これは単に点をなぞっていくだけの単純なベクトルの足し算
\(\overrightarrow{OA_{ft}} = \overrightarrow{OH_{pl}} +\overrightarrow{H_{pl}J}+\overrightarrow{JL}+\overrightarrow{LA_{ft}}\) ・・・(1)
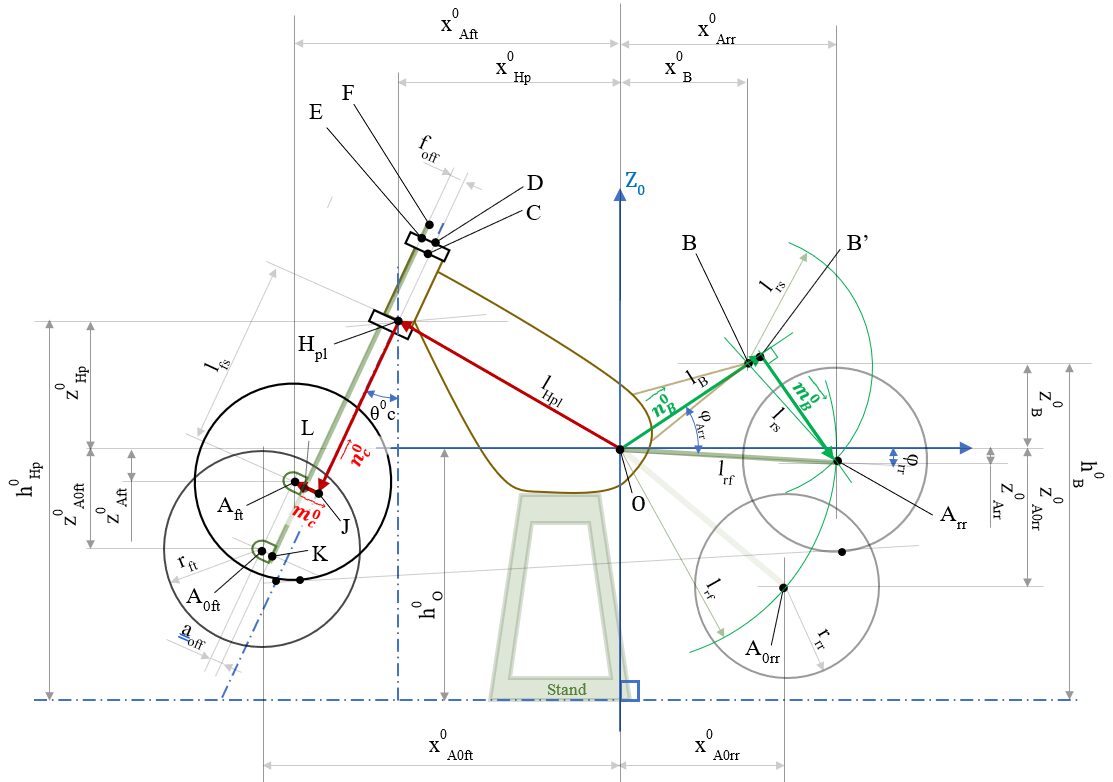
ここで
- \( \overrightarrow{n^0_{c}} \):キャスター角下向きの方向ベクトル ( \( \vert \overrightarrow{n^0_{c}} \vert \) = 1:単位ベクトル)
- \( \overrightarrow{m^0_{c}} \):フロントアクスル方向にむかい、\( \overrightarrow{n^0_{c}} \) に直交する単位ベクトル ( \( \vert \overrightarrow{m^0_{c}} \vert \) = 1:単位ベクトル)
の二つのベクトルを設定する。
これらと図③の各パラメータ値を使い①式を書き直せば、フロントアクスル位置を示す \( \small{\overrightarrow{OA_{ft}}}\) は
\( \begin{align}
\overrightarrow{OA_{ft}}
= & \overrightarrow{OH_{pl}} +l_{fs} \cdot \overrightarrow{n^0_{c}} +f_{off}\cdot \overrightarrow{m^0_{c}} +a_{off} \cdot \overrightarrow{m^0_{c}} \\
= & \overrightarrow{OH_{pl}}+l_{fs} \cdot \overrightarrow{n^0_{c}} +(f_{off}+a_{off}) \cdot \overrightarrow{m^0_{c}} \ ・・・(2)
\end{align} \)
あとはこれを座標に落とし込めばよい。
まず、\( \vec{n^0_{c}} \) はキャスター角下向き方向の単位ベクトルより、
\( \overrightarrow{n^0_{c}} \) =\( \left( \begin{array}{c}
cos-(\dfrac{\pi}{2} +\theta^0_{c}) \\
sin-(\dfrac{\pi}{2} +\theta^0_{c} ) \
\end{array} \right) \) = \(- \left( \begin{array}{c}
sin \theta^0_{c} \\
cos \theta^0_{c} \
\end{array} \right) ・・・(3) \)
\( \overrightarrow{m^0_{c}} \) 、\( \overrightarrow{n^0_{c}} \)は互いに直行から \( \overrightarrow{m^0_{c}} \cdot \overrightarrow{n^0_{c}} =0 \) 。
これに向きと \( \overrightarrow{m^0_{c}} \) は単位ベクトルである事を踏まえれば、
\( \overrightarrow{m^0_{c}} \) = \( \left( \begin{array}{c}
-cos \theta^0_{c} \\
sin \theta^0_{c} \
\end{array} \right) ・・・(4) \)
(3)(4)のベクトルを使い、\( \overrightarrow{OA_{ft}}
= \left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft} \
\end{array} \right) \) 、 \( \overrightarrow{OH_{pl}}
= \left( \begin{array}{c}
x^0_{Hp} \\
z^0_{Hp} \
\end{array} \right) \) とすれば、(2)式 は、
\( \begin{align}
\overrightarrow{OA_{ft}}
= \left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft} \
\end{array} \right)
= & \left( \begin{array}{c}
x^0_{Hp} \\
z^0_{Hp} \
\end{array} \right) \
+l_{fs} \cdot – \left( \begin{array}{c}
sin \theta^0_{c} \\
cos \theta^0_{c} \
\end{array} \right) \
+(f_{off}+a_{off}) \cdot \left( \begin{array}{c}
-cos \theta^0_{c} \\
sin \theta^0_{c} \
\end{array} \right)\\[8pt]
= & \left( \begin{array}{c}
x^ 0_{Hp}-l_{fs} \cdot sin \theta^0_{c} -(f_{off}+a_{off}) \cdot cos \theta^0_{c}\\
z^0_{Hp}-l_{fs} \cdot cos \theta^0_{c}+(f_{off}+a_{off}) \cdot sin \theta^0_{c}\
\end{array} \right) ・・・(5) \
\end{align} \)
となり、これが、\( \small{O-X_0Z_0} \) における 原点\(\small{O} \) からFrアクスル位置へのベクトル成分値(座標値)。
リアアクスル位置算出 (Step2)
(計算 Step2)
座標系は \( \small{O-X_0Z_0} \) を使用
座標系 \( \small{O-X_0Z_0} \) 上のRrアクスル位置 \( \left( \begin{array}{c}
x^0_{Arr} \\
z^0_{Arr} \
\end{array} \right) ( = \overrightarrow{OA_{rr}} \) ) はシンプルに、
\( \overrightarrow{OA_{rr}}\) = \(\left( \begin{array}{c}
x^0_{Arr} \\
z^0_{Arr}\
\end{array} \right) \) = \( l_{rf} \cdot\left( \begin{array}{c}
cos φ_{rr} \\
sin φ_{rr} \
\end{array} \right) ・・・(6)\)
でもよいが、ストロークによるRrフォークの角度変化を追いかけるのも一苦労なので、長さ測定で車両諸元変化が算出できるように、ひと手間。

Rrサスペンション全屈時のアクスル位置より上にとったばね上(フレームボディ上)の固定点B \(\left( \begin{array}{c}
x^0_{B} \\
z^0_{B} \
\end{array} \right) \) をRrストローク長測定の代用基準点として使う事にする。
OBの延長上の(∠\(\small{OB’A_{rr}}=\dfrac{\pi}{2} \) ) となる点をB’点 として、
\( \overrightarrow{OA_{rr}} \) = \( \overrightarrow{OB’}+\overrightarrow{B’A_{rr}} \) ・・・(7)
とみた 図④ の緑矢印ルート上にあるベクトルが、Rrアクスル位置に算出に使用するベクトル。
さて、まずは各ベクトルの方向を求める。
点B’はOBの延長線上である事を踏まえれば、\( \small{\overrightarrow{OB’}} \) 方向の単位ベクトル \( \overrightarrow{n^0_{B}} \) は、
\( \overrightarrow{n^0_{B}} \) = \( \dfrac{1}{l_B}\left( \begin{array}{c}
x^0_{B} \\
z^0_{B} \
\end{array} \right) \) ・・・(8)
また、\( \small{\overrightarrow{OB’}} \) に対して 法線方向である\( \small{\overrightarrow{B’A_{rr}}} \)の単位ベクトル\( \overrightarrow{m^0_{B}} \) は、方向をふまえれば
\( \overrightarrow{m^0_{B}} \) = \( \dfrac{1}{l_{B}}\left( \begin{array}{c}
z^0_{B} \\
-x^0_{B} \
\end{array} \right) \) ( ∵ \( \overrightarrow{m^0_{B}} \cdot \overrightarrow{n^0_{B}} =0 \) ) ・・・(9)
次は各ベクトルの長さを求める。
まずは、長さ算出に使用する角 \( \small{∠BOA_{rr}} \) ( 以下 \( φ_{Arr} \) ) を求めてみる。
三角形 ⊿\(\small{OBA_{rr}} \) に着目すれば、3辺はわかっているので、\( φ_{Arr} \) に余弦定理が使える。つまり、
\( cos φ_{Arr} \) = \( \dfrac{{l_B}^2+{l_{rf}}^2 – {l_{rs}}^2 }{2 \cdot l_B \cdot l_{rf}} \) ・・・(10)
ついでに \( sin φ_{Arr} \) は、\( 0 ≦ φ_{Arr} ≦ \pi \) とすれば \( sin φ_{Arr} ≧ 0 \)、よって
\( sin φ_{Arr} \) = \( \sqrt{1- cos ^2 φ_{Arr}} \) ・・・(11)
Note:計算式の簡易化のため、以降の式内では \( cos φ_{Arr} \)、\( sin φ_{Arr} \) これ以上展開せずそのまま使用(cos/sin値の算出自体は、エクセル等の計算ソフトにお任せ。一旦算出してから他の式に適用。)
さて、ひき続いて直角三角形 ⊿\(\small{OB’A_{rr}} \) に着目し、上のcos値、sin値を使えばそれぞれ
(8)(9)(10)(11)より、(7)式は
\( \begin{align}
\overrightarrow{OA_{rr}} = \left( \begin{array}{c}
x^0_{Arr} \\
z^0_{Arr} \
\end{array} \right)
&= \overrightarrow{OB’}+\overrightarrow{B’A_{rr}} \\[6pt]
& =cos φ_{Arr} \cdot l_{rf} \cdot \dfrac{1}{l_B}\left( \begin{array}{c}
x^0_{B} \\
z^0_{B} \
\end{array} \right)
+ sin φ_{Arr} \cdot l_{rf} \cdot \dfrac{1}{l_{B}} \left( \begin{array}{c}
z^0_{B} \\
-x^0_{B} \
\end{array} \right) \\[6pt]
& = \dfrac{l_{rf}}{l_B} \cdot \left( \begin{array}{c}
cos φ_{Arr} \cdot x^0_{B} + sin φ_{Arr} \cdot z^0_{B}\\
– \ sin φ_{Arr} \cdot x^0_{B} + cos φ_{Arr} \cdot z^0_{B} \ \
\end{array} \right) ・・・\small{(14)}
\end{align} \)
( ここで、\( cos φ_{Arr} \) = \( \dfrac{{l_B}^2+{l_{rf}}^2 – {l_{rs}}^2 }{2 \cdot l_B \cdot l_{rf}} \)、 \( sin φ_{Arr} \) = \( \sqrt{1- cos ^2 φ_{Arr}} \) )
となり、これが、\( \small{O-X_0Z_0} \) における 原点\(\small{O} \) から(点B経由の)Rrアクスル位置へのベクトル成分値(座標値)
(14)式追記。。というのも、求めるのに遠回りし過ぎた。。。この式、よく見れば
\( \begin{align}
\overrightarrow{OA_{rr}} = \left( \begin{array}{c}
x^0_{Arr} \\
z^0_{Arr} \
\end{array} \right)
& = \dfrac{l_{rf}}{l_B} \cdot \left( \begin{array}{c}
cos φ_{Arr} \cdot x^0_{B} + sin φ_{Arr} \cdot z^0_{B}\\
– \ sin φ_{Arr} \cdot x^0_{B} + cos φ_{Arr} \cdot z^0_{B} \ \
\end{array} \right) \\[6pt]
& = \dfrac{l_{rf}}{l_B} \cdot \begin{pmatrix}
cos (- φ_{Arr}) & – sin (- φ_{Arr})\\
sin (- φ_{Arr}) & cos (- φ_{Arr}) \ \
\end{pmatrix} \left( \begin{array}{c}
x^0_{B} \\
z^0_{B} \
\end{array} \right)
\end{align} \)
この 2X2行列部分を \( R_{φ_{Arr}} \) とすれば 、これはベクトルを \( – φ_{Arr} \) だけ回転させる回転行列。
よってこの式は、
\( \overrightarrow{OA_{rr}}= \dfrac{l_{rf}}{l_B} \cdot R_{φ_{Arr}} \cdot \overrightarrow{OB} \) ・・・(14-1)と書ける。
つまり、ベクトル \( \overrightarrow{OB} \) を \( – φ_{Arr} \) 回転させて、大きさを \(\dfrac{l_{rf}}{l_B} \) 倍すれば、Rrアクスルへのベクトル \( \overrightarrow{OA_{rr}} \) ですよと。
(14-1)式から解く方がよっぽど素直、というか普通か。。。
(まぁ、いろいろな求め方があるという事でご勘弁。)
グランドライン(G/L)の傾き算出 (Step3)
(計算 Step3)
さて、ここまでで求めたFrアクスル座標、Rrアクスル座標は、式の簡易化のため以降の記載では以下のまま。
Frアクスル軸:\( \overrightarrow{O_0A_{ft}} = \left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft} \
\end{array} \right) \) 、Rrアクスル軸:\( \overrightarrow{OA_{rr}} = \left( \begin{array}{c}
x^0_{Arr} \\
z^0_{Arr} \
\end{array} \right) \)
さて新たに、Frタイヤの接地点を点 \( G_{ft} \), Rrタイヤの接地点を点 \( G_{rr} \) を設定して、前後各アクスル軸から各接地点へのベクトルを見れば、
\( \overrightarrow{A_{rr}G_{rr}} \) = \( r_{rr} \cdot\left( \begin{array}{c}
cos (-\dfrac{\pi}{2}+φ_{GL}) \\
sin (-\dfrac{\pi}{2}+φ_{GL}) \
\end{array} \right) \) = \( r_{rr} \cdot\left( \begin{array}{c}
sin φ_{GL} \\
-cos φ_{GL} \
\end{array} \right) \) ・・・(15)
\( \overrightarrow{A_{ft}G_{fr}} \) = \( r_{fr} \cdot\left( \begin{array}{c}
cos (-\dfrac{\pi}{2}+φ_{GL}) \\
sin (-\dfrac{\pi}{2}+φ_{GL}) \
\end{array} \right) \) = \( r_{ft} \cdot\left( \begin{array}{c}
sin φ_{GL} \\
-cos φ_{GL} \
\end{array} \right) \) ・・・(16)
である。また、G/LはFrタイヤ&Rrタイヤの双方の接線が故、(15)(16)ベクトルはG/Lに直角、つまり
\( \overrightarrow{A_{rr}G_{rr}} \cdot \overrightarrow{G_{rr}G_{ft}} =\overrightarrow{A_{ft}G_{ft}} \cdot \overrightarrow{G_{ft}G_{rr}} =0 \)
さてこれに、Frのタイヤ半径( \( r_{ft} \) )とRrのタイヤ半径( \( r_{rr} \) )を使えば、Fr&Rrタイヤの任意の位置における\( \small{O-X_0Z_0} \) 上のG/L の傾き \( φ_{GL} \) が算出できる。
まず、直角三角形 ⊿\( A_{rr}G{rr}G_{ft} \) に着目する。(Fr/Rr どちらでも構わないが、ココではRr側を使う)
G/LはFrタイヤ&Rrタイヤの双方の接線となる事、またベクトルの内積は投影である事を利用すれば、Rrアクスルを基点にもつ二つのベクトル \( \overrightarrow{A_{rr}G_{rr}} \) と \( \overrightarrow{A_{rr}G_{ft}} \) の内積は(ベクトル同士のなす角は \( ψ \) )、
\( \begin{align}
\overrightarrow{A_{rr}G_{rr}} \cdot \overrightarrow{A_{rr}G_{ft}} &= |\overrightarrow{A_{rr}G_{rr}}| \cdot \ |\overrightarrow{A_{rr}G_{ft}}| \cdot cos ψ \\[6pt]
&= r_{rr}\cdot r_{rr} \\[6pt]
&= r_{rr}^2 ・・・(17) \\[6pt]
\end{align} \)
(∵ \( ∠A_{rr}G_{rr}G_{ft}=\dfrac{\pi}{2}\) より、\(|\overrightarrow{A_{rr}G_{ft}}| \cdot cos ψ= r_{rr}) \)
が成立している事がわかる(図⑥の橙ベクトル同士の内積)。これを利用する(注記あり)。
図⑥の緑ルート上のベクトルに分解すれば
\( \begin{align}
r_{rr}^2 = \overrightarrow{A_{rr}G_{rr}} \cdot \overrightarrow{A_{rr}G_{ft}} &= ( \overrightarrow{A_{ft}G_{ft}} \ + \ \overrightarrow{OA_{ft}} \ – \ \overrightarrow{OA_{rr}} ) \cdot \overrightarrow{A_{rr}G_{rr}}\\[6pt]
&= \overrightarrow{A_{ft}G_{ft}} \cdot \overrightarrow{A_{rr}G_{rr}} \ + \ \overrightarrow{OA_{ft}} \cdot \overrightarrow{A_{rr}G_{rr}} \ – \ \overrightarrow{OA_{rr}} \cdot \overrightarrow{A_{rr}G_{rr}}・・・(18)
\end{align} \)
これに成分値をいれれば、\( φ_{GL} \) (\( – \dfrac{\pi}{2} ≦φ_{GL} ≦ \dfrac{\pi}{2} \) ) に関する関係式が出てくる。つまり、
\( \begin{align}
r_{rr}^2 &= \overrightarrow{A_{ft}G_{ft}} \cdot \overrightarrow{A_{rr}G_{rr}} \ + \ \overrightarrow{OA_{ft}} \cdot \overrightarrow{A_{rr}G_{rr}} \ – \ \overrightarrow{OA_{rr}} \cdot \overrightarrow{A_{rr}G_{rr}} \\[8pt]
r_{rr}^{\cancel{2}} &= r_{ft} \cdot \left( \begin{array}{c}
sin φ_{GL} \\
-cos φ_{GL} \
\end{array} \right) \cdot \cancel{r_{rr}} \cdot \left( \begin{array}{c}
sin φ_{GL} \\
-cos φ_{GL} \
\end{array} \right) \\[8pt]
&+ \left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft}\
\end{array} \right) \cdot \cancel{r_{rr}} \cdot \left( \begin{array}{c}
sin φ_{GL} \\
-cos φ_{GL} \
\end{array} \right) \ – \ \left( \begin{array}{c}
x^0_{Arr} \\
z^0_{Arr}\
\end{array} \right) \cdot \cancel{r _{rr}} \cdot \left( \begin{array}{c}
sin φ_{GL} \\
-cos φ_{GL} \
\end{array} \right) \\[8pt]
&= r_{ft} \cdot (sin^2 φ_{GL} + cos^2 φ_{GL} )
+ ( x^0_{Aft} \cdot sin φ_{GL} – z^0_{Aft} \cdot cos φ_{GL} )
– ( x^0_{Arr} \cdot sin φ_{GL} \ – \ z^0_{Arr} \cdot cos φ_{GL}) \\[8pt]
&= r_{ft}
\ – \ ( x^0_{Arr} – x^0_{Aft} ) \cdot sin φ_{GL}
+ ( z^0_{Arr} – z^0_{Aft} ) \cdot cos φ_{GL}
\end{align} \)
つまり、
\( ( z^0_{Arr} – z^0_{Aft} ) \cdot cos φ_{GL} \ – \ ( x^0_{Arr} – x^0_{Aft}) \cdot sin φ_{GL}
= (r_{rr} \ – \ r_{ft}) \)
ここで、\(a_z= z^0_{Arr} – z^0_{Aft} \) , \(a_x= x^0_{Arr} – x^0_{Aft} \) , \( a_r=r_{rr} – r_{ft} \) とおけば、これは
\( a_z\cdot cos φ_{GL} \ – \ a_x \cdot sin φ_{GL} = a_r \) ・・・(19)
であり、 \( sin α = \dfrac{a_z}{\sqrt{a_x^2+a_z^2}} \) , \( cos α = \dfrac{a_x}{\sqrt{a_x^2+a_z^2}} \) となる角度αを設定すれば、正弦の加法定理が使える。
つまり、(19)式は
\( {\sqrt{a_x^2+a_z^2}} (sin α \cdot cos φ_{GL} \ – \ cos α \cdot sin φ_{GL}) = a_r \) となり
\( sin (α – φ_{GL}) = \dfrac{a_r}{\sqrt{a_x^2+a_z^2}} \) ・・・(20)
となる。これから
\( α – φ_{GL} = arcsin( \dfrac{a_r}{\sqrt{a_x^2+a_z^2}}) \)
よって、
\( φ_{GL} = α \ – \ arcsin \dfrac{a_r}{\sqrt{a_x^2+a_z^2}} \) ・・・(21)
\(α \) は、\( sin α = \dfrac{a_z}{\sqrt{a_x^2+a_z^2}} \) より \( α = arcsin \dfrac{a_z}{\sqrt{a_x^2+a_z^2}} \) を使えば
\( φ_{GL} = arcsin \dfrac{a_z}{\sqrt{a_x^2+a_z^2}} \ – \ arcsin \dfrac{a_r}{\sqrt{a_x^2+a_z^2}} \) ・・・(21-1)
により \( φ_{GL} \) が求まる。式から見ての通り、タイヤ径が同じ (\( a_r=0 \)) であれば前後アクスル軸の位置の差がそのままG/Lの傾き(まぁ、当然か。。)
注記1:角度αについて
(20)式がシンプルになったので、あれ?と思い図で確認。
計算前に一旦下の図に気づいていれば、ベクトル計算は不要だったかもなぁと。。。G/Lの角度出すだけだし。。。
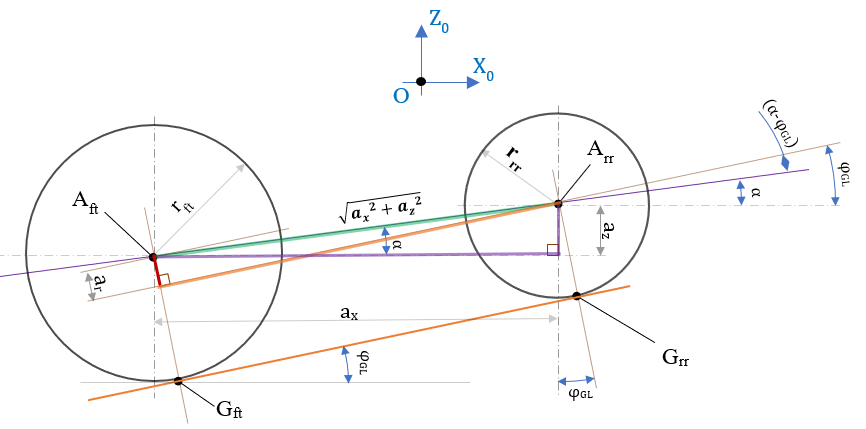
ちゃんちゃん。。と。
(まぁ、思いつかなくてもベクトル使えば求まるという事で。。)
G/Lを基準とした座標系とその変換: (Step4)
(計算 Step4)
さて、算出した\(φ_{GL} \) を使った回転行列 \(R_{φ_{GL}} \) で \( \small{O-X_0Z_0} \) を変換すれば、G/Lを基準とした新規座標系 \( \small{O-X_1Z_1} \) が設定できる。(= 任意位置の前後タイヤの接線を結んだG/Lを基準にした座標系。)
回転行列 \(R_{φ_{GL}} \) は、\(R_{φ_{GL}} \) = \( \begin{pmatrix}
cos φ_{GL} & sin φ_{GL} \\
– sin φ_{GL} & cos φ_{GL}
\end{pmatrix} \) ・・・(22) であることから、
もとの座標系 \( \small{O-X_0Z_0} \)上の任意点 \( (x^0_{**}, z^0_{**}) \) を \( \small{O-X_1Z_1} \) 上へ変換した点 \( (x_{**}, z_{**}) \) は、
\( \begin{align}
\left( \begin{array}{c}
x_{**} \\
z_{**} \
\end{array} \right) &= R_{φ_{GL}} \left( \begin{array}{c}
x^0_{**} \\
z^0_{**} \
\end{array} \right) = \begin{pmatrix}
cos φ_{GL} & sin φ_{GL} \\
– sin φ_{GL} & cos φ_{GL}
\end{pmatrix} \left( \begin{array}{c}
x^0_{**} \\
z^0_{**} \
\end{array} \right) \\[8pt]
&= \left( \begin{array}{c}
cos φ_{GL} \cdot x^0_{**} + sin φ_{GL} \cdot z^0_{**}\\
– sin φ_{GL} \cdot x^0_{**}+ cos φ_{GL} \cdot z^0_{**}\
\end{array} \right) ・・・\small{(23)}
\end{align} \)
これが変換のベース。これに後はベクトルの足し算引き算で、G/L基準の座標系での車両諸元値が求まる。
(回転行列詳細については、以下の記事に)
G/L基準の車両諸元算出 (Step5)
(計算の流れ:Step5)
G/L基準のキャスター角
さてここまでこれば、あと少し。まずは、以下の図⑦をベースに。
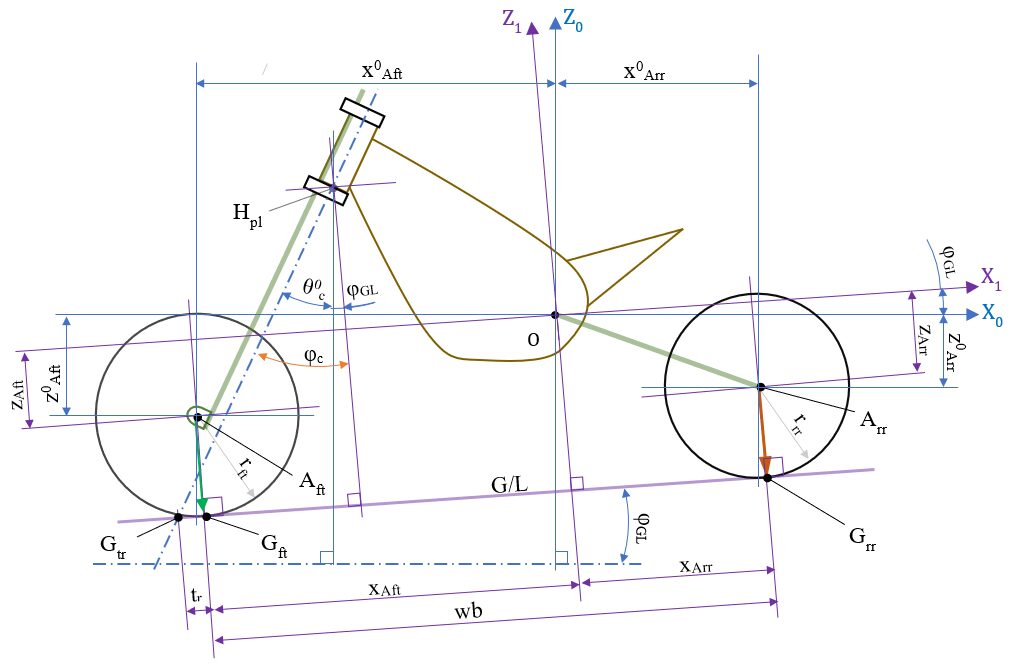
\( \small{O-X_1Z_1} \) 上でのキャスター角 \(φ_{c} \) は、\( \small{O-X_0Z_0} \) での \(θ^0_{c} \) に \( φ_{GL}\) を足すだけ。
\(φ_{c} \) = \(θ^0_{c} + φ_{GL} \) ・・・(24)
G/L基準のホイールベース計算
(5)式で使った Frアクスル座標 \( \left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft} \
\end{array} \right) \), (14)式で使った Rrアクスル座標 \( \left( \begin{array}{c}
x^0_{Arr}\\
z^0_{Arr} \
\end{array} \right) \) を使う。
(共に \( \small{O-X_0Z_0}\) 上の座標 )
ここで、\( \small{O-X_1Z_1} \) 上での Frアクスル座標を \( \left( \begin{array}{c}
x_{Aft} \\
z_{Aft} \
\end{array} \right) \) 、Rrアクスル座標を \( \left( \begin{array}{c}
x_{Arr} \\
z_{Arr} \
\end{array} \right) \) とすれば、(23)式をつかって
\( \begin{align}
\left( \begin{array}{c}
x_{Aft} \\
z_{Aft} \
\end{array} \right) &= R_{φ_{GL}} \left( \begin{array}{c}
x^0_{Aft}\\
z^0_{Aft} \
\end{array} \right) \\[6pt]
&= \left( \begin{array}{c}
cos φ_{GL} \cdot x^0_{Aft} + sin φ_{GL} \cdot z^0_{Aft}\\
– sin φ_{GL} \cdot x^0_{Aft} + cos φ_{GL} \cdot z^0_{Aft}\
\end{array} \right) ・・・(25)
\end{align} \)
\( \begin{align}
\left( \begin{array}{c}
x_{Arr} \\
z_{Arr} \
\end{array} \right) &= R_{φ_{GL}} \left( \begin{array}{c}
x^0_{Arr}\\
z^0_{Arr} \
\end{array} \right) \\[6pt]
&= \left( \begin{array}{c}
cos φ_{GL} \cdot x^0_{Arr} + sin φ_{GL} \cdot z^0_{Arr}\\
– sin φ_{GL} \cdot x^0_{Arr} + cos φ_{GL} \cdot z^0_{Arr}\
\end{array} \right) ・・・(26)
\end{align} \)
となる。
さて、ホイールベース \( wb \) はG/L方向のアクスル軸間の長さとなるため、\( x \)座標同士を引けばよいだけ。
よって、
\( \begin{align}
wb &= x_{Arr} – x_{Aft} =(cos φ_{GL} \cdot x^0_{Arr} + sin φ_{GL} \cdot z^0_{Arr}) \ – \ ( cos φ_{GL} \cdot x^0_{Aft} + sin φ_{GL} \cdot z^0_{Aft}) \\[6pt]
&= cos φ_{GL} \cdot (x^0_{Arr}- x^0_{Aft}) + sin φ_{GL} \cdot ( z^0_{Arr}-z^0_{Aft}) ・・・\small{(27)}
\end{align} \)
にて、G/L基準のホイールベースが算出できる。
G/L傾き \( φ_{GL}\) の算出の時に使った(20)式内 の \(a_x= x^0_{Arr} – x^0_{Aft} , a_z= z^0_{Arr} – z^0_{Aft} \) を再利用し、あわせて \( cos α = \dfrac{a_x}{\sqrt{a_x^2+a_z^2}} \) , \( sin α = \dfrac{a_z}{\sqrt{a_x^2+a_z^2}} \) も使えば
\( \begin{align}
wb &= {\sqrt{a_x^2+a_z^2}} \ (cos α \cdot cos φ_{GL} \ + \ sin α \cdot sin φ_{GL}) \\[6pt]
&= {\sqrt{a_x^2+a_z^2}} \ cos (α – φ_{GL}) ・・・\small{(28)}
\end{align} \)
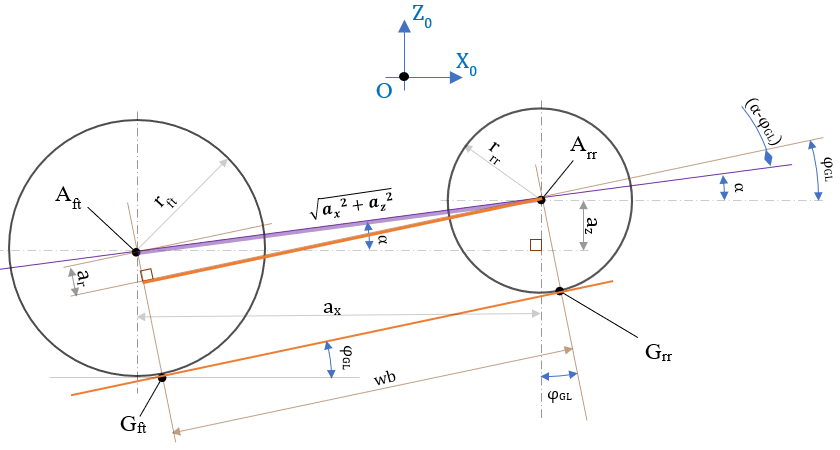
(27)式で十分だが、(21)式と同じ ( \(α – φ_{GL} ) \) が使えるので、こっちの方が普通かも。。
(面倒な計算せずとも上図を描けば、(28)式に直接たどりつける。。。)
G/L基準のトレール
つづいて、\( \small{O-X_1Z_1} \) において、\( \small{H/P} \) 軸 (ステアリング軸) を延長し\( \small{G/L} \) と交わる点を点 \(G_{tr} \) (= \( \left( \begin{array}{c}
x_{Gtr} \\
z_{GL} \
\end{array} \right) \) ) として、\( \small{O-X_1Z_1} \)におけるトレール長 \(tr\) (\(=|\overrightarrow{G_{tr}G_{ft}}|\)) (G/L基準) を求める。
原点\(O \)と(25)式の Frアクスル軸 \(A_{ft} \) を使えば、\( \overrightarrow{G_{tr}G_{ft}}\) は、
\( \begin{align}
\overrightarrow{G_{tr}G_{ft}} &= \overrightarrow{OG_{ft}}- \overrightarrow{OG_{tr}} \\[6pt]
&= (\overrightarrow{OA_{ft}} + \overrightarrow{A_{ft}G_{ft}}) \ – \ \overrightarrow{OG_{tr}} ・・・\small{(29)} \\[6pt]
\end{align} \)
である。
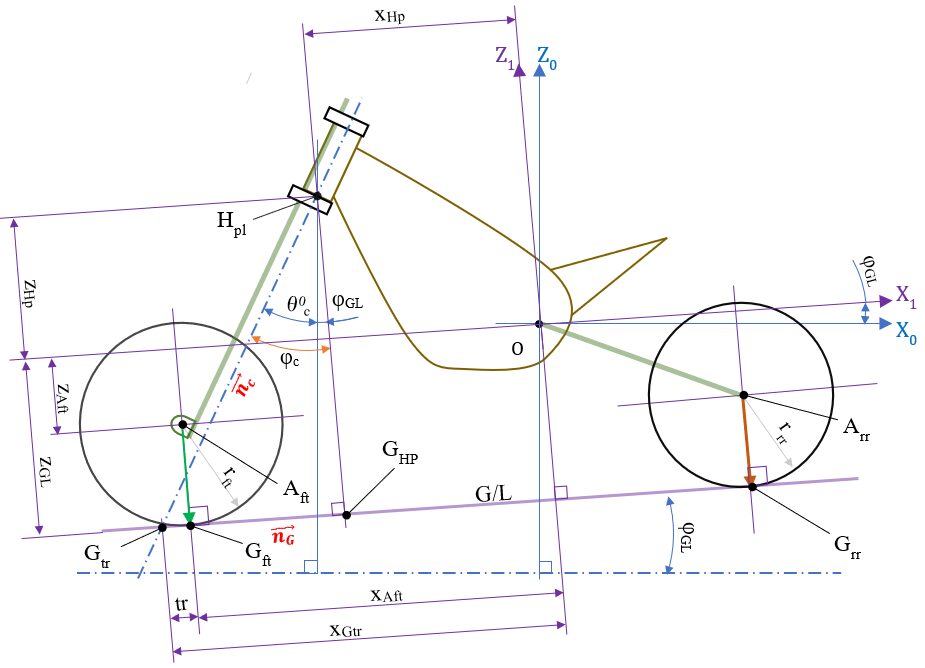
この(29) 式内で唯一未知の \( \overrightarrow{OG_{tr}} \) から求める。
\( \small{O-X_1Z_1} \) におけるH/P下端点 \( H_{pl} \) \( (= \left( \begin{array}{c}
x_{HP} \\
z_{HP} \
\end{array} \right) )\) のG/Lへの投影点を \( G_{HP} \) \( (= \left( \begin{array}{c}
x_{HP} \\
z_{GL} \
\end{array} \right) )\) と設定すれば、
\( \overrightarrow{OG_{tr}} = \overrightarrow{OG_{HP}} + \overrightarrow{G_{HP}G_{tr}} \) ・・・(30)
ここで、\( ⊿H_{pl}G_{tr}G_{HP} \)(図⑧) に着目し、\( \small{O-X_1Z_1} \) 上のG/L方向の単位ベクトル \( \overrightarrow{n_{G}} \) = \( \left( \begin{array}{c}
1 \\
0 \
\end{array} \right) \) 、キャスター角\(φ_c \ ( φ_c = θ^0_{c}+φ_{GL}) \) とすれば、(30)式内の \( \overrightarrow{G_{HP}G_{tr}} \) は、
\( \overrightarrow{G_{HP}G_{tr}} =|\overrightarrow{G_{HP}H_{pl}} |\cdot tan |{φ_c } |\cdot (- \overrightarrow{n_{G}}) \) ・・・(31)
である事から、(31)式 を (30)式 に入れ込めば、\( \overrightarrow{OG_{tr}} \) は
\( \begin{align}
\overrightarrow{OG_{tr}} &= \overrightarrow{OG_{HP}} + \overrightarrow{G_{HP}G_{tr}} \\[6pt]
&= \overrightarrow{OG_{HP}} \ – \ |\overrightarrow{G_{HP}H_{pl}} |\cdot tan |{φ_c }| \cdot \overrightarrow{n_{G}} ・・・\small{(32)}
\end{align} \)
求めたい\( \overrightarrow{G_{tr}G_{ft}}\)は、(29)式に(32)式を代入して
\( \begin{align}
\overrightarrow{G_{tr}G_{ft}}&= (\overrightarrow{OA_{ft}} + \overrightarrow{A_{ft}G_{ft}}) \ – \ \overrightarrow{OG_{tr}} \\[6pt]
&= ( \overrightarrow{OA_{ft}} + \overrightarrow{A_{ft}G_{ft}} ) \ – \ (\overrightarrow{OG_{HP}} \ – \ |\overrightarrow{G_{HP}H_{pl}} |\cdot tan |{φ_c }| \cdot \overrightarrow{n_{G}} ) \\[6pt]
&= \overrightarrow{OA_{ft}} + \overrightarrow{A_{ft}G_{ft}} \ – \ \overrightarrow{OG_{HP}} \ + \ |\overrightarrow{G_{HP}H_{pl}} |\cdot tan |{φ_c }| \cdot \overrightarrow{n_{G}}
\end{align} \)
となる。これに、\( |\overrightarrow{G_{HP}H_{pl}}|= z_{Hp} \ – \ (z_{Aft}-r_{ft}) 、(z_{GL}= z_{Aft}-r_{ft}) \) を踏まえ、成分値をいれれば、
\( \begin{align}
\overrightarrow{G_{tr}G_{ft}} &= \left( \begin{array}{c}
x_{Aft} \\
z_{Aft} \
\end{array} \right) + \left( \begin{array}{c}
0 \\
-r_{ft} \
\end{array} \right) \ – \ \left( \begin{array}{c}
x_{HP} \\
z_{GL} \
\end{array} \right) \ + ( \ z_{Hp} \ – \ (z_{Aft}-r_{ft})) \cdot tan | {φ_c }| \left( \begin{array}{c}
1 \\
0 \
\end{array} \right) \\[6pt]
& = \left( \begin{array}{c}
\ x_{Aft} \ – \ x_{HP} \ + \ (z_{Hp} \ -(z_{Aft} \ – \ r_{ft})) \cdot tan |{φ_c }|\\
0 \
\end{array} \right)
\end{align} \)
となる。トレール長 \(tr =|\overrightarrow{G_{ft}G_{tr}}|\) は、\(x \) 成分そのままで
\(tr =| ( x_{Aft} \ – \ x_{HP} \ + (\ z_{Hp} – z_{Aft} + r_{ft}) \cdot tan |{φ_c }|) | \) ・・・(34)
で求まる。
あとは \( \small{O_0-X_1Z_1} \) における成分値を取り込めばよいだけ。(23)式より
\( \left( \begin{array}{c}
x _{Aft}\\
z_{Aft} \
\end{array} \right) \) = \( \left( \begin{array}{c}
cos φ_{GL} \cdot x^0_{Aft} + sin φ_{GL} \cdot z^0_{Aft}\\
– sin φ_{GL} \cdot x^0_{Aft}+ cos φ_{GL} \cdot z^0_{Aft}\
\end{array} \right) \) ・・・(35)
\( \left( \begin{array}{c}
x _{HP}\\
z_{HP} \
\end{array} \right) \) = \( \left( \begin{array}{c}
cos φ_{GL} \cdot x^0_{HP} + sin φ_{GL} \cdot z^0_{HP}\\
– sin φ_{GL} \cdot x^0_{HP}+ cos φ_{GL} \cdot z^0_{HP}\
\end{array} \right) \) ・・・(36)
を使って、(34)式に代入すれば
\(\begin{align}
tr = & |(cos φ_{GL} \cdot x^0_{Aft} + sin φ_{GL} \cdot z^0_{Aft}) \\[6pt]
& \ – \ (cos φ_{GL} \cdot x^0_{HP} + sin φ_{GL} \cdot z^0_{HP}) \\[6pt]
& \ – \ (sin φ_{GL} \cdot x^0_{HP}\ – \ cos φ_{GL} \cdot z^0_{HP}) \cdot tan |({θ_{0c}+φ_{GL}}) | \\[6pt]
&+( sin φ_{GL} \cdot x^0_{Aft}\ – \ cos φ_{GL} \cdot z^0_{Aft}) \cdot tan |({θ_{0c}+φ_{GL}}) | \\[6pt]
&+r_{ft} \cdot tan |({θ_{0c}+φ_{GL}})|| ・・・\small{(37)}
\end{align} \)
で、(37) 式内の値は全て既知(今までの設定、算出値)となるので、G/L基準でのトレール長の算出は完了。
G/L基準のその他座標値の位置
\( \small{O-X_0Z_0} \) 上のばね上の任意の点(クランク位置、カウンター位置等々)の \( \small{O-X_1Z_1} \) への変換は、(23)式を使うだけなので割愛。
で、主な計算は完了と。。。
追記
追加計算:フロントアクスル位置ちょっと細かい版 (Step1 補足)
フロントアクスル軸( \( \small{\overrightarrow{OA_{ft}}}\) )については、変更できる諸元値がそこそこあるので(サス長変えたり、オフセット変えたり、サスの突き出し量を変えたり等々)、ついでに式に組み込んでおこうと。
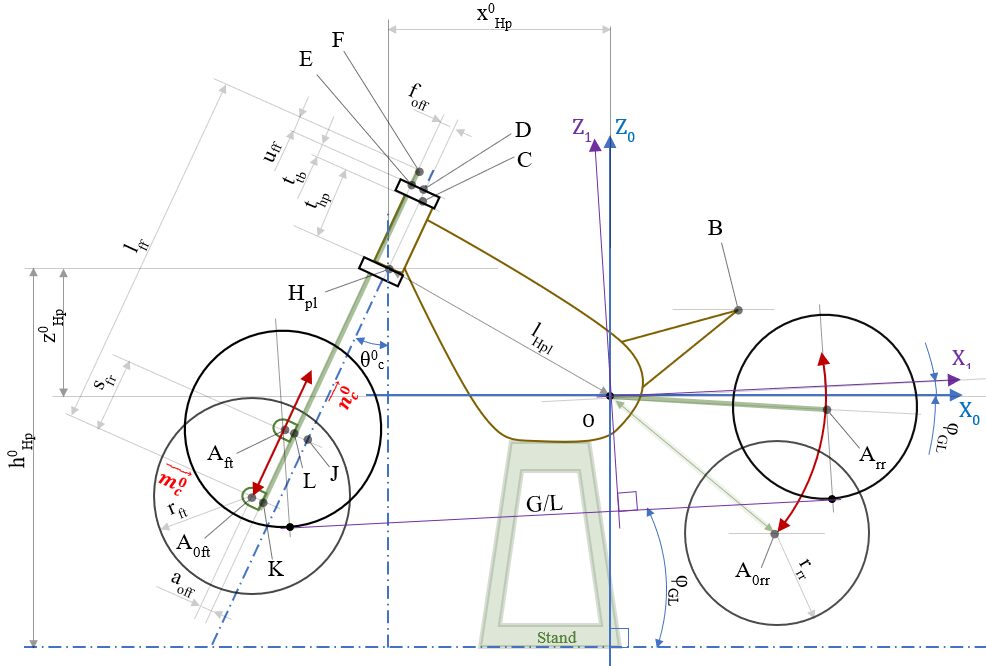
同様に点をなぞっていくだけで、単純なベクトルの足し算はStep.1と変わらない。
\(\overrightarrow{OA_{ft}} = \overrightarrow{OH_{pl}} +\overrightarrow{H_{pl}C}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}+\overrightarrow{FK}+\overrightarrow{KA_{0ft}}+\overrightarrow{A_{0ft}A_{ft}}\) ・・・(38)
この(38)式に、Step1と同様にキャスター角方向の方向ベクトル \( \overrightarrow{n^0_{c}} \) ( \( \vert \overrightarrow{n^0_{c}} \vert \) = 1) それに直交するベクトル \( \overrightarrow{m^0_{c}} \) ( \( \vert \overrightarrow{m^0_{c}} \vert \) = 1) を使えば、フロントアクスル位置 \( \small{\overrightarrow{OA_{ft}}} \)は、
\( \begin{align}
\overrightarrow{OA_{ft}}
= & \overrightarrow{OH_{pl}} +t_{hp} \cdot (- \overrightarrow{n^0_{c}}) +t_{tb} \cdot (-\overrightarrow{n^0_{c}})+f_{off}\cdot \overrightarrow{m^0_{c}} \\
& + u_{ff} \cdot (- \overrightarrow{n^0_{c}}) +l_{ff} \cdot \overrightarrow{n^0_{c}}+a_{off} \cdot \overrightarrow{m^0_{c}} +s_{fr} \cdot (- \overrightarrow{n^0_{c}}) \\
= & \overrightarrow{OH_{pl}} -(t_{hp}+t_{tb}+ u_{ff}-l_{ff}+s_{fr})\cdot \overrightarrow{n^0_{c}} +(f_{off}+a_{off}) \cdot \overrightarrow{m^0_{c}} ・・・(39)\
\end{align} \)
あとはこれを座標に落とし込めばよい。
\( \small{O-X_0Z_0} \)上でのベクトル成分 \( \overrightarrow{OA_{ft}}
= \left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft}\
\end{array} \right) \) 、 \( \overrightarrow{OH_{pl}}
= \left( \begin{array}{c}
x^0_{Hp} \\
z^0_{Hp} \
\end{array} \right) \) を使い、
また、Step1から \( \overrightarrow{n^0_{c}} \)= \(- \left( \begin{array}{c}
sin \theta^0_{c} \\
cos \theta^0_{c} \
\end{array} \right) \) 、\( \overrightarrow{m^0_{c}} \) = \( \left( \begin{array}{c}
-cos \theta^0_{c} \\
sin \theta^0_{c} \
\end{array} \right) \) を使えば、(39)式は、
\( \begin{align}
\left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft}\
\end{array} \right) = & \left( \begin{array}{c}
x^0_{Hp} \\
z^0_{Hp} \
\end{array} \right) + (t_{hp}+t_{tb}+ u_{ff}-l_{ff}+s_{fr})\cdot \left( \begin{array}{c}
sin \theta^0_{c} \\
cos \theta^0_{c} \
\end{array} \right) +(f_{off}+a_{off}) \cdot \left( \begin{array}{c}
-cos \theta^0_{c} \\
sin \theta^0_{c} \
\end{array} \right) \\[8pt]
= & \left( \begin{array}{c}
x^0_{Hp}+ (t_{hp}+t_{tb}+ u_{ff}-l_{ff}+s_{fr}) \cdot sin \theta^0_{c}-(f_{off}+a_{off}) \cdot cos \theta^0_{c} \\
z^0_{Hp}+ (t_{hp}+t_{tb}+ u_{ff}-l_{ff}+s_{fr}) \cdot cos \theta^0_{c}+(f_{off}+a_{off}) \cdot sin \theta^0_{c} \
\end{array} \right) ・・・(40) \\
\end{align} \)
フロントサス廻りのセッティング変更で変えそうなパラメータは一通り入っているはず。
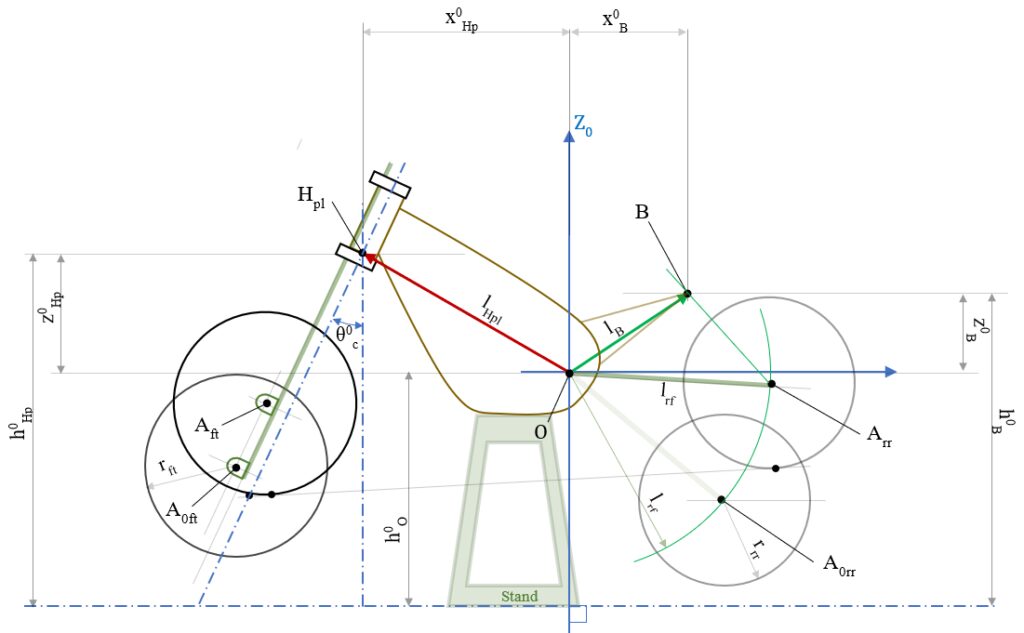
追加計算:” H/P座標、点Bの座標 ” (長さ&高さ計測からの算出)
ばね上を固定するH/P下端点 \(H_{pl} \)(Frサスストロークの基準点)と点 \(B\)(Rrサスストロークの基準点)の \( \small{O-X_0Z_0} \) 上における座標は、\( \overrightarrow{OH_{pl}}
= \left( \begin{array}{c}
x^0_{Hp} \\
z^0_{Hp} \
\end{array} \right) \)、\( \overrightarrow{OB}
= \left( \begin{array}{c}
x^0_{B} \\
z^0_{B} \
\end{array} \right) \) で設定しているが、少し追加。
というのも、直接測定のできる
- 点\(O\)-点\(H_{pl}\) 間の長さ : \(l_{Hpl}\)
- 点\(O\)-点\(B \)長さ : \(l_{B}\)
と 計測しやすい鉛直方向の方向の 各点の高さ
- \(h^0_{Hp}\)、\(h^0_{O}\)、\(h^0_{B}\)
を使っての座標算出の覚書。単純に三平方の定理と引き算を使うだけ
(車両モデルの座標定義から)、\( \small{O-X_0Z_0} \)に固定した車両モデルの H/P位置は \(x<0 \) である事を踏まえれば、それぞれの座標値は、
\( \left( \begin{array}{c}
x^0_{Hp} \\
z^0_{Hp} \
\end{array} \right) = \left( \begin{array}{c}
– \sqrt {{l_{HPl}}^2-(h^0_{Hp}-h^0_{O})^2 }\\
h^0_{Hp}-h^0_{O} \
\end{array} \right) \) ・・・(41)
\( \left( \begin{array}{c}
x^0_{B} \\
z^0_{B} \
\end{array} \right) = \left( \begin{array}{c}
\sqrt {{l_B}^2-(h^0_{B}-h^0_{O})^2 }\\
h^0_{B}-h^0_{O} \
\end{array} \right) \) ・・・(42)
補正計算:測定点の車両幅方向の補正
モデルはXZ平面上での二次元としたため、車両幅方向の測定点ずれ用の補正の覚書。実測定長さは以下で補正。
車両の幅方向のずれを \(l_{adj} \)、測定実長を \(l_{act} \)、計算に使う値を \(l_{xx} \) とすれば
\(l_{xx}= \sqrt{{l_{act}}^2- {l_{adj}}^2}) \) ・・・(43)
で補正
Note: 車両幅方向の測定点ずれとは、例えば、B点基準のリアストローク長 \(l_{rs} \)への補正。
下の図でいえば \(l_{xx} \) が \(l_{rs} \)になり、実測した\(l_{act} \)を車両幅方向の測定点ずれ \(l_{adj} \) にて補正し、\(l_{rs} \)として計算に使用。

実測時に計測点が車両幅一致する箇所で計測可能な場合は少ないかと思うので、補正を忘れぬようにと覚書
追加計算:キャスター角の算出 (長さ&高さ計測からの算出)
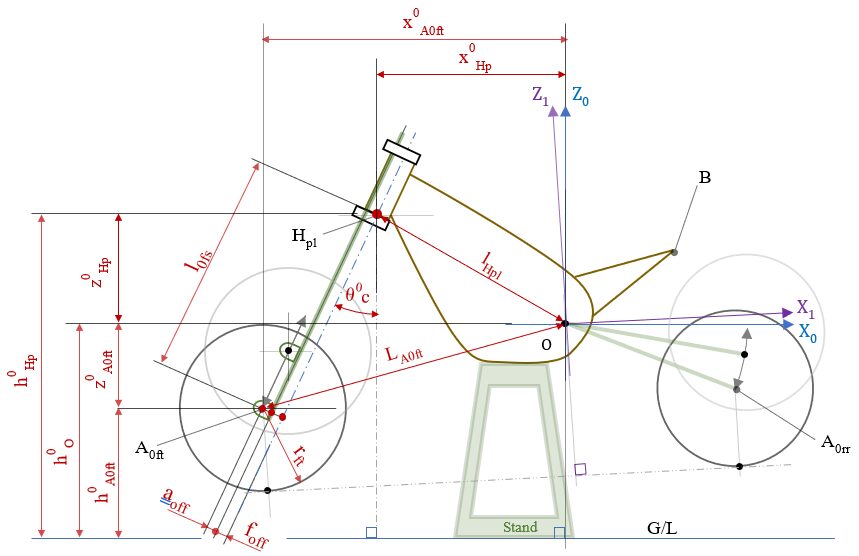
計測長測定のみからキャスター角を算出。(41)式の \( \small{H_{pl}} \) 座標、(5)式の \( \small{A_{0ft}} \) 座標につかった計測長から算出する
\( \left( \begin{array}{c}
x^0_{Hp} \\
z^0_{Hp} \
\end{array} \right) = \left( \begin{array}{c}
– \sqrt {{l_{HPl}}^2-(h^0_{Hp}-h^0_{O})^2 }\\
h^0_{Hp}-h^0_{O} \
\end{array} \right) \) ・・・(41)
を(5)式に使えば、Frアクスル座標は、
\( \begin{align}
\left( \begin{array}{c}
x^0_{Aft} \\
z^0_{Aft} \
\end{array} \right)
=& \left( \begin{array}{c}
x^ 0_{Hp}-l_{0fs} \cdot sin θ^0_{c} -(f_{off}+a_{off}) \cdot cosθ^0_{c}\\
z^0_{Hp}-l_{0fs} \cdot cos θ^0_{c}+(f_{off}+a_{off}) \cdot sin θ^0_{c}\
\end{array} \right) \\[6pt]
= & \left( \begin{array}{c}
– \sqrt {{l_{HPl}}^2-(h^0_{Hp}-h^0_{O})^2 }-l_{0fs} \cdot sin θ^0_{c} -(f_{off}+a_{off}) \cdot cos \theta^0_{c}\\
h^0_{Hp}-h^0_{O}-l_{0fs} \cdot cos θ^0_{c}+(f_{off}+a_{off}) \cdot sin θ^0_{c}\
\end{array} \right)・・・(45)
\end{align} \)
また、 \( \small{A_{0ft}} \) 座標は Frアクスル高 \( \small{h^0_{A0ft}} \) を使えば、
(Note : キャスター角の算出では使わないが、原点 \( \small{O} \) ~ Frアクスル \( \small{A_{0ft}} \) 間の距離は \( \small{l_{A0ft}} \) で記載)
\( \left( \begin{array}{c}
x^0_{A0ft} \\
z^0_{A0ft} \
\end{array} \right) = \left( \begin{array}{c}
– \sqrt {{l_{A0ft}}^2-(h^0_{A0ft}-h^0_{O})^2 }\\
h^0_{A0ft}-h^0_{O} \
\end{array} \right) ・・・(46) \)
(45)式 = (46)式 からキャスター角 \( θ^0_{c} \) を算出すればよい。\( z^0_{A0ft} \) 座標を抜き出して、
\( h^0_{Hp} – \cancel{h^0_{O}} – l_{0fs} \cdot cos θ^0_{c} + (f_{off}+a_{off}) \cdot sin θ^0_{c} = h^0_{A0ft}-\cancel{h^0_{O}} \)
整理すれば
\( l_{0fs} \cdot cos θ^0_{c} – (f_{off}+a_{off}) \cdot sin θ^0_{c} = h^0_{Hp} – h^0_{A0ft} \) ・・・(47)
ここで、\( sin β = \dfrac{f_{off}+a_{off}}{\sqrt{l_{0fs}^2+(f_{off}+a_{off})^2}} \) , \( cos β = \dfrac{l_{0fs}}{\sqrt{l_{0fs}^2+(f_{off}+a_{off})^2}} \) にて角度βを設定すれば、
\( cos β \cdot cos θ^0_{c} -sin β \cdot sin θ^0_{c} = \dfrac{h^0_{Hp} \ – \ h^0_{A0ft}}{\sqrt{l_{0fs}^2+(f_{off}+a_{off})^2}} \) となる。よって、cos の加法定理を使えば
\( cos (β + θ^0_{c}) = \dfrac{h^0_{Hp} \ – \ h^0_{A0ft}}{\sqrt{l_{0fs}^2+(f_{off}+a_{off})^2}} \)
これから
\( θ^0_{c} = arccos( \dfrac{h^0_{Hp} \ – \ h^0_{A0ft}}{\sqrt{l_{0fs}^2+(f_{off}+a_{off})^2}}) \ – \ β \) ・・・(48) 。
これに上の cosβ の定義からβを逆算して入れ込めば、
\( θ^0_{c} = arccos( \dfrac{h^0_{Hp} \ – \ h^0_{A0ft}}{\sqrt{l_{0fs}^2+(f_{off}+a_{off})^2}}) \ – \ arccos( \dfrac{l_{0fs}}{\sqrt{l_{0fs}^2+(f_{off}+a_{off})^2}} ) \) ・・・(48-1)
にて、キャスター角の長さ計測からの算出が完了
注記:G/Lの接線について
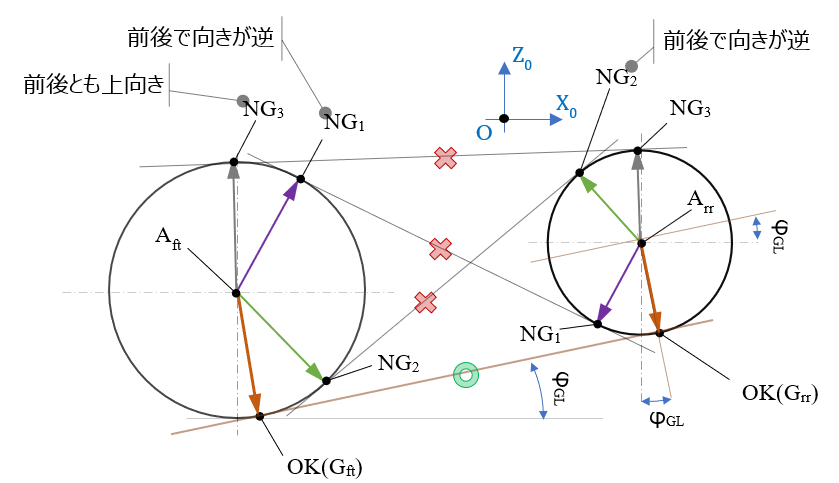
追加の覚書、上ではG/LはFrタイヤ&Rrタイヤの双方の接線となる事を使っているが、この(17)式の内積のみであれば、2つの円の接線は4通り成立するはず(下図)。
が、場合分けはちょっと面倒くさいので、ここでは
- (15)&(16)式で同じ方向のベクトルに設定、かつ
- \( φ_{GL} \) が \( – \dfrac{\pi}{2} ≦φ_{GL} ≦ \dfrac{\pi}{2} \) である事を利用して、(15)&(16)式の方向ベクトルを下向きに限定
( \(z \) 軸成分値は常に負 (\( – cos φ_{GL} ≦ 0\)) )
とすることにより、不要な3つの接線を対称から外し、必要なG/Lのみに限定させている(ちょっと強引)
さいごに
まぁ、今どき手計算でやる人はいないとは思うが、(実際はソフトで計算するにしろ)なんだ意外と手でも計算組めるじゃん、の実感があるのは悪くない、というのと、道具(ベクトル)の使い方を思い出したい時のための覚書。
力技でコツコツはじめて、後からしもた!と気づくのも幾つかあったが、まぁ、頭の体操という事で、、、
上の計算式を使った二輪車の車両諸元計算ツールも作った。こちらで、



