座標軸の定義
まずは、目の前の3次元の世界で考えていく
(こむずかしくいえば3次元のユークリッド空間)。
ちなみに、高次のユークリッド空間は定義を拡張して、次元を増やしていくだけなので、ここでは詳細割愛。
直交座標系の規則
さて、解析における座標設定時の一般的な規則としては、
(JISでもISOでも同じ定義)
直行系
座標軸の各軸は全て互いに直行 (各軸は互いに影響しない)
右手系
三次元における3つの軸は右手系 (右手の指で定義)
- x軸:親指
- y軸:人差し指
- z軸:中指
(指先の方向が正)
右ねじ系
回転方向の正負は、右ねじ系で定義
回転の正方向とは、各軸の正方向に右ねじを進める方向(時計回り)の回転方法が正
例えば
- z軸まわりの回転は、x軸->y軸方向の回転が正
- x軸まわりの回転は、y軸->z軸方向の回転が正
- y軸まわりの回転は、z軸->x軸方向の回転が正
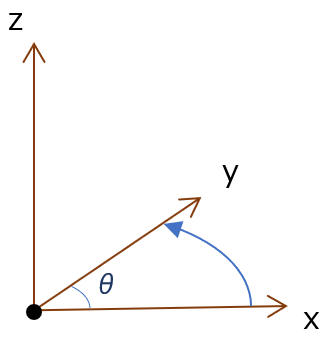
複数の座標系
空間上の座標系は一つである必要はない。
グローバル座標(絶対空間の定義)、ローカル座標(その空間内を移動する物体に固定された座標)と、複数設定可能。
座標表示
n次元空間上の任意の点の各軸の成分表示として、
- 列方向:\( \left ( \begin{array}{c}
a_{0}\\
a_{1} \\
\vdots\\
a_{n}
\end{array} \right ) \)
もしくは、
- 行方向:\( \left ( a_{0},~a_{1},~\ldots,~a_{n} \right ) \)
で表し、これは列ベクトル、行ベクトルと同じ表記。
例えば、3次元空間上の任意の点のxyz座標は、\( \left ( \begin{array}{c}
x\\
y \\
z
\end{array} \right ) \) もしくは \( \left (x,~y,~z \right ) \) となる。
極座標表示:ピタゴラスの定理から三角関数、極座標表示への展開
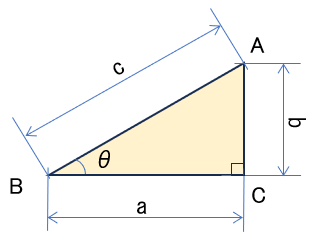
ピタゴラスの定理(三平方の定理)
三角関数の導入前にピタゴラスの定理から、
三角関数と円
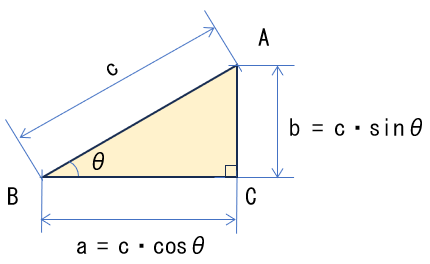
さて、前述のピタゴラスの定理で使用した直角三角形ABC の辺BAと辺BCのなす角をθとして、三角関数の定義を行う。
この三角関数の定義をつかえば、直角三角形の各辺の長さ a と b は
\(a = c\cdot cosθ \) , \( b =c\cdot sinθ \) ・・・②
で表され、
これをピタゴラスの定理(①式)に代入すれば、
\( (c\cdot cosθ)^2+ (c \cdot sinθ)^2=c^2 \)
両辺からcが消して
cosθ と sinθ の基本的な関係式としてよく見るが、とどのつまりは三角関数を使ってピタゴラスの定理を表現しているだけ(言っている事は同じ)。
極座標
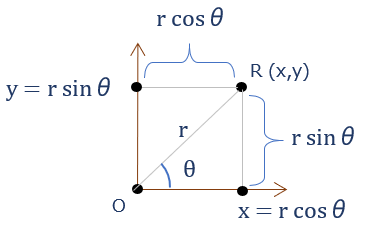
さて、x-y座標系上の任意の点R \( \left ( \begin{array}{c}
x\\
y \end{array} \right ) \) は、
- 原点Oと点Rの距離:r
- x軸とORのなす角:θ
を使えば、②式(三角関数の定義(右図も参照))から
この \( \left ( \begin{array}{c}
x\\
y
\end{array} \right ) \)を r とθ の2変数で表したものを極座標という。
r を一定にθのみを変えていく点の軌跡は、中心からの一定距離rを保った点の軌跡、つまり円。
これから円の公式は、極座標の成分(④式)を、①式のピタゴラスの定理に当てはめて
\(x^2+y^2= (r \cdot cosθ)^2+(r \cdot sinθ) ^2= r^2 ( cos^{2}θ+ sin^{2}θ) \)
③式 ( \( cos^2 θ+ sin^2θ=1 \)) より、\(x^2+y^2= r^2 \) <- 円の公式がでる
ちなみに、極座標表示 (r, θ) にて、θ を一定に r を変えていけば点の軌跡は”直線”を描き、r と θ を共に変えていけば”曲線”を描く。
追記
結局、ピタゴラスの定理も、sin2θ + cos2θ =1 の関係式も、円の方程式(x2 + y2 = r2)も、見方を変えてその特徴を別表現しているだけ。
ちなみに、極座標とわざわざ宣言して使用されているわけではなく、特に曲線/円を描く場合に、x成分、y成分表示として、式の中に普通に紛れ込んでいる。
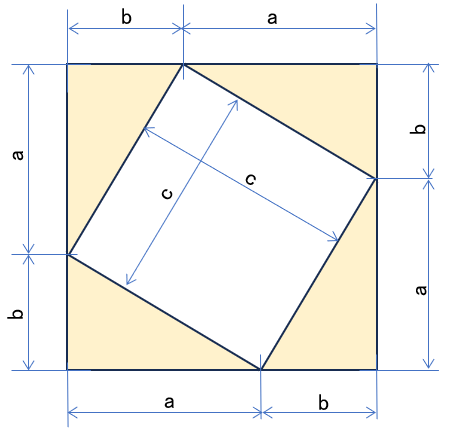
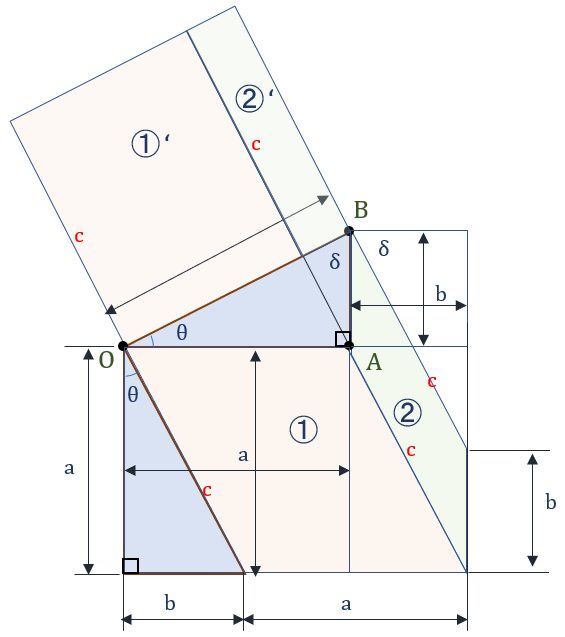
蛇足:ピタゴラスの定理の図解②
ピタゴラスの定理を(式を使わずに)面積のやり取りで証明するには、以下