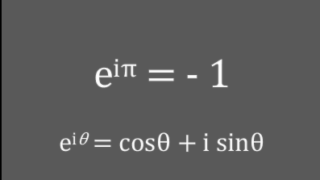オイラーの公式を導く
前回の記事は、オイラーの公式 :\( e^{i \theta}=cos \theta + i \cdot sin \theta \) ・・・① の見方と使い方の例について書いた。
今回はそのオイラーの公式の導き方。
右辺の ” \( e^{i \theta} \) ” と左辺の ” \( cos \theta + i \cdot sin \theta \) ” が等しい事の説明
オイラーの公式は、” ネイピア数 \( e \)の指数関数 と 三角関数 の等式化 ” 。
それぞれの関数をマクローリン展開(級数展開)し、微分時に各関数がもつ性質を上手に使い、右辺の \( e^{i \theta} \) と 左辺の \( cos \theta + i \cdot sin \theta \) が等しい事を証明している。
本記事はこの部分を詳細に。。。
ちなみに、結論から言えば \( e^{i \theta} \)、\( cos \theta \) 、\( i \cdot sin \theta \) をそれぞれマクローリン展開すれば、
\( \begin{align}
e^{iθ} &= \dfrac{1}{0!}θ^{0} + \dfrac{i}{1!}θ^{1} + \dfrac{-1}{2!}θ^{2} + \dfrac{-i}{3!}θ^{3} + \dfrac{1}{4!}θ^{4} + \cdots ・・・②\\
cos θ &= \dfrac{1}{0!}θ^{0} + \cancel{\dfrac{0}{1!}θ^{1}} + \dfrac{-1}{2!}θ^{2} + \cancel{\dfrac{0}{3!}θ^{3}} + \dfrac{1}{4!}θ^{4} + \cdots ・・・③ \\
i \cdot sin θ &= \cancel{\dfrac{0}{0!}θ^{0}} + \dfrac{i}{1!}θ^{1} + \cancel{\dfrac{0}{2!}θ^{2}} + \dfrac{-i}{3!}θ^{3} + \cancel{\dfrac{0}{4!}θ^{4}} + \cdots ・・・④ \\
\end{align} \)
② = ③ + ④、これを使って、 ” \( e^{i \theta} \) ” と ” \( cos \theta + i \cdot sin \theta \) ” が 等しい事を述べているに過ぎないが、この導入過程において、微分、指数関数、三角関数、ネイピア数、虚数の特徴を、これでもかというぐらいうまーく利用している。
それぞれが別世界で定義されたものとは思えない。とにかく、うまい。
(複雑なパズルがきれいに組み合わさった時のすっきり感さえある。)
この成立ちの背景を一通り記載。
eの指数関数 e^θ 、三角関数 cosθ 、sinθ 、虚数 i の 各性質
ネイピア数の指数関数 \( e^θ \) 、三角関数 \( cosθ \) 、\( sinθ \)、虚数 \( i \) の各性質について、今回のオイラーの公式の導入に必要なトコロだけざっくりと。まずは使われている各特徴から
ネイピア数 e の指数関数 e^θ の微分の性質
まず、ネイピア数 を使った指数関数 \( e^θ \) 。
これは微分において、何度微分しても \( e^θ \) のままという特別な特徴を持っている。つまり形を変えない。
\( \dfrac{d}{dθ}(e^θ) = e^θ \)・・・⑤
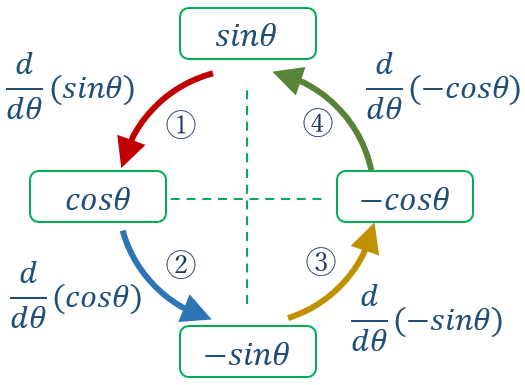
三角関数 cosθ 、sinθ の微分の性質
続いて、三角関数。
例えば、\( sinθ \)の微分を繰り返すと
\( sinθ \) -> \( cosθ \) -> \( – sinθ \) -> \( – cosθ \) -> \( sinθ \)
こちらは、微分を4回繰り返すと元に戻る。
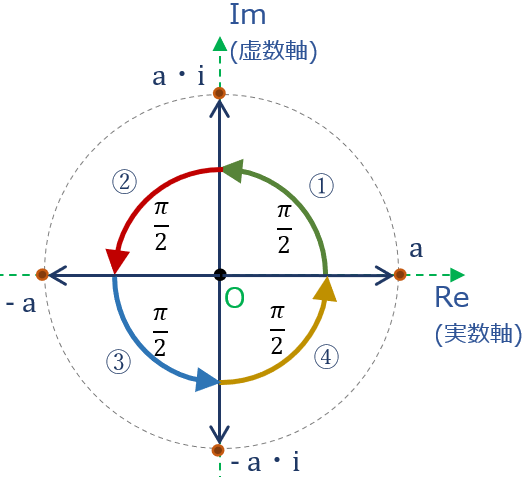
虚数 i のかけ算
虚数単位 \( i \) は、\( i = \sqrt{-1} \) つまり
\( i ^2 = -1 \) ・・・⑥
例えば、実数 \( a \) に繰り返し \( i \) をかけてみれば、
\( a \) -> \( a \cdot i \) -> \( -a \) (\( =a \cdot i ^2 \) ) -> \( -a \cdot i \) -> \( a \) (\( = -a \cdot i ^2 \) )
つまり、虚数 \( i \) を4回かけると元の実数に戻る。
くるくる回る虚数の振る舞いについては、こちらにも少し。
テイラーの定理 から マクローリン展開まで
これらの各性質を踏まえ、オイラーの公式を導くのに必要な道具である級数展開のうち、テイラーの定理からはじめてマクローリン展開まで説明。
級数展開とは
級数展開というと面倒な感じがするが、要は
- ある数(関数)を数列の和(関数の和)に置き換える事
-> 左辺の関数と別関数の無限級数の和である右辺が ”=” で結ぶ事ができるトコロが肝
実際、下のテイラー展開とかマグローリン展開とか、”いつ使うんだよ”、みたいな感じだが、このある関数を無限級数の和で置換できるという級数展開自体の考え方は、実生活でもいろいろなトコロで見る事ができる。
画像Formatのjpeg とかでデータ圧縮型に使われていたり、周波数解析で使うフーリエ変換も考え方としては同じ級数展開の考え方
(もちろん級数展開自体はそれぞれ異なるが、無限に飛ばすと剰余項が”0”に収束するから、元の関数が再現できるという考え方は同じ)
テイラーの定理
マクローリン展開は、テイラー展開の限定版。このテイラー展開は、テイラーの定理から導かれる。
といった訳で、まずはテイラーの定理から
これが何を言っているかというと、
この定理は、\( \displaystyle \sum_{k=0}^{n-1} \dfrac{f^{(k)}(a)}{k!}(x-a)^k \) を使って\( f(x) \)を級数展開(x=aを基点した微分を含む関数処理)した項の(n-1)個までの総和の最後のn個目として、その関数の和はf(x)と一致させる\( \dfrac{f^{(n)}(c)}{n!}(x-a)^n \) ”項”が存在すると述べている。
(最後の項では、aの代わりにc(a <c< x)を微分値に使う )。
ちなみに、この最後のつじつま合わせの項は、”剰余項”と呼ばれる。
(ちなみに、級数展開方法自体も様々なタイプがあり、剰余項にも様々なタイプがある)
さて、このテイラーの定理を、a=0で特化したのがマクローリンの定理。
テイラー展開からマクローリン展開
さて、\( n → ∞ \) とした時に、剰余項 \(R_n \) が \(R_n → 0 \) に収束すれば、\( f(x) \) は剰余項なく無限級数展開で置き換える事ができることになる。( 当然、\(R_n \) が0に収束せずに近似しきれない \( f(x) \) もある。)
ただ、\(R_n → 0 \)に収束する場合には、⑥式は
\( f(x) = \displaystyle \sum_{n=0}^{∞} \dfrac{f^{(n)}(a)}{n!}(x-a)^n \) ・・・⑧
となり、これがテイラー展開による \( f(x) \) の級数展開。
加えて、基点を \( a=0 \)とした
\( f(x) = \displaystyle \sum_{n=0}^{∞} \dfrac{f^{(n)}(0)}{n!}x^n \) ・・・⑨
これがマクローリン展開。
さて、指数関数 \(e^θ \) 、三角関数 \(sinθ \)、\(cosθ \) のラグランジェの剰余項 \(R_n \) は、\(n → ∞ \)の時に \(R_n → 0 \) に収束する。つまり、このマクローリン展開 を使って級数展開する事が可能。
(\(R_n → 0 \) は、ここでは既知として話を進める、証明は別途)。
さてここから、本題のオイラーの公式に。
オイラーの公式は、\(e^θ \) 、 \(sinθ \)、\(cosθ \) をマクローリン展開した級数の組合せで簡単に算出できる。
e^θ 、sinθ 、cosθ のマクローリン展開
\(e^θ \) 、\(sinθ \)、\(cosθ \) のマクローリン展開を求めるのに、まず関数 \(f(θ)\) のマグローリン展開
\( f(θ) = \displaystyle \sum_{n=0}^{∞} \dfrac{f^{(n)}(0)}{n!}θ^n \) ・・・⑧
の分子部分 \( f^{(n)}(0) \) を調べると、上述の各性質から
- \( f(θ) \) が \(e^θ \) であれば、1のまま
- \( f(θ) \) が \(sinθ \) であれば、\( 1 → 0 → -1 → 0 \) の循環
- \( f(θ) \) が \(cosθ \) であれば、\(0 → 1 → 0 → -1 \) の循環
となっている事がわかる。それぞれに虚数 \( i \) を組み合わせれば以下(下図)
(虚数を組み合わせてもこれらの関数において、4回繰り返すと元に戻るという事がポイント)
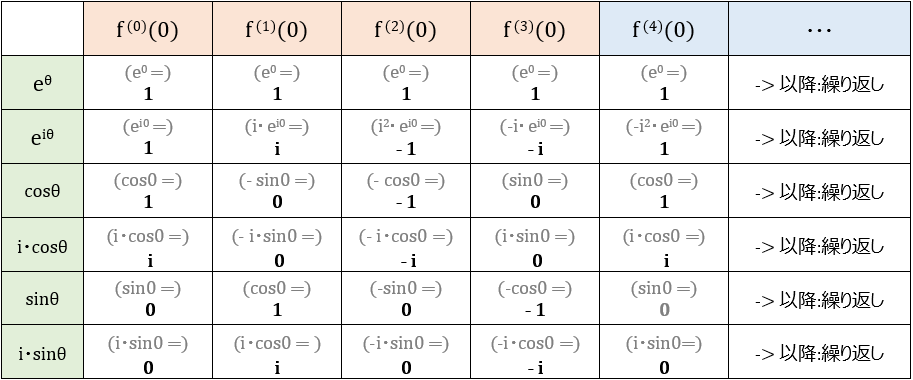
すべて、微分を4回繰り返す毎に元に戻る性質は共通している。これを使う。
上の表を参照にマクローリン展開の式に当てはめれば、\(e^θ \) 、 \(e^{iθ} \)、 \(sinθ \)、\(cosθ \) の無限級数が簡単に出来上がり、
\( \begin{align}
\color{gray}{e^{θ}} &= \color{gray}{\dfrac{1}{0!}θ^{0} + \dfrac{1}{1!}θ^{1} + \dfrac{1}{2!}θ^{2} + \dfrac{1}{3!}θ^{3} + \dfrac{1}{4!}θ^{4} + \cdots ・・・②’}\\
e^{iθ} &= \dfrac{1}{0!}θ^{0} + \dfrac{i}{1!}θ^{1} + \dfrac{-1}{2!}θ^{2} + \dfrac{-i}{3!}θ^{3} + \dfrac{1}{4!}θ^{4} + \cdots ・・・②\\
cos θ &= \dfrac{1}{0!}θ^{0} + \cancel{\dfrac{0}{1!}θ^{1}} + \dfrac{-1}{2!}θ^{2} + \cancel{\dfrac{0}{3!}θ^{3}} + \dfrac{1}{4!}θ^{4} + \cdots ・・・③ \\
\color{gray}{i \cdot cos θ} &= \color{gray}{\dfrac{i}{0!}θ^{0} + \cancel{\dfrac{0}{1!}θ^{1}} + \dfrac{-i}{2!}θ^{2} + \cancel{\dfrac{0}{3!}θ^{3}} + \dfrac{i}{4!}θ^{4} + \cdots ・・・③’} \\
\color{gray}{sin θ} &=\color{gray}{ \cancel{\dfrac{0}{0!}θ^{0}} + \dfrac{1}{1!}θ^{1} + \cancel{\dfrac{0}{2!}θ^{2}} + \dfrac{-1}{3!}θ^{3} + \cancel{\dfrac{0}{4!}θ^{4}} + \cdots ・・・④’} \\
i \cdot sin θ &= \cancel{\dfrac{0}{0!}θ^{0}} + \dfrac{i}{1!}θ^{1} + \cancel{\dfrac{0}{2!}θ^{2}} + \dfrac{-i}{3!}θ^{3} + \cancel{\dfrac{0}{4!}θ^{4}} + \cdots ・・・④ \\
\end{align} \)
オイラーの公式
さて、ここまで来たらオイラーの公式までたどり着くのは簡単。(パズルがココですっきりと組み合わさる)
単純に上から②③④式を引っ張り出せば、冒頭の ②=③+④ が成り立っている事がわかる
\( \begin{align}
e^{iθ} &= \dfrac{1}{0!}θ^{0} + \dfrac{i}{1!}θ^{1} + \dfrac{-1}{2!}θ^{2} + \dfrac{-i}{3!}θ^{3} + \dfrac{1}{4!}θ^{4} + \cdots ・・・②\\
cos θ &= \dfrac{1}{0!}θ^{0} + \cancel{\dfrac{0}{1!}θ^{1}} + \dfrac{-1}{2!}θ^{2} + \cancel{\dfrac{0}{3!}θ^{3}} + \dfrac{1}{4!}θ^{4} + \cdots ・・・③ \\
i \cdot sin θ &= \cancel{\dfrac{0}{0!}θ^{0}} + \dfrac{i}{1!}θ^{1} + \cancel{\dfrac{0}{2!}θ^{2}} + \dfrac{-i}{3!}θ^{3} + \cancel{\dfrac{0}{4!}θ^{4}} + \cdots ・・・④ \\
\end{align} \)
で、、
\( e^{i \theta}=cos \theta + i \cdot sin \theta \) ・・・①
のオイラーの公式が導かれる。
追記
前回の記事にて
と書いたが、導入に級数展開をも使い、過去の蓄積された数学の各世界のそれぞれのルールを崩すことなく統一しているのが、オイラーの公式。
ここが”美しい”と言われる所以。
上のテイラー展開については、こちらの本がおススメ(実数・虚数についてのおススメ本と同じ)
オイラーの公式については、この本もおすすめ。。
流し読みとまではいかないが、読み物としても面白い。