はじめに
機械設計であれば、誰もが使用するねじ。。
ただ、ねじは実際に”設計”をしているというより、”勘”、”経験”、 ”踏襲(模倣)” による ”選択” をしているのが実情。
もともと ”規格品を使用する事” による ”選択” を前提とした部品であり、めったにそれ自身の ”設計” を行う事はほとんどないねじであるが、勘等による選択だけでは、たまに困る時もある。
例えば、使用中に”緩み”が発生する場合とかとか。
少し知識加えれば、より根拠のある設計(選択)が可能になる。
ちなみにおすすめの本はこの二冊
”ねじ締結の原理と設計”は、ねじの理論的背景が一通り網羅されている(式の中の定数を数字に置き換えたりで、もうちょっと素直に書いてくれれば。。。とも思うが、情報量が豊富。持っていると安心できる)
”ねじ締結概論” は、より実務的な視点から書いてある(こちらの方がよりストレート)。
この二冊があれば締結に関する調べ事はだいたい事足りる(かと)。
ねじ(ボルト)の各部の名称
ねじの各部の名称
まずは、ねじの各部の名称。ねじにもいろいろ種類があるが、まずは六角のフランジボルトを例にとる。
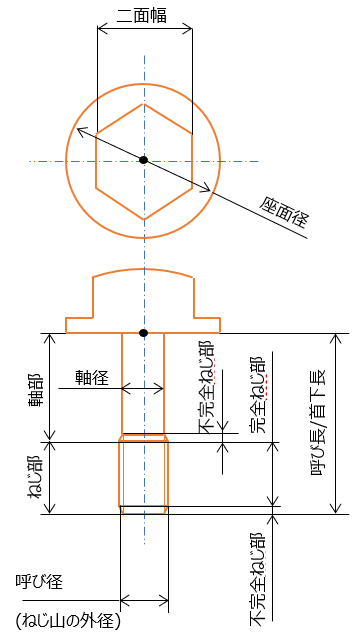
ねじの呼び方
呼び径はおねじの”外径”。 ボルトナット問わず、一般的にこれがねじのサイズを示す。
ビスを除き、ボルト/ナットでは、メートルねじを意味する”M” と組み合わせてにて、M8のボルト、M10のナット等々で呼ばれる。さて、
平目ねじ(例:M10)
平目ねじは”M” に”呼び径”をつける (たとえば、呼び径10mmの平目ねじであれば、M10)。
各呼び径に対応するピッチは一種類のみのため記載不要(JIS)。
細目ねじ(例:M10x1.25)
平目ねじより小さいピッチの細目ねじの場合。
細目ねじの場合は、ピッチを追加して、 平目ねじの”M+呼び径” に、x”ピッチ”を追加(たとえば、呼び径10mmの細目ねじであれば、M10X1.25)。
その他:呼び長(首下長)も合わせた表示の場合
”M”+ ”呼び径” + ”x 呼び長(首下長)” を組みあわせた表記もよく目にする。たとえば、M6X18 -> 呼び径 6mm+呼び長 18mmの平目ねじ
(”xピッチ”と”x首下長”の表記が同じになるが、その表記されている長さとその含む意味が明らかに違うので、区別に困る事はあまりない)
まとめれば
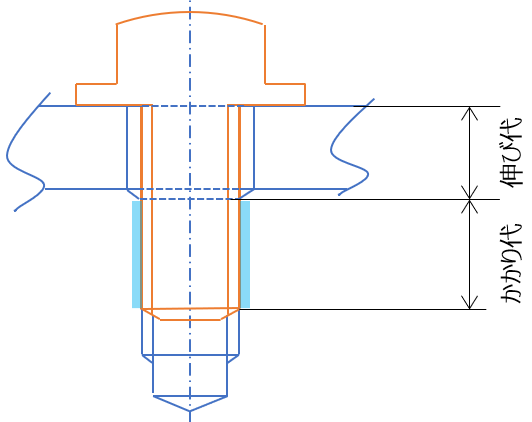
<かかり代と伸び代>
ちなみに、おねじとめねじの勘合する長さをねじのかかり代(勘合長)、ねじの首下からかかり代までの軸の長さをねじの伸び代とよぶ。
続いて、”ねじ諸元の名称と定義”について
ねじ諸元の名称と定義
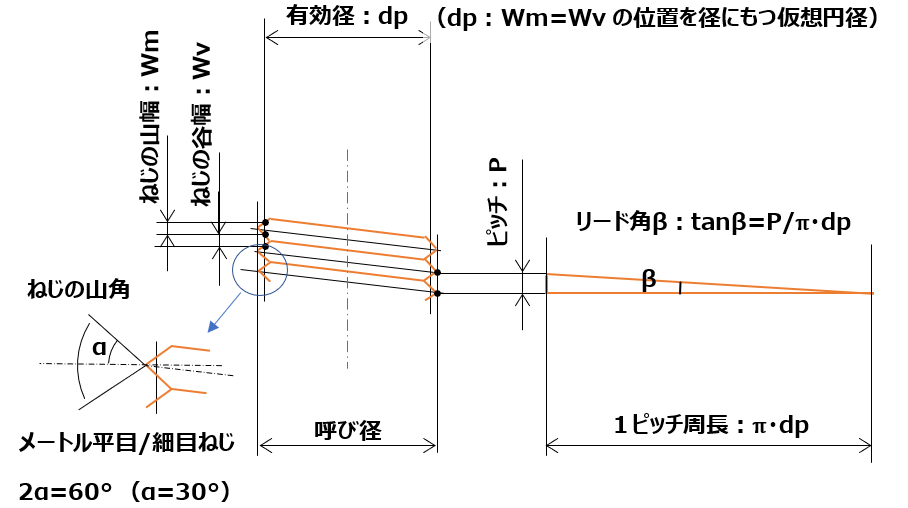
ついでに、ねじ部諸元の名称については以下。(小文字:おねじ、大文字:めねじ)
- ねじの呼び径:d (or D)
-> おねじの山径(めねじの谷径) - ねじの有効径:d2(or D2)
-> ねじの山径/谷径の間にて、山幅=谷幅の位置を径とする仮想円径 (dp) - おねじ谷底径(めねじ山径):d1 (or D1)
- ピッチ:P
-> 隣り合うねじ山同士の間隔 - リード角:β
-> ねじが一周まわる間に1ピッチ分上がる角度(一条ねじの場合:n条ねじの場合はn倍) - ねじ山半角:α
-> ねじ山頂点の角度/2(平目/細目ねじでは2α= 60°(π/6))
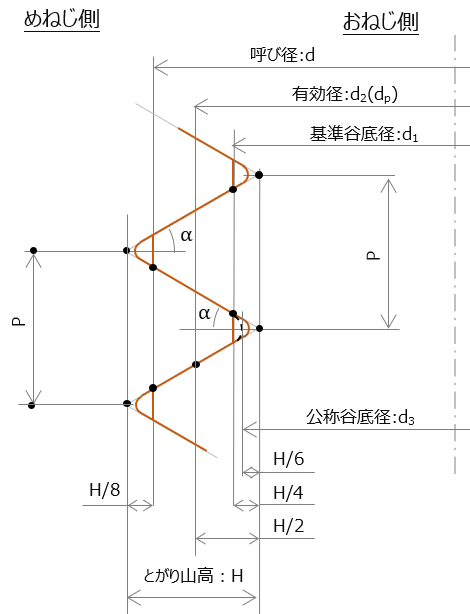
(ざっくり言えば、おねじ/めねじは正三角形の山の組合せ) - とがり山高さ:H
-> ねじ山を構成する正三角形の高さ
またとがり山高さは、\( H=\displaystyle \frac{P}{2\tan{\alpha}}\)
ねじの有効径は、
\(
\begin{align}
d_2(or \ D_2) &=d-2\cdot (\displaystyle \frac{H}{2}-\displaystyle \frac{H}{8}) \\[8pt]
&=d-\displaystyle \frac{3}{4}H \\[8pt]
&= d-\displaystyle \frac{3P}{8\tan{\alpha}}
\end{align}
\)
おねじ谷底径(めねじ山径)は、
\(
\begin{align}
d_1(or \ D_1)&=d-2\cdot(H-\displaystyle \frac{H}{8}-\displaystyle \frac{H}{4})\\[8pt]
&=d-\displaystyle \frac{5}{4}H\\[8pt]
&=d-\displaystyle \frac{5P}{8\tan{\alpha}}
\end{align} \)
を並目/細目ねじの基準山形として扱う。
Note:この先の軸力計算に用いるおねじの有効断面積Asには、谷底径のd1定義における切取り高さH/4 を(谷底面は円で接するとして)H/6で置き換えた径 d3を用いる。まずd3 は
\(
\begin{align}
d_3&= d-2\cdot(H-\displaystyle \frac{H}{8}-\displaystyle \frac{H}{6})\\[8pt]
&=d-\displaystyle \frac{17}{12}H\\[8pt]
&= d-\displaystyle \frac{17P}{24\tan{\alpha}}
\end{align} \)
であり、この谷底径d3 と おねじの有効径d2 の平均値ds がおねじの有効断面積Asの径である。ds は
\(
\begin{align}
d_s&=\displaystyle \frac{d_2+d_3}{2}\\[8pt]
&=d-2\cdot(H-\displaystyle \frac{H}{8}-\displaystyle \frac{H}{6})\\[8pt]
&=d-\displaystyle \frac{13}{12}H\\[8pt]
&=d-\displaystyle \frac{13P}{24\tan{\alpha}}
\end{align} \)
これを使い、おねじの有効断面積Asは
\(
\begin{align}
A_s &=\pi \cdot \displaystyle (\frac{d_s}{2})^2 \\[8pt]
&= \displaystyle \frac{\pi }{4}\cdot(d-\displaystyle \frac{13P}{24\tan{\alpha}} )^2
\end{align} \)
となる。
続いて、ざっくりと”ねじの締結の仕組み”と”締め付け線図”について
ねじの締結の仕組み(概要)
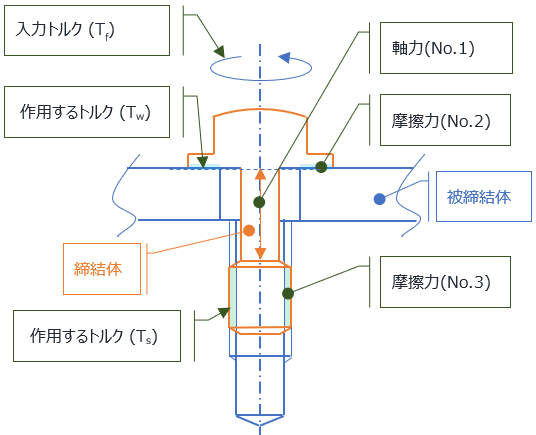
ねじによる締結とは、入力されるトルクを軸力に変換し(軸を伸ばして発生する力)、発生する軸力により被締結体を固定する事。
ボルトに入力されるトルクTf(T)は
- ねじ部に作用するトルク(a):Ts
- ボルト座面に作用するトルク(b):Tw
の二か所に作用し ( Tf = Ts + Tw)、
そのトルクは
- ボルトの軸部が伸びる事により発生する軸力(No.1)
- (1の発生により) ボルト座面に発生する摩擦力(No.2)
- (1の発生により) ボルトねじ面に発生する摩擦力(No.3)
の3つを発生させる。
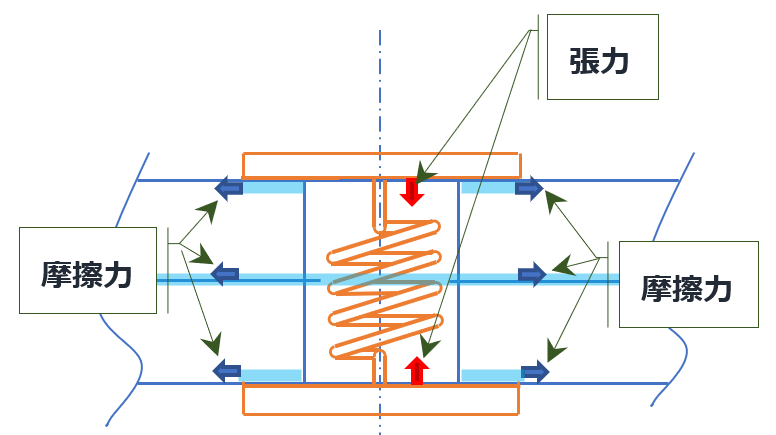
また、被締結体は
- 発生するNo.1の軸力
:(ねじの軸方向) - No.1の軸力により発生する摩擦力(締結体と被締結体間、もしくは被締結体同士)
:(ねじの軸直角方向)
により固定される。
このボルトの軸力発生による被締結体を固定する仕組みが”ねじによる締結”の基本。
締め付け線図
締め付け線図とは
ボルトが伸ばされ軸力が発生すれば、その軸力を受け止める被締結体側は圧縮され、軸力につりあう圧縮力が発生する。
この力の釣り合い状態を示したものが締め付け線図(前提:弾性域内での使用)。
締め付け線図の中身
締め付け線図は単純に、発生荷重を縦軸にして、伸び量(ボルト側)と縮み量(被締結体側)を一つのグラフにまとめたもの。
まとめる前に、まずはねじ側& 被締結体側にわけたグラフから。
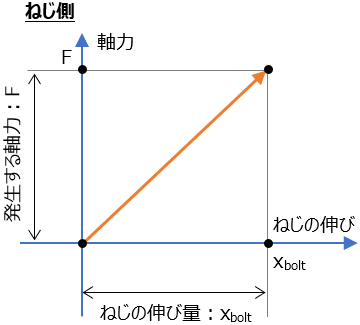
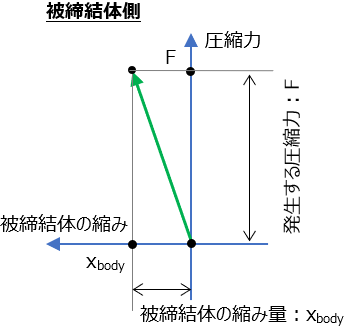
弾性域内で使用している限り、荷重と変位量(伸び量と 縮み量)は線形一次の形(バネでも有名なフックの法則に従う)になる。
- F = K・x
(F:力、K:定数、x:伸び)
これをねじ側、被締結側を別々に書けば以下(単純にフックの法則のグラフ化)
ねじ発生している軸力Fと被締結体側への圧縮による力はつり合っているため、Fの大きさは同じ値(縦軸)、このふたつを結合して
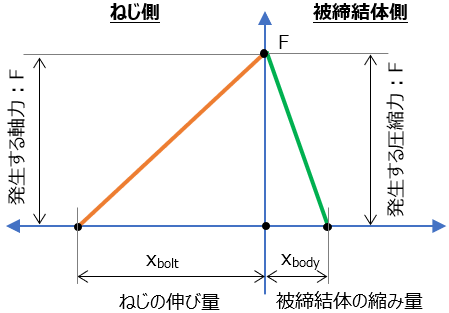
これが締め付け線図。
ボルト側のばね定数 Kboltについて
荷重の変位量をΔF、伸び/縮みの変位量をΔxとすれば
- ΔF=KΔx
詳細は割愛するが、このねじのバネ定数 Kboltは
- 伸び代部の仕様(断面積に比例し、長さ(伸び代)に反比例)できまる弾性
- ボルト/ナットの頭部の仕様できまる弾性
によって決まる。
伸び代部のバネ定数については、材料力学の教科書に書いてあるフックの法則から簡単に導くことができる(σ=Eε (σ:応力、E:縦弾性係数、ε:ひずみ:詳細は ”ねじ締結の原理と設計” ご参照)。
式だけ書けば、軸の断面積をA、伸び代をLとして
Kbolt =E・A / L
つまり軸径が大きい方が Kbolt は大きく、伸び代が長い方がKbolt は小さくなる。
-> 通常のばねのバネ定数と見方は同じ
(ばね径が大くなればバネ定数は増加、バネ長が長くなれば バネ定数減少)。
さて、設計時の注意点としては、ボルトナットの頭部はほぼ規格化されているが、伸び代部の設定はその締結箇所の設計依存。
つまり、同一ボルトを使用していても、締結箇所の設計次第で定数 Kboltは異なる(変える事ができる)。
->設定(設計)でソコソコ基本を押さえる必要あり。。。
ボルト頭部を含むボルト全体のバネ定数詳細は、 ”ねじの原理と設計” へ。
被締結体の圧縮側の定数 Kbody の詳細もあるのでここを読んでおけば、イメージはつかめる。
つまり、”ボルトの伸び”対”軸力”の関係(線形一次の関係)示す定数が、この Kbolt 。
(この次の記事で”トルク係数”が出てくるが、こちらは、”入力するトルク” 対 ”軸力”の関係を示す定数。あまり混同する事はないが、ともに線形一次の関係なので、ふとした時にあれ?とならぬよう。。。)
締付け線図の見方
トルクの追加した時の線図の動き
さて、締付け線図の見方について
ねじにトルクを追加で入力をし、軸力が F0 -> F1 に上がったとする。
弾性域での使用を前提としフックの法則にしたがっているので、それに伴う変位は線形一次のまま。また、バネ定数を示す線図の傾きは一定値。
つまり、軸力の増加後の状態を線図上で再描写するには、伸び側、縮み側の線図の傾きを一定のまま、平行移動させればよい。
ここで、現れるねじの伸び量と被締結体の縮み量は、当然F1/F0と同じ率で増加する。
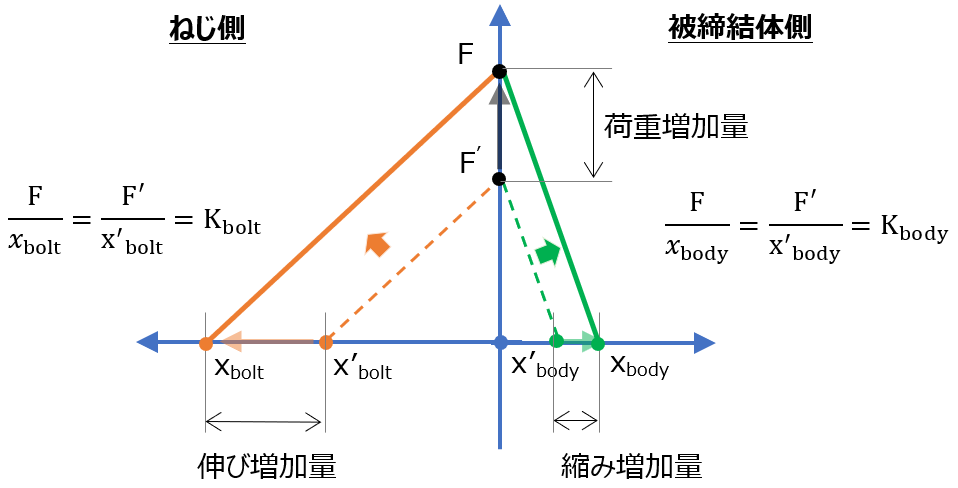
ばね定数違いによる軸力の変動
上の例は、トルク追加の場合に締め付け線図上であらわれる変化(傾き Kbolt は一定で動く)。
続いて、ボルト違いによりばね定数 Kboltが異なる場合。
この場合の軸力変化に与える影響の差異を、締め付け線図上で見る。例として、同一量のねじの伸びが減少した場合(摩耗 / へたり等による)を考える。
ばね定数 Kbolt が異なる場合の様子を示した締め付け線図が以下。
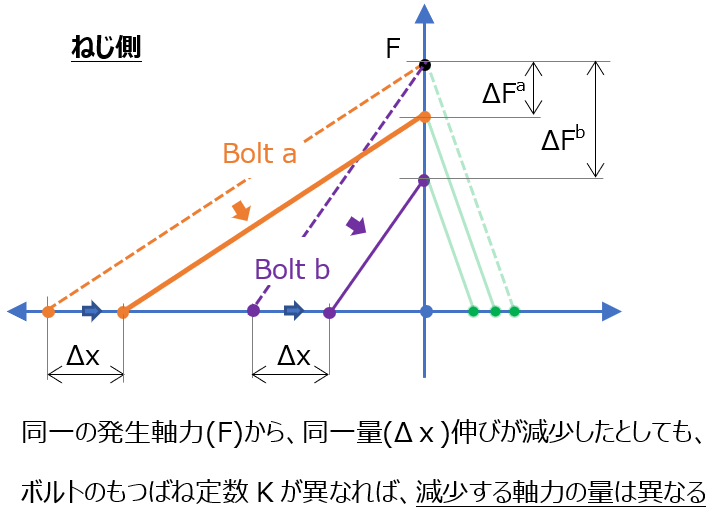
へたり/摩耗量を同一(Δx)としても、ばね定数 Kbolt 違い(伸び代部の設定違い)により軸力の低下に差がある事が線図上に現れる(ΔFaとΔFb)。
-> 同一の摩耗/へたり量でも、ばね定数が低い方が軸力の変化量は小さい= ねじの緩みタフネスは高い
つまり、締結としては安定している事を意味している。
”ねじの原理と設計” には、へたり係数 Zでの説明があるが、上のΔFaとΔFbの差がある事を感覚としてつかんでおけば、この係数への理解は大して困らない(かと)。
一例
補足に一例を。
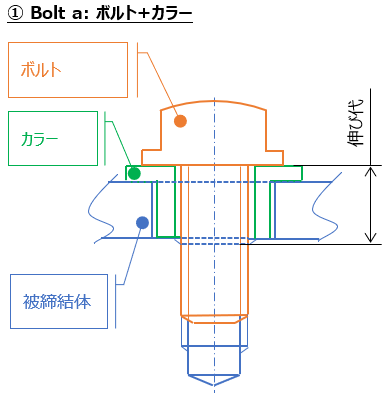
樹脂物(プラスティック系部品)の固定する場合の以下の二通りの締結構成。
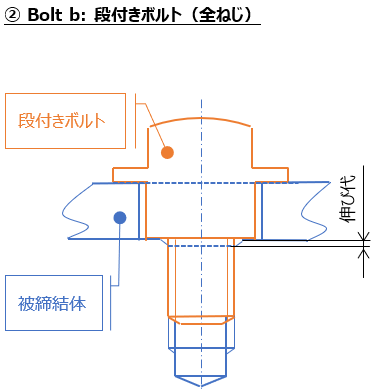
①はボルト+カラーを用いての固定、②は段付きボルトのみでの固定。
(例えに使いたいだけなので、ボルト頭部形状の弾性の差異はここでは無視。伸び代部のみに着目。。。)
①②共に、軸力を発生させる事については問題はないが、②の段付きボルトの設定においては、伸び代が明らかに小さい(めねじの不完全ねじ部のみ)、つまりバネ定数が①に対して高い
つまり、締結時は同等の軸力を発生させる事ができるが、一旦被締結体との間に摩耗/馴染みが発生し伸び代が低下した場合、②の方が軸力喪失が容易に起きる。
つまり緩みやすい。
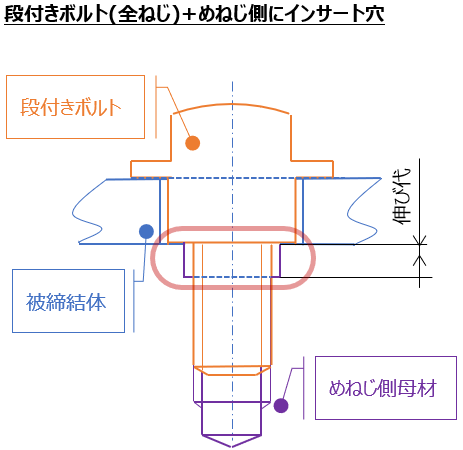
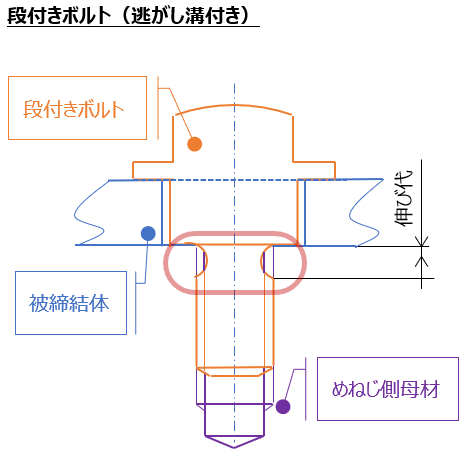
まぁ②の設定は極端な例。。。ほとんどの場合、以下の様な伸び代を確保する設計がされている。
一見、不完全ねじ部の勘合処理のため / ねじ加工のためには見えるが、この加工深さ(巾)についてはゆるみタフネスを上げるためのばね定数(Kbolt)への配慮を意図している事が多い。
もちろん、伸び代の少ない設定であっても必ずNGというわけではない(ゆるみタフネスが弱い事は間違いないが、緩まなければOK)
続いて、最後に”内外力比”について
内外力比
内外力比 概要
締結部に外力が入力された場合を考える
(締結体軸方向への外力)。
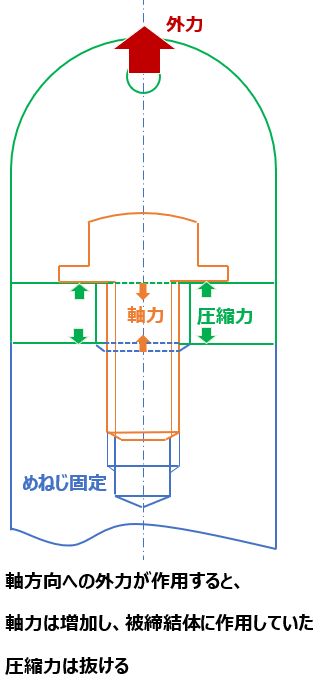
この時入力される外力(Fex)は、軸力の増加分(ΔFbolt)のみならず、被締結体の圧縮力の減少分 (ΔFbody)も負担し、その二つの合力とつり合う。
Fex = ΔFbolt + ΔFbody
つまり、入力した外力(Fex) 全てが軸力に変換されるわけではない。
内外力比
さて上記における入力した外力(Fex )に対する軸力の変化(ΔFbolt )、この二つを比(φ)で表した
- φ = ΔFbolt / Fex
を、内外力比とよぶ。以下に図示する。
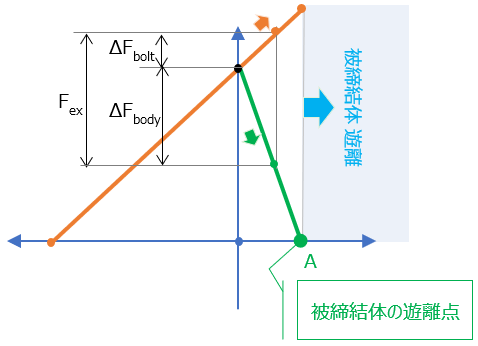
単純に、内外力比が小さければ、外力の入力に対する軸力の変化は小さい。
(逆に、内外力比が大きければ、軸力変化は大きい)
また、一定以上の外力入力された場合は(上図の点Aを超える外力)、被締結体は圧縮力を失うため遊離する。
結果、締結体同士にてずれが発生し、そのずれによりゆるみ等が発生し問題の一因となる。
追記
つづいて、ねじの強度区分、入力トルクと軸力の関係について
以下の記事にて