はじめに
軸力の計算時に用いるねじ面にかかるトルクの計算には、”斜面の定理”と ”摩擦角” を利用する。
詳細はこちら
さて、非常に基本的なトコロなんだけど、式の中で斜面の角度に摩擦角が混ざると、あれ。。なんでだっけ?となった記憶があるので再整理。
まずは摩擦角
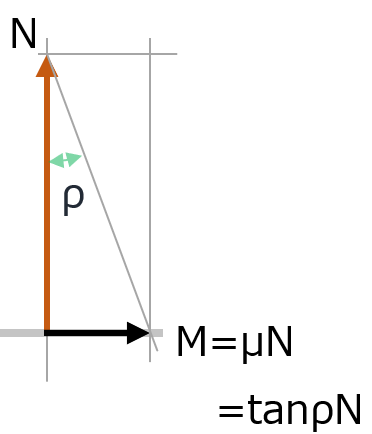
摩擦角:ρ0
摩擦角とは単純に摩擦係数を角度を使って表現したもの。
つまり、物体にかかる垂直方向の地面からの反力Nと摩擦力Mの関係において、MとNから構成される直角三角形の一つの角 ρ(右図)を摩擦係数の代わりに使う。
M=μNより、μ=M/N
つまり、μ=tanρ
至ってシンプルだが、摩擦係数μは ρ を使えば tanρ とも書けることがわかる。
斜面上の物体で、この摩擦角の意味を再度。
重力をF、この時の摩擦力をM、斜面に垂直方向に働く物体の反力をN、静止摩擦係数をμ、斜面の角度ρとして、斜面上の物体に作用する力を図示すれば
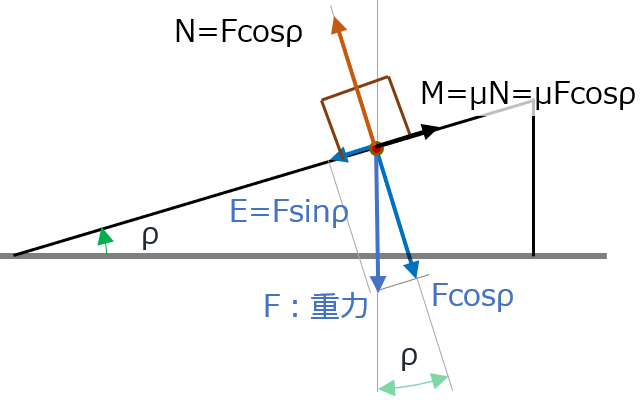
斜面をずり落ちる方向に働く力E以上に摩擦力Mが働いていれば、物体は斜面上に停止する(E<Mである)
ここで、斜面の角度自体が上がっていく場合を想定してみる。
この時、物体がずり落ちる瞬間の斜面の角度をρ0とする。力の釣り合いは E=M、つまり
F・sinρ0 =μ・F・cosρ0 より
μ= F・sinρ0 / F・cosρ0 = tan ρ0
これが摩擦角。つまり、静止摩擦係数μは、斜面の角度 ρ0 の正接 ” tanρ0” で表すことができる。
斜面の定理と摩擦角
さて、 今度は斜面角θ をもつ斜面上に物体が停止しているとする。つまり θ ≦ ρ0
また、静止摩擦係数μは前章と同じとする( μ= tan ρ0 )。
この状態から物体を押し上げる(下げる)ために必要な力Uを考える。
(ここで、Uは水平方向で設定 ∵ねじトルクにより発生する力が水平方向のため)。
物体を斜面に沿って押し上げる時にかける水平方向の力U
物体を押し上げるために加える水平方向の力をUとする
この力Uと重力Fとの合力をSとする。
このSの反力の斜面直方向の分力をNとし、Sの反力とNのなす角をρとする。
図示をすれば
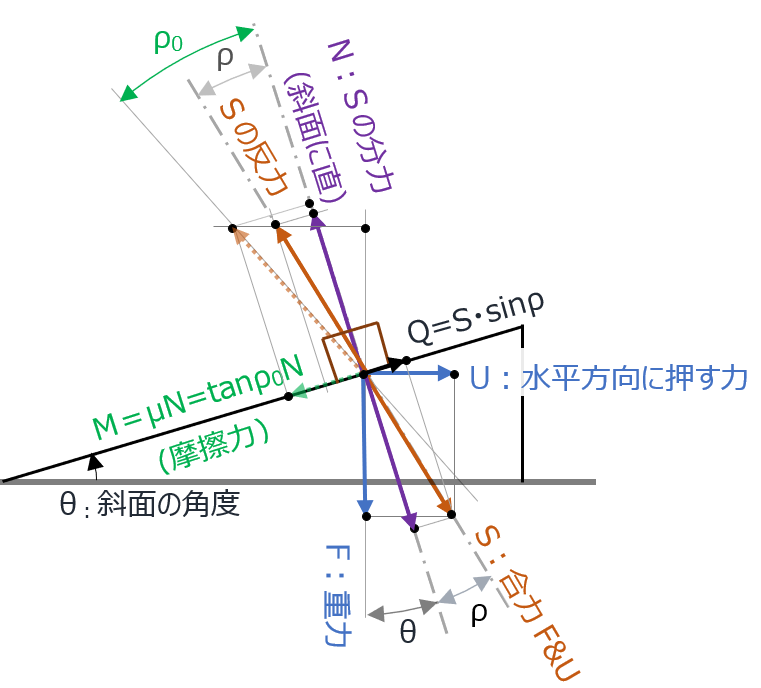
である。
この時、FとUは U= F tan( θ + ρ) であり、
- 斜面方向のSの分力Qは、Q = S sinρ
- 摩擦力Mは、M = μN = tan ρ0・S cosρ
(N=S cosρ、μ= tan ρ0より)
である。
ここでUを増加させる。
Q≧Mとなれば 物体が動き始める。
上記の式を代入すれば、S sinρ ≧ tan ρ0・S cosρ を満たすとき。整理して、
- tanρ ≧ tan ρ0 (ρは斜面を前提にしているので、0≦ρ≦π/2)
つまり、水平方向の力Uの増加に伴って増加する角度ρが、摩擦角ρ0以上になった瞬間に、物体は動き出す。
これから物体が動き出す時のFとUの関係は、上図の中のρがρ0となった時。つまり
- U= F tan( θ + ρ0)
を満たす事。
さてこの先、これがねじ面の軸力計算に展開される(F:軸力 & U:トルクにより発生する力)。
(もう一工夫必要ではあるが(後述))。
また押し上げる時の式は、締結で言えばねじを締める時の関係式のベースになる。
ついでに物体を斜面に沿って押し下げる場合も
物体を斜面に沿って押し上げる時にかける水平方向の力U
考え方は同じ。図示すれば、
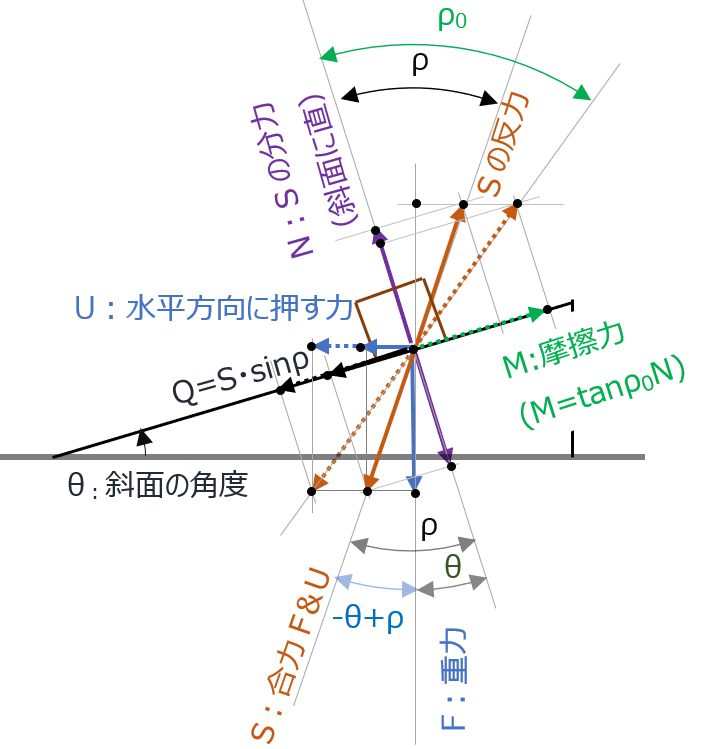
同様にQ≧Mの時、物体が動き出す。この時のFとUの関係は、
- U= F tan( – θ + ρ0)
この物体を押し下げる時の式は、締結で言えばねじを緩める時の関係式のベースになる。
ねじ面における斜面の定理
さて上述の関係式を、ねじ面に展開をするのにちょっややこしいのは、上述のような斜面が一つの傾斜角θではなく、
- ねじの山角 から導かれる斜面角度:α
- ねじのリード角:β
の合成した角度の斜面となっている事。(バンク角のついた坂道みたいなもの)
この合成した角度の斜面上において、物体を押し上げる関係式(水平方向にかける力UとFの関係)が必要。
ちょっと長くなりそうなので、次の記事にて