 ベクトル
ベクトル [ベクトル]4. 座標系の定義:ベクトルの正規直行性と内積の利用(回転行列の入り口)
空間の基底となる n本すべてのベクトルがお互いに直行し、かつ正規性を持つ場合、このn本のベクトルをn次元空間の正規直行基底という。座標軸とベクトルを組み合わせるのに使える(内積を使った座標値の算出)のだが、もうちょっと展開すれば、座標軸変換(回転行列)の入り口までの流れが、これを起点につかむ事ができる。
 ベクトル
ベクトル  ベクトル
ベクトル  ベクトル
ベクトル  ベクトル
ベクトル  指数・対数
指数・対数  指数・対数
指数・対数  基礎関数・公式
基礎関数・公式  指数・対数
指数・対数 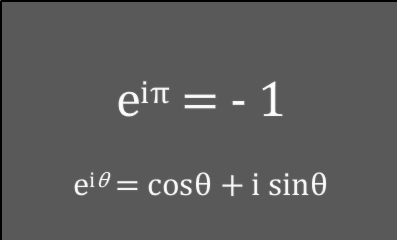 基礎関数・公式
基礎関数・公式