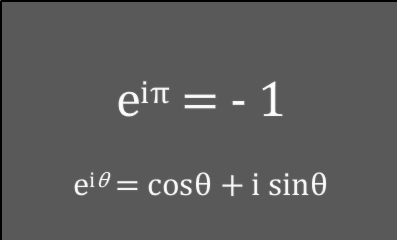オイラーの公式 2. オイラーの公式 : 世界で最も美しい公式の導き方
オイラーの公式は、基本、指数関数(e^θ) と 三角関数(sinθ、cosθ)の等式化であるが、ただこれを関連付ける時に、e^θ、sinθ、cosθ の各々3つが持つ一般的な性質を, マクローリン展開（級数展開）を利用して見事に組み合わせている。この成立過程も非常に美しい。このあたりの話を。。。
数学（高校）
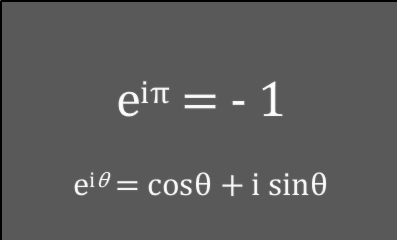オイラーの公式 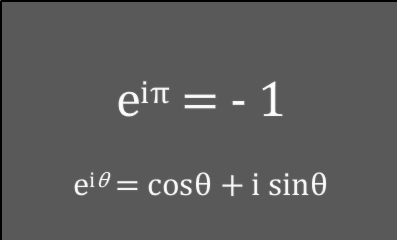オイラーの公式 1. オイラーの公式 : 世界で最も美しい公式の見かた、使いかた
世界で最も美しいといわれる式 e^(iπ)=-1 はオイラーの公式 e^(iθ)= cosθ + i sinθ から算出される。このオイラーの公式の背景が美しいと言われる根拠とこの式のその使われ方を少し。美しい公式だね” だけでは、ちょっともったいない
座標・単位・基礎関数 4. sin x と cos x のたし算 と ひき算
はじめに\(sin x \) と \(cos x \)のたし算・ひき算、つまり\( a \cdot cos x ± b \cdot sinx \) の型の三角関数は、\( \sqrt{a^2+b^2} \cdot cos(x ̠∓ θ ) ...
座標・単位・基礎関数 3. 三角関数：加法定理はベクトルの内積計算と同じ
ベクトルの内積として三角関数の加法定理をみれば、そのしくみは簡単にわかる（図でも書いてみれば、そりゃそうか。。。の一発理解レベル）
座標・単位・基礎関数 2. 角度単位 ”ラジアン”が便利な理由
日常の角度表示と違い（度数表示：90°とか360°とか）、数学、物理ではラジアン表示（π）が主に使用される。圧倒的に使い勝手が良いからである。ラジアン表記の意味と使い勝手の良いところを説明。ラジアンの値は、ｒ＝１の円(周長：2π)を、中心角Θで切り取った時の ”円弧の長さ” である。
座標・単位・基礎関数 1. 座標軸→ピタゴラスの定理→三角関数→極座標まで
工学で使用される座標軸の定義と極座標の定義の話。極座標は定義を忘れないように、はじまりのピタゴラスの定理から三角関数の話、極座標の定義への利用までの流れまでの覚書
ベクトル 2. ベクトルの内積の意味とその計算
ベクトルの内積をまとめて簡易説明。内積の意味と定義から、成分計算の導き方、簡単な使い道まで。
ベクトル 1. ベクトルとは？から
ベクトルとは”大きさ”と”向き”を同時に持つ量、基本はこれだけだが、複数情報を一つの形で持つことができ、またそのままの形で計算可となるため、数学、物理にて多用される（ベクトル計算後に成分値算出等々）。
対数 1. 対数の基本的な見方：対数のしくみと足し算、引き算について
対数も指数の特徴を踏まえれば特に新しい事はない。対数と指数の関係からその基本的な性質、ついでに対数の足し算＆引き算について、底の入れ替えについても