10乗数の指数が小数を持つとき
前の記事は、指数の四則演算と指数の分数・小数・マイナスについて
この中で以下を踏まえる事と、
あわせて、小数点以下の指数が示す値をざっくりと覚えておけば
102.7 <- だいたい500ぐらい、、、
104.3 <- だいたい20,000ぐらいかな
と、イメージできる様になると書いた。
例えば102.6は、
- 102.6=100.6+2 =100.6x 102・・・①
から、”100.6(≒ 3.9810・・・)を100倍(102倍)”した値。
よって 102.6≒ 398.1
こんな感じで、元の値が大体わかるようになる。
で、その時に使う”指数の小数点以下の値の目安”はこれ↓
\( \small 10^{0} ~~ =1.0000・・・( 10^\frac{0}{10}= \sqrt[10]{10^0} \) )
\( \small 10^{0.1}=1.2589・・・( 10^\frac{1}{10}= \sqrt[10]{10^1} \) )
\( \small 10^{0.2}=1.5849・・・( 10^\frac{2}{10}= \sqrt[10]{10^2} \) )
\( \small 10^{0.3}=1.9952・・・( 10^\frac{3}{10}= \sqrt[10]{10^3} \) )
\( \small 10^{0.4}=2.5119・・・( 10^\frac{4}{10}= \sqrt[10]{10^4} \) )
\( \small 10^{0.5}=3.1623・・・( 10^\frac{5}{10}= \sqrt[10]{10^5} \) )
\( \small 10^{0.6}=3.9811・・・( 10^\frac{6}{10}= \sqrt[10]{10^6} \) )
\( \small 10^{0.7}=5.0119・・・( 10^\frac{7}{10}= \sqrt[10]{10^7} \) )
\( \small 10^{0.8}=6.3096・・・( 10^\frac{8}{10}= \sqrt[10]{10^8} \) )
\( \small 10^{0.9}=7.9433・・・( 10^\frac{9}{10}= \sqrt[10]{10^9} \) )
\( \small 10^{1.0}=10.000・・・( 10^\frac{10}{10}= \sqrt[10]{10^{10}} \) )
見ての通り指数部分の小数部は一定割合の増加しても、その乗数が示す値の増加は一定割合ではない(指数関数)。
上の例のとおり10の乗数の
・指数部分:0.3ぐらい -> 元の値:だいたい 2 (100.3≒2)
・指数部分:0.7ぐらい -> 元の値:だいたい 5(100.7 ≒ 5)
・指数部分:0.9ぐらい -> 元の値:だいたい 8(100.9≒ 8)
桁内の真ん中の ”5”が指数を使うと”0.7”ぐらい、と覚えておけば、そこそこ指数の値から元の値をざっくりイメージできるようになる(かな)。
任意の値の確認はこちらで。。。
追記1:任意の値を10の乗数(小数点付き)で表す
(同じ例(398.1)を使い、)10進法の桁毎で書くと
- 398.1 = 3x102 + 9x101 + 8x100 + 1x10-1・・・②
(102の位:3、101の位:9、100の位:8、10-1の位:1)
前章にて
- 398.1 =102.6=100.6x 102・・・①
(102の位:100.6)
と書いたが、①式を②式と同じようにみれば、①式は元の値を102の位のみで表し、かつその102の位の値は100.6(10のべき乗)にて表示したもの、としているだけ。
これを、
- 398.1≒ 1x102.6・・・②
とかけば、 小数点まで使えば”指数のみにて任意の値が表現できる”事がわかる(この例だと10の2.6乗)。
また、この指数部分のみで任意の値を表したのが対数。
追記2:対数もついでに
常用対数(log10X)について少し追記。
同じ例をつかえば、398.1は102.6…の位の値と等しい。つまり任意の値は指数部分のみでも表現する事が可能。
これを表現するのが対数、log10398.1≒2.6と表す <-これが常用対数
対数の性質についてはこちらの記事が覚書
この見方で、10を底にもつ常用対数(Y=log10X)がイメージしやすくなる。(指数の四則演算の特徴がつかめていれば、対数の計算にもそれを元に考えればよいだけ。)
また、片対数グラフのY軸密度の偏りがありそれが繰り返すのは(下図参照)、整数部分は桁数を示しているだけなので、桁が上がる毎にリセットされて、密度の偏りが繰り返す(当たり前といえば当たり前)
(密度に偏りがあるのは、実数の時の数字の密度と指数表示にした時の密度に差があるため:100.7 ≒ 5と同じ話)
\( \small 10^{0} ~~ =1.0・・・・・( 10^\frac{0}{10}= \sqrt[10]{10^0} \) )
\( \small 10^{0.1}=1.2589・・・( 10^\frac{1}{10}= \sqrt[10]{10^1} \) )
\( \small 10^{0.2}=1.5849・・・( 10^\frac{2}{10}= \sqrt[10]{10^2} \) )
\( \small 10^{0.3}=1.9952・・・( 10^\frac{3}{10}= \sqrt[10]{10^3} \) )
\( \small 10^{0.4}=2.5119・・・( 10^\frac{4}{10}= \sqrt[10]{10^4} \) )
\( \small 10^{0.5}=3.1623・・・( 10^\frac{5}{10}= \sqrt[10]{10^5} \) )
\( \small 10^{0.6}=3.9811・・・( 10^\frac{6}{10}= \sqrt[10]{10^6} \) )
\( \small 10^{0.7}=5.0119・・・( 10^\frac{7}{10}= \sqrt[10]{10^7} \) )
\( \small 10^{0.8}=6.3096・・・( 10^\frac{8}{10}= \sqrt[10]{10^8} \) )
\( \small 10^{0.9}=7.9433・・・( 10^\frac{9}{10}= \sqrt[10]{10^9} \) )
\( \small 10^{1.0}=10.000・・・( 10^\frac{10}{10}= \sqrt[10]{10^{10}} \) )
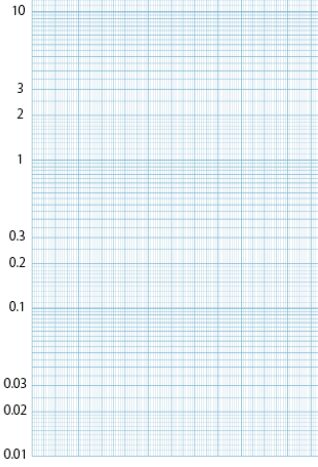
(桁数が変わるたびに繰り返される)
指数の見方のときにも書いたが、実数には数字の密度の偏りはないが、それを指数表示にすると表示上の密度に偏りができる。この偏りと密度の繰り返しが、片対数グラフのy軸に現れる。
と、これが10の乗数を見る時のざっくり感覚(と対数)
ちなみに、”指数表示での値の密度 ” 対 ”実数表示での値の密度 ” の違いに対する感覚は、ある程度あるといいかもしれない。
(例えば、指数であるデジベル(dB)表示の値とか。。消音対策で、99dBから-2dB減衰と 93dBから-2dB 減衰では、同じ-2dB減衰でも実際に減衰させる音圧レベル違うよなぁ、、とかとかの感覚。)