はじめに
三次元上の空間における質点の移動を考える。質点が任意の方向に動くとき、その軌跡は曲線を描く。
(任意の点の移動:自由度3(空間上の拘束なし))
さて、この点の動く方向は、曲線に対して接線方向、法線方向、従法線方向の三方向にて表現できる。
慣性力方向で例えるならば、接線方向は点の進行方向であり、加減速時の慣性力の発生方向、法線方向は遠心力の発生方向、従法線方向はジャイロモーメントを発生させる慣性力の方向である。
以下は、この三方向のベクトル表記について
曲率
まずは曲線の曲率から
単位ベクトル \( \vec{i} , \vec{j} , \vec{k} \) をそれぞれX、Y、Z軸の方向ベクトルとする。
質点が点Aを出発し点Pまで移動した時、点A->点Pまでの空間曲線の長さを s とし、点Pの座標を s の関数
\( ( x(s) , y(s) , z(s) ) \)・・・⓪
と表す。これを使って 点Pの描く曲線はベクトルを使い
\( \vec{r(s)} = x(s) \cdot \vec{i}+y(s) \cdot \vec{j}+z(s) \cdot \vec{k} \)・・・①
にて表す事ができる。
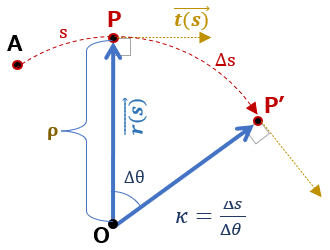
さて、ここで、点Pから点P’までに進む間に接線が回転する角度を\(\Delta \theta \)とし、その間に進んだ角度\(\Delta s \)の比 \(\kappa \) を考える。
\(\kappa = \displaystyle \lim_{\Delta s \to 0} \frac{\Delta \theta}{\Delta s} =\frac{d\theta}{ds} \) ・・・②
\(\kappa \) を、この曲線のこの点における曲率という。
\(\Delta \theta \) が充分に小さいときは、PP’ は円弧に近似できる。よって、OPの長さをρとすれば、\( ds = \rho \cdot d \theta \) 、これを使って
\(\kappa =\displaystyle \frac{d\theta}{ds} =\frac{d\theta}{\rho \cdot d \theta} =\frac{1}{\rho} \) ・・・③
この ρ は曲率半径と呼ばれる。
これを使えば質点が自由な曲線を描いていたとしても、瞬間的には曲率半径 ρ の円弧上を進んでいると見なして取り扱う事ができる(もちろん曲率は随時変わるが、、)。
接線ベクトル
曲線における接線ベクトル方向とは、質点の動きで言えば物体のその瞬間の進行方向。
接線ベクトルを求める
点P の描く曲線は、空間曲線の長さ s を使い \( \vec{r(s)} \) で表す。
\( \vec{r(s)} = x(s) \cdot \vec{i}+y(s) \cdot \vec{j}+z(s) \cdot \vec{k} \)
また、点Pから Δsだけ進んだ点を点P’とする。
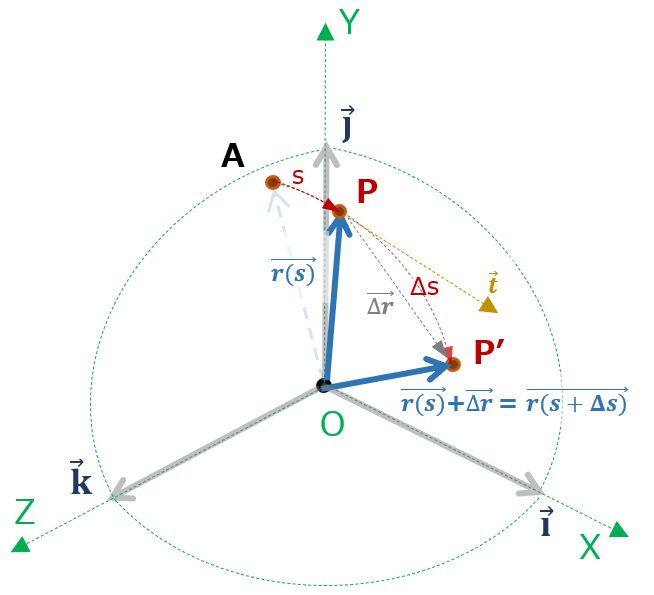
曲線 \( \vec{r(s)} \) の s における接線方向は、\( {\Delta s} \) が 0 に近づいた時のPP’ 方向。つまり、図①の\( \vec{\Delta r} \)。
ここで、\( \vec{r(s)}+\vec{\Delta r} = \overrightarrow{r(s+\Delta s)} \) を使って
\( \displaystyle \lim_{\Delta s \to 0} \frac{\vec{\Delta r}}{\Delta s} = \displaystyle \lim_{\Delta s \to 0} \frac{\overrightarrow{r(s+\Delta s)} – \vec{r(s)}}{\Delta s}=\frac{d\vec{r(s)}}{ds} \) ・・・④
つまり、\( \vec{r(s)} \) のsにおける微分値。この接線ベクトルを \( \vec{t(s)} \) とかけば、
\( \vec{t(s)} =\displaystyle \frac{d\vec{r(s)}}{ds}=\overrightarrow{r'(s)} \) ・・・⑤
さて接線ベクトルの大きさは、sinθ=θ(θ:充分に小) を使えば
\(
\begin{align}
|\vec{t(s)}| &=\displaystyle |\frac{d\vec{r(s)}}{ds}|=|\lim_{\Delta s \to 0} \frac{\vec{\Delta r}}{\Delta s}|
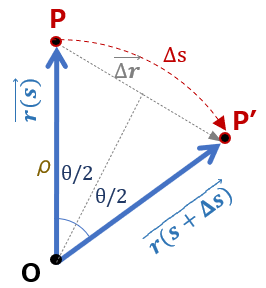
=\lim_{\Delta s \to 0} \frac{\overline{PP’}}{\stackrel{\huge\frown}{PP’}} \\[8pt]
&=\lim_{\Delta s \to 0} \displaystyle\frac{2\cdot \rho\sin ( \displaystyle\frac{\theta}{2}) }{\rho\theta}
=\lim_{\Delta s \to 0} \displaystyle\frac{2\cdot\rho ( \displaystyle\frac{\theta}{2})}{\rho\theta}=1
\end{align}\\[8pt]
\)
\( |\vec{t(s)} |=|\overrightarrow{r'(s)}|=1 \) ・・・⑥
である。
つまり、空間長sで曲線を定義すれば、その微分値から導かれる接線ベクトルは単位ベクトルとなる。
(変数を空間曲線の長さ s ではなく)任意の変数uででとる場合接線方向の算出に対する微分の定義は同じ。
(例:(x(u), y(u), z(u))として、曲線を r(u) = x(u) i + y(u) j + z(u) k )
この場合、接線ベクトルは単位ベクトルで算出されない。接線ベクトル \( \vec{t(u)} \) を、単位ベクトル(正規化)として定義するのであれば、
\( \vec{t(u)} =\displaystyle\frac{\overrightarrow{r'(u)}}{|\overrightarrow{r'(u)}|} \) ・・・⑦
法線ベクトル
曲線における法線ベクトルとは、質点の動きで言えば遠心力が発生する方向。
前章と同じ設定にて、 空間曲線の長さ s を使い、 r(s) を点P の描く曲線とする。
r(s) = x(s) i + y(s) j + z(s) k
また、前章同様に点Pから Δsだけ進んだ点P’とする。
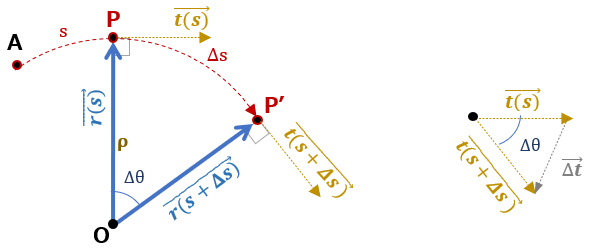
さて、質点が曲線上の向きを変えながら進むという事は、接線ベクトル方向が変化する事を示す。
このsの変化に伴う以下の接線ベクトル t(s) の変化 Δ t を考える。
\( \overrightarrow{\Delta t} = \overrightarrow{t(s+\Delta s)}-\vec{t(s)} \)・・・⑧
Δ t のsにおける瞬間の変化をn(s)とすれば、微分を使い
\( \vec{n(s)}=\displaystyle\lim_{\Delta s \to 0}\frac{\vec{\Delta t}}{\Delta s}
=\displaystyle\lim_{\Delta s \to 0}\frac{\overrightarrow{t(s+\Delta s)}-\vec{t(s)}}{\Delta s}
= \displaystyle\frac{d\vec{t(s)}}{ds} \)・・・⑨
ここで、⑤式を使えば、
\( \vec{n(s)}= \displaystyle\frac{d\vec{t(s)}}{ds}
= \displaystyle\frac{d}{ds}(\frac{d\vec{r(s)}}{ds}) = \overrightarrow{r”(s)}\)・・・⑩
また、その大きさは \( |\overrightarrow{\Delta t}| = |\overrightarrow{t(s+\Delta s)}-\vec{t(s)}|≒ |\vec{t(s)}|\Delta\theta =\Delta\theta \) を用いて、
(∵ |t(s)| = 1 )
\( |\vec{n(s)}|=|\displaystyle\lim_{\Delta s \to 0}\frac{\vec{\Delta t}}{\Delta s}|
=\displaystyle\lim_{\Delta s \to 0}\frac{{\Delta\theta}}{\Delta s}
= \displaystyle\frac{{d\theta}}{ds}
=\kappa= \displaystyle\frac{{1}}{\rho} \)・・・⑪
n(s) の方向は、定義からΔsが0に近づいた時のΔt 方向であり、接線ベクトルt(s) に垂直(曲線は瞬間的には円)。つまり、内積は
t(s)・n(s) =0 ・・・⑫
n(s) を点Pにおける曲線の(主)法線ベクトルという。
つまり、
従法線ベクトル
従法線ベクトルは質点の動きで言うと、ジャイロモーメントを発生させる慣性力が発生する方向。
質点の動きは三次元。進行方向である接線ベクトル、それに直角方向である法線ベクトルに加え、もう一方向、双方に直角方向な方向のベクトルがある。
この残りの一方向が 従法線ベクトルの方向。
従法線ベクトルを b(s) とすると、その方向は t(s) と n(s) の双方に直角であるため、外積を使えば定義できる。
t(s)は単位ベクトル、n(s)は単位ベクトル化して ρn(s) 。これらを使い b(s) も単位ベクトルで出力すれば、
b(s) = t(s) X ρ n(s) ・・・⑬
⑤、⑩式を使えば、
b(s) = ρ ( r‘(s) X r”(s) ) ・・・⑭
である。
補足:空間曲線の長さ s
( x(s), y(s), z(s) ) ・・・⓪
r(s) = x(s) i + y(s) j + z(s) k ・・・①
で使った”空間曲線の長さ s”について、ちょっと補足。
一言で言えば、質点が”実際に動いた距離”の事であるが、イメージがつかみにくかった記憶があるので、例を使って。
XY平面上のr=1の円の曲線上の座標は、 (x(θ), y(θ), z(θ)) =(cosθ, sinθ、0)
よって、 r( θ ) = cosθ i + sinθ j + 0・ k
この時のθを(角度ではなく)”空間上の円弧の長さ” そのものと捉えれば、これが空間長。
つまり、⓪式、①式でいう空間長sにあたる。
( ”ラジアン表記した角度θ”=”半径1の円から切り取った弧の長さ”より) (Link)
回転体の速度算出等にも同じとらえ方(Link)ができるようになれば、直線での定義が曲線にも使え理解しやすい。