はじめに
前回の記事は命題(主張)の定義とその型の言い換えによる誤りについて
今回はベースの三段論法、そこに入り込む詭弁について。論理的に聞こえる話でも、ごまかしを入れる事自体は意外と簡単。
まっとうに聞こえる説得/説明だとしても、注意しておくといい事がある。
(根拠/前提をしめして、そこから推論/結論をいうみたいな話の流れは結構あるかと)
詭弁の入り込んでいるかどうか気づくのに、簡単にできるのは以下の4つ
- 前提が ”~でない” + ”~でない” ときたら、結論は ”断定できない”
”あいつは○○ができない”、”あいつはxxもできない”、よって”あいつは何もできない” は、(心理的な話は別として、、)演繹的推論としては成立していない。”あいつは何もできないかもしれない”であれば、帰納的推論としては成立。 - 前提が ”ある~” + ”ある~” ときたら、結論は ”断定できない”
”一部の金持ちはうそつきである”、”あのビルの住人のおおくは金持ちである” よって、”あのビルの住人の一部にうそつきがいる”は、結論だけ切り取れば、そんな人もいるだろうと”真”っぽく見えるが演繹的な推論推論としては成立していない(この場合も、帰納的推論結果である ”いるはず” の仮説まで。全員うそつきの可能性もあるし、全員正直者の可能性もある)。 - 前提のどちらかが ”~でない” できたら、結論は必ず ”~でない”
- 主語の概念、述語の概念、媒概念がどの命題においても同じ意味になっている事
(正確な言葉で定義されているかの確認)
これの説明に、まずは三段論法の定義と基本からはじめて、次に上の詭弁の入り込む余地について。
三段論法の定義とその基本から
三段論法の基本
ある前提から結論を導くために理詰め(演繹)の推論する時に、用いられるのが三段論法。
つまり、2つの命題が論理的に正しくつながっている、かつすべての前提が”真”であれば、結論は常に”真”。
また、この中の媒概念とは
三段論法は、
- S:結論で ” 主語 ” となる概念
- M:”結論で消える” 媒概念 ”
- P:結論で ” 述語 ” となる概念
をつかって、二つの命題 (大前提(第一段)、小前提(第二段))から、最後に” S (主語) ならば P (述語) ” の結論(第三段)を得る三段階の形態をとる。
第一格(格については後述)を例にすれば
- 第一段(大前提)・・M -> P ( M(媒概念)ならば、P(述語)である。)
- 第二段(小前提)・・S -> M ( S(主語)ならば、M(媒概念)である。)
- 第三段(結論) ・・ S -> P ( ゆえに、S(主語)ならば、P(述語)である。)
具体的にはこんな感じ
この三段論法には、
- 各段の言い換えから発生する ”三段論法の格”
- 前述の(肯定文or否定文)/(全称文or特称文)の組み合わせ違いによる”主張の型”
による組合せがある。
三段論法の格と主張の型
三段論法の格として、前提の各段(第一段&第二段)の組み合わせ違いにより、以下の計4格存在する。
注:第三段(結論)は、全て ”S->P” (S(主語)ならば P(述語)である)
(ちなみに、第一段が ”M(媒概念)とP(述語)” & 第二段が ”S(主語)とM(媒概念)” の組合せ)
この各段に、命題(主張)の型(全称文or特称文、肯定文or否定文)(前述)
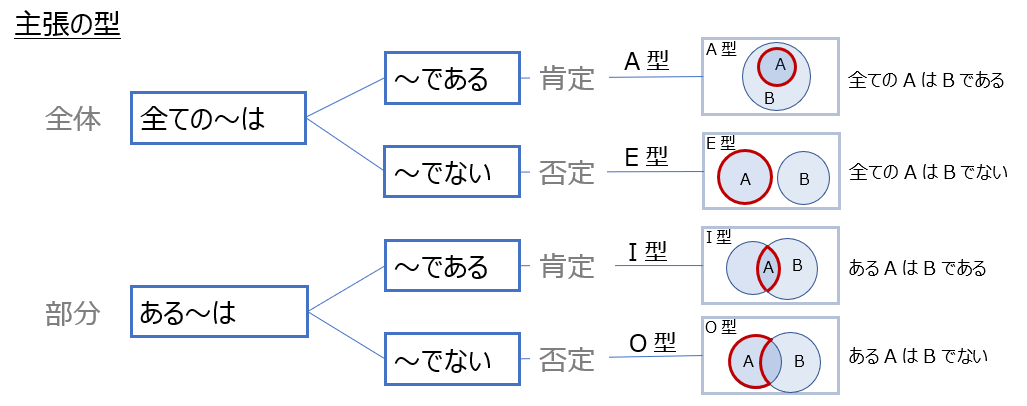
が組み合わされる。
格と型の組合せ合計で256通りの内、論法として正しく結論が導けるのは24通りのみ。
( 全256通り= 格4(三段論法の格が4通り)x型43(主張の型が各4通りで三段の組み合わせ))
で、正しい結論となる24通りの組み合わせは、
- 第一格:AAA (AAI) EAE (EAO) AII EIO : 常に真x4通り + 弱勢式(結論がIかOでも成立)x2通り
- 第二格:EAE (EAO) AEE (AEO) EIO AOO : 常に真x4通り + 弱勢式(結論がIかOでも成立)x2通り
- 第三格:AAI EAO IAI AII OAO EIO : 常に真x6通り
- 第四格:AAI AEE (AEO) IAI EAO EIO : 常に真x5通り + 弱勢式(結論がIかOでも成立)x1通り
の24通り。
Note: ちなみに見方としては、例えば 第一格の ”EIO” が正しい結論を導く組合せに入っているが、この組み合わせは
- 第一段(大前提)が ”E” 型 :全てのMはPでない (全ての時間つぶしは、仕事ではない)
- 第二段(小前提)が ”I” 型 :あるSはMである (ある作業は、時間つぶしである)
- 第三段(結論)が ”O” 型 :あるSはPでない (ある作業は、仕事ではない)
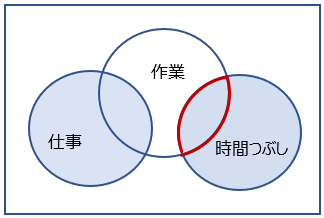
で、EIOとみる(この論法の組合せは、(前提が正しければ)正しい結論)
(ネットでペン図、オイラー図等で検索すると覚え方ふくめ、詳細がイロイロと出てくるのでそちらを)
以上を踏まえ、 つづいて三段論法にごまかしが入り込む余地について。
三段論法の誤り
そもそもの大前提として、三段論法では、すべての前提が”真”であれば、結論は常に”真”。
つまり前提が、必ず”真”でなければならない。ここに曖昧な前提を紛れ込ませれば、結論も必ず”真” にはならない。
この ”前提が必ず真” への注意(確認)は毎度の事として、、、
それ以外にも三段論法の構造上、頭の片隅にいれておいた方がよい点がある。
代表例として二つ。
一つ目が上記の正しい結論を導く組合せ”以外”を使ってしまう例、二つ目が結論で消える”媒概念”にごまかしを入れてしまう例。
この論法間違いに気づくのに、覚えておくと便利なパターンがある。
正しい結論を導く組合せ”以外”を使ってしまう例
組合せが256通りあって、その中で24通りが正しい三段論法と言われたトコロで、覚えきらないし普段使いできるわけゃない。。。
ただいくつか知っておくと、ん?と怪しい匂いに気づけるようになる(嗅覚がちょいと上がる)。
否定二前提の虚偽
(上の正しい組合せで EE-, EO-, OE-,OO- で始まる組合せが”ない”事からもわかるが)、
どの組み合わせでも、前提が二つ(大前提と小前提)とも“否定”の場合、結論は正しいとも誤りともいえない。
-> ”~でない”+”~でない”ときたら、結論は”断定できない”
例えば、
図でかけば、
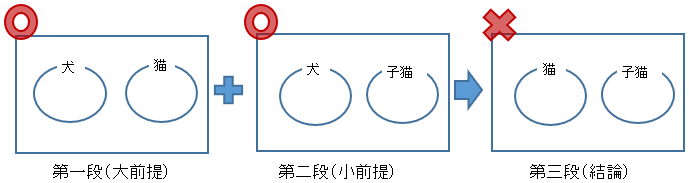
この場合「推論の形式(考え方)として誤り」と見る。
不当肯定の虚偽
どの組み合わせでも、前提のどちらかが否定文であれば、結論も否定文でなければならない。もし結論が肯定文であれば、論法に誤りがある。
-> 前提のどちらかが”~でない” できたら、結論は必ず ”~でない”
例えば、
多くの場合明らかにおかしいため気づく。詭弁には使えない。
特称二前提の虚偽
どの組み合わせでも、前提が二つとも特称文「ある~」の場合、結論の真偽は保証されない。
これも否定二前提の虚偽と同様推論の形式として誤り。
-> ”ある~”+”ある~”ときたら、結論は”断定できない”
例えば、
(そうかもしれないし、そうでないかもしれない。)
(「あるユダヤ人はうそつきではない」 も成立する。つまり、これだけの前提だけでは不十分)
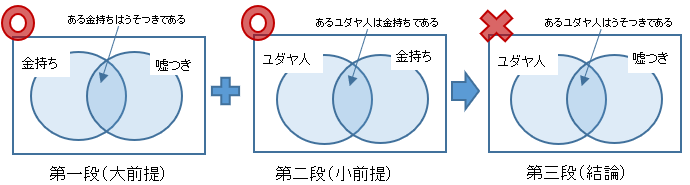
媒概念のごまかし
結論で消える”媒概念”に、ごまかしが紛れ込むと、気づきにくい(論理的っぽく聞こえるけど、言葉に正確性がないがゆえに詭弁になっているパターンって、これが多い)。
媒概念曖昧の虚偽(ごまかし)
媒概念に、二通りの意味を当てはめる事は詭弁となる。例えば、
この場合、媒概念 ”Nothing” に二通りの意味を当て込んでいる。これもよく詭弁で使われる。
いつの間にか使っている言葉の定義(意味)を微妙に変える、これは注意していないと気づきにくい
四個概念の虚偽(ごまかし)
上の媒概念曖昧の虚偽もこの四個概念の虚偽に含まれる。
上の例では、媒概念である”Nothing”(M)に、二つの意味(M1とM2)をもたせて
と三段論法にS、M1、M2、Pの4つの概念を使ったため虚偽となる
(第一段&第二段が正しくとも、M1&M2は第三段の結論で消えるため、結論が偽であっても気づきにくい)。
これと同様に媒概念 M ではなく S,P で二つの意味につかっている場合も当然虚偽となる。
例えば、
大前提の”女”を”一人の女”と正確に定義してあれば立派な三段論法であるが、曖昧な定義が故に結論の”女”に”女遊び”という意味が発生している。これが詭弁(単に日本語の使い方が雑なだけの場合もあるが。。)。
詭弁が含まれていると”おや?”と気づく事が多いが、どこがおかしいのかはすぐにはわからず話に流されてしまう。要注意。
いったんまとめ
ごまかし関連で頭の片隅にいれておくのは、とりあえず以下の4つだけ
- 前提が ”~でない” + ”~でない” ときたら、結論は ”断定できない”
- 前提が ”ある~” + ”ある~” ときたら、結論は ”断定できない”
- 前提のどちらかが ”~でない” できたら、結論は必ず ”~でない”
- 主語の概念、述語の概念、媒概念がどの命題においても同じ意味になっている事
(正確な言葉で定義されているかの確認)
まずは、三段論法の基礎と構造をしっておく、あと、ごまかしがどこから入りやすいかをしっておくのも詭弁に気づく一助になるかと。
さて、三段論法にもそれなりの基本則がある。次の記事にて


