前回の記事は三段論法、それを使った詭弁について
今回は、三段論法の規則（包むという事）の定義と誤りを利用した詭弁について
目次
三段論法内の命題（主張)の規則
命題における概念：”包む”ということについて
一つの命題の概念にて「包まれている」「包まれていない」に考慮することが役に立つ。
概念Xが含まれる場合とは・・・「（全称文）全てのXは～」もしくは「（否定文）～はXでない。」の場合
概念Xが含まれない場合とは・・「（特称文）あるXは～ 」もしくは「（肯定文）～はXである。」の場合
つまり概念Xを概念A＆Bにして、図にかけば
（下線あり：概念が包まれる場合）、
つまり、
主張の型でいえば、
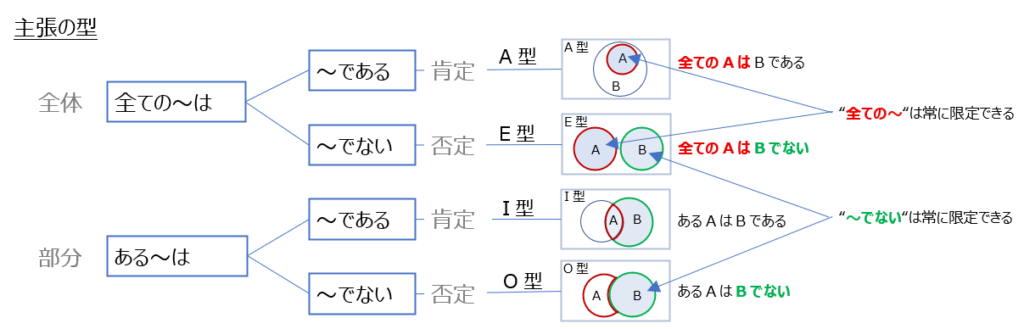
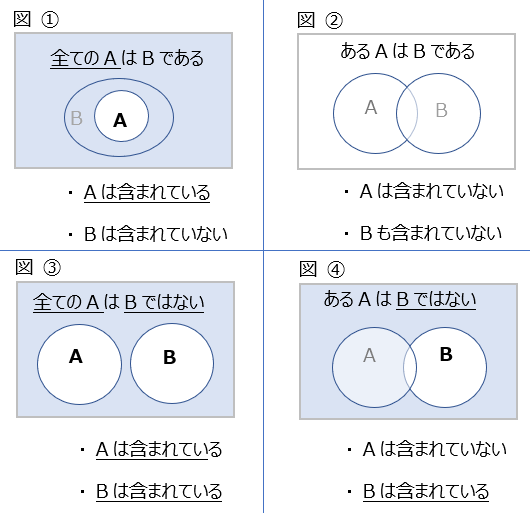
例えば
「ある犬は子犬ではない」（上図④）といった主張の場合、
「ある犬」は（どんな犬かは）限定されていない（＝含まれない）が、「子犬ではない」は子犬ではない事は限定されている（＝含まれる）
「あるトラは白色である」（上図②）という主張になった場合、
「あるトラ」は（どんなトラかは）限定されていない（＝含まれない）、また「白色である」はトラ以外の白色であるモノが含まれるため限定できない（＝含まれない）。
また、
「全ての犬は猫ではない」（上図③）という主張では、
「全ての犬」は全て限定できる（＝含まれる）、「猫ではない」は猫ではない事が限定されている（＝含まれる）
「全ての子犬は犬である」（上図①）という主張では、
「全ての子犬」は全ての子犬は限定されている（＝含まれる）が、「犬である」は子犬以外の犬も含まれるため限定されない（＝含まれない）。
さてさて、これらの命題のつくりを踏まえ、三段論法とした時には次の規則がある。
三段論法を組む時、命題内の概念を ”包む” 事の規則
媒概念を包まない虚偽：媒概念は二つの前提の少なくとも一方で、包まれていなければならない。
もし聞いていても、ん？その話の流れはおかしいだろうと気づきはするが、一応図でかけば、
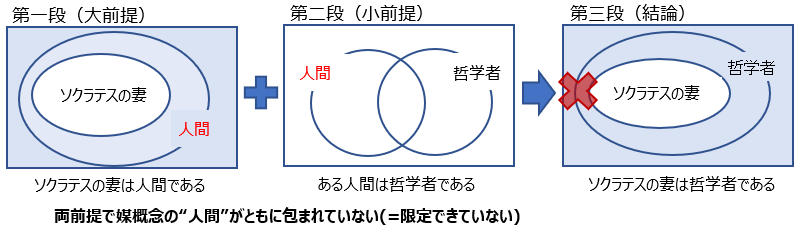
-> 結論で限定できないのはこの図の通り。この種の詭弁を「媒概念を包まない虚偽」という。
この場合、小前提で「全ての人間は・・・」とすれば成立つ
聞いていてもすっきり頭に入る。図でかけば
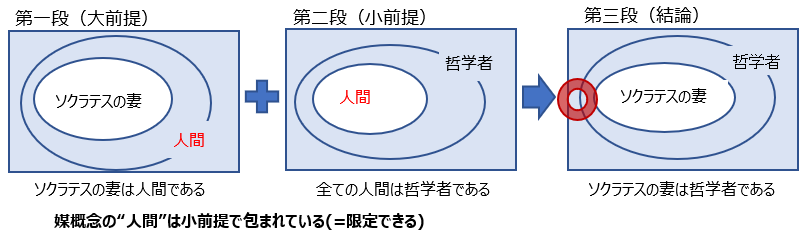
となる。
不当に包む虚偽：前提で包まれていない概念を、結論で包んではいけない。
前提で包まれていない概念を、結論で包んではいけない。このパターンも詭弁
この種の詭弁を「不当に包む虚偽」という。
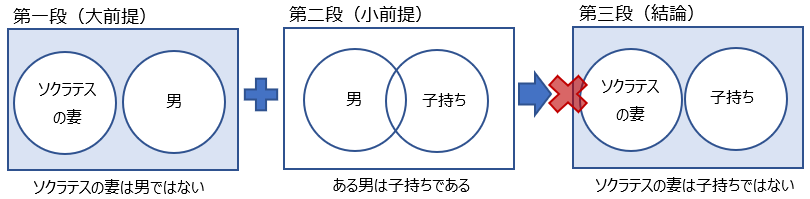
これも論理の誤りはともかくよく聞いていれば、たぶん何かおかしいと気づくかな。。
まとめ
要は、大前提、小前提の命題において、主語が”全ての～”、述語が”～でない”の概念は、”包まれている”（限定される）。この”包まれている/いない”概念は、三段論法内にて
- 媒概念は二つの前提の少なくとも一方で、包まれていなければならない。
- 二つの前提のどちらでも包まれていない概念は、結論で包んではいけない。
である事が、三段論法で正しい結論を導く規則のひとつ。
さてさて、三段論法にも色々な変形型/複合形がある。次の記事にて