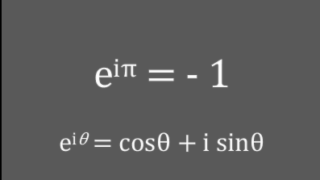オイラー大先生が対数を微分する中で、100年以上前に数学者ネイピア伯が対数研究の中で計算した式が入っている事を見つけ、ネイピア数を ”\(e \)” として 微積体系に組み込こんだ。
この ”\(e \)” を使う事により、微積の世界の繋がり具合がぐっとわかりやすくなるので覚書化。
さて、まずは対数の微分で登場する式から ”\(e \)” が定義され、そこから簡易化される対数&指数の微分の流れをつらつらと
ちなみに、”e” の定義式の解釈については、以下の覚書にて
対数の微分と \(e \) の定義
まずは” \(e \) ” を微分に結び付けた対数の微分から
対数 \( f(x) = log_a x \) の微分
\( f(x) = log_a x \) の微分 ( \( f(x) = a^x \) の逆関数)をしてみる
\( \begin{align}
f'(x) = ( log_a x )’ & = \dfrac{d}{dx} log_a x \\[6pt]
&= \displaystyle \lim_{ h \to 0 } \dfrac{log_a (x+h)- log_a x}{h} \\[6pt]
&= \displaystyle \lim_{ h \to 0 } \dfrac{1}{h} \log_a \dfrac{(x+h)}{x} = \displaystyle \lim_{ h \to 0 } \dfrac{1}{h} \log_a (1+ \dfrac{h}{x}) \\[6pt]
&= \displaystyle \lim_{ h \to 0 } \log_a (1+ \dfrac{h}{x}) ^{\frac{1}{h} } ・・・①\\[6pt]
\end{align} \)
ここで、\( t = \dfrac{h}{x} \) とすると \( h = tx \) 、\( h → 0 \) で \( t → 0 \) をふまえれば ①式は
\( \begin{align}
f'(x) = ( log_a x )’ &=\displaystyle \lim_{ h \to 0 } \log_a (1+ \dfrac{h}{x}) ^{\frac{1}{h} } \\[6pt]
& = \displaystyle \lim_{ t \to 0 } \log_a (1+ t) ^{\frac{1}{tx} } \\[6pt]
& = \displaystyle \lim_{ t \to 0 } \log_a \left\{ (1+ t) ^{\frac{1}{t} }\right\} ^{\frac{1}{x} } \\[6pt]
& = \displaystyle \dfrac{1}{x} \lim_{ t \to 0 } \log_a {\cancelto{\ e}{(1+ t) ^{\frac{1}{t}}}}・・・② \\[6pt]
(or & = \displaystyle \dfrac{1}{x} \log_a \underbrace{\lim_{ t \to 0 } (1+ t) ^{\frac{1}{t}}}_{{\color{red}e}})\\[6pt]
\end{align} \)
ここの \( t → 0 \) の \( (1+ t) ^{\frac{1}{t}} \) の式をみて、100年以上前にネイピア伯が対数研究で使用した式と関連がある事に気づいたのがオイラー大先生、 この式の極限値を”e” として微分の世界に組み込んだ。
<\(e \) の定義>
\( e = \displaystyle \lim_{ t \to 0 } (1+t)^{\frac{1}{t}}=\displaystyle \lim_{ t \to \infty } (1+\dfrac{1}{t})^{t} \)
Note: ”e”はざっくり \( e=\displaystyle (1+\dfrac{1}{∞})^{∞} \) としておけば覚えやすい(上式の両辺も同じ)
この実数 \(e \) を②式に当てはめれば、
\( \begin{align}
f'(x) = ( log_a x)’ &= \dfrac{1}{x} log_a \ {\color{red}e} ・・・③ \\[6pt]
&= \dfrac{1}{x} \dfrac{log_e e}{log_e a} \ (← 対数の底をa → e に変換)\\[6pt]
&= \dfrac{1}{x \cdot log_e a}・・・④
\end{align} \)
\( ( log_a x)’ = \dfrac{1}{x \cdot log_e a} \) ・・・④
対数 \(log_e x \ (=ln \ x) \) の微分
対数の底を \(a=e\) にとれば、式はもっと簡素になる。④式より
\( \begin{align}
( log_e x)’ &= \dfrac{1}{x \cdot log_e e} \\[6pt]
&= \dfrac{1}{x}・・・⑤
\end{align} \)
ついでに ”e” を底にした対数表示 (\(ln \)) を使っておくと( \(ln \ Z =log_e Z \) )
\( ( log_e x)’ = ( ln \ x)’ = \dfrac{1}{x}\) ・・・⑤
仕組みがわかればたいした話ではないが、最初に見た時は対数の微分が分数??と違和感大だった記憶あり。
ただ、よく使うので公式レベルで頭に入れておくとイロイロと役に立つ
指数の微分
指数 \( a^ x\) の微分
この⑤式を使えば、\( a^ x\) の微分も簡単に求まる。
\( y = a^ x\) として対数 (底 : \( e\)) を両辺にとれば
\( ln \ y = ln \ a^ x = x \cdot ln \ a\)
両辺 \( x\) で微分すれば、左辺は⑤式をつかって \( \dfrac{d(ln \ y)}{dy} \cdot \dfrac{dy}{dx} = \dfrac{1}{y} \cdot y’ \)、右辺は \( \dfrac{d(x \cdot ln \ a)}{dx}= ln \ a \) より
\( \dfrac{1}{y} \cdot y’= ln \ a \)
よって
\( y’=y \cdot ln \ a = a^ x \cdot ln \ a \)
つまり
\( (a^ x)’ = a^ x \cdot ln \ a \) ・・・⑥
となる
指数 \( e^ x\) の微分 (重要)
\(a=e\) の時、\( a^ x\) の微分は更に簡単になる。⑥式より
\( (e^ x)’ = e^ x \cdot ln \ e = e^ x \)
\( (e^ x)’ = e^ x \) ・・・⑦
関数 \( e^ x \) は 何度微分しても形はかわらない(重要)
”\( e\)” を微分で定義
さて、この指数関数にした時に微分しても形が変わらない実数を微分の定義式から ”\( e\)” として定義したのがオイラー大先生
微分前後で関数が同じある事を微分の定義式を使ってかけば、
\( \begin{align}
e^ x = (e^ x)’ &= \displaystyle \lim_{ h \to 0 } \dfrac{e^{x+ h}- e^x}{h-0} \\[6pt]
&=e^x \displaystyle \lim_{ h \to 0 } \dfrac{e^h- 1}{h}
\end{align} \)
この両辺から \(e^x \) は消えるので(\(e^x≠0 \))整理すれば、
\( \displaystyle \lim_{ h \to 0 } \dfrac{e^h- 1}{h} = 1\) ・・・⑧
この微分から導いた⑧式を満たす実数を ”\( e\)” としたのがオイラー大先生。
⑧式にたどり着いた元は、上の対数の微分で
\( e = \displaystyle \lim_{ t \to 0 } (1+t)^{\frac{1}{t}}=\displaystyle \lim_{ t \to \infty } (1+\dfrac{1}{t})^{t} \)
としたこと。
また、 \( e\) の指数関数 \( e^ x \) にした時に何度微分しても形が変化しないこの性質は、様々なトコロで大活躍。
オイラーの定理(\( e^{iθ}=cosθ+i\cdot sinθ \)) にもつながる
追記
\( e^x\) と \( ln \ x\) の図示 ( \(y=x \) 対象 )
\( e^x\) の微分は \( e^x\)のまま、\( ln \ x\) の微分は \(\dfrac{1}{x}\) と、この2つの曲線の動きに関連なさげ感のイメージ、逆関数である事はわかるのであるが、そのイメージがつかみづらかった記憶があるので一応図にかいて認識 & 覚書化。
当たり前だが、\(y=x \) でちゃんと対象。
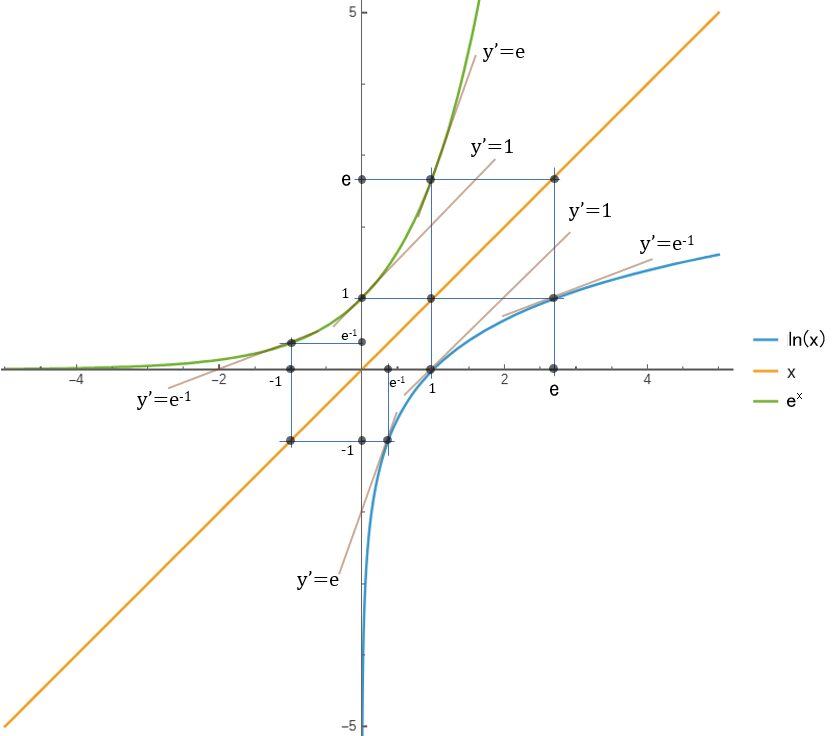
それぞれの微分値も ”\( y=x\)” にて対象。
\( \displaystyle \lim_{ x \to 0 } \dfrac{ln \ (1+x)}{x} = 1 \) の求め方
\(e^x \) の導入に使うので、 \( \displaystyle \lim_{ x \to 0 } \dfrac{ln \ (1+x)}{x} = 1 \) の求め方もついでに
上の ”\( ln \ x \) の微分” と ”平均値定理”を使用する。
<平均値の定理>
\(f(x)\) が 区間 \( [a,b] \)で連続で微分可能な関数であるとき
\( f'(s) = \dfrac{f(b)-f(a)}{b-a} \)
となる \(s\) が、\(a\) と \(b\) の間に存在する。
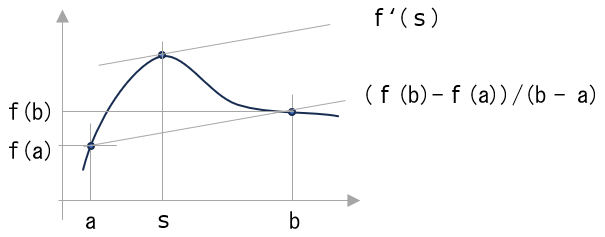
(\( a → 1, b → (1+x) \) に書き換えて )
関数 \( f(x)= ln \ x \) に平均値定理を使えば、\(1\ ~ \ (1+x) \) の間に \( s \) が
\( \dfrac{ln \ (1+x) – \ ln \ 1}{(1+x)-1} = f’ (s) \)
にて存在する。
さて、ここで\(ln \ 1 = 0 \) である事、 また \( f’ (x)= (ln \ x)’= \dfrac{1}{x}\) より \( f’ (s)=\dfrac{1}{s} \) である事を使えば、
\( \begin{align}
\dfrac{ln \ (1+x) – ln \ 1}{(1+x)-1} &=\dfrac{ln \ (1+x)}{x}\\[6pt]
&= \dfrac{1}{s} \ (= f’ (s))
\end{align} \)
\(s \) は \(1~x \) の間にある事から (\(1< s <x \))、 \( x → 0 \) に伴い \(s\) は \( s → 1 \) に落ちる。
\( f(x)’= \displaystyle \lim_{ x \to 0 } \dfrac{ln \ (1+x)}{x} = \displaystyle \lim_{ s \to 1 }\dfrac{1}{s} = 1 \)
よって、
\( \displaystyle \lim_{ x \to 0 } \dfrac{ln \ (1+x)}{x} = 1 \) ・・・⑨
\(e^x \) の導入についての覚書は
以上