はじめに
”e =2.718281828・・・” (ネイピア数、自然対数の底)の定義は
\( e=\displaystyle \lim_{ n \to \infty } (1+\dfrac{1}{n})^{n} \) ・・・①
円周率\(\pi \) であれば、直径に対する円の全周長を比で表したのが \(\pi = 3.1415・・・ \) とかの説明で十分、特にひっかかりなし。
だが、この ”\(e \)” については、ん?一言でいうと何だ? 、あれ、そもそもこの定義の式の意味って、、、なんだっけ?? と。。。
で、覚書化
\(e \) の定義式の仕組み
\(e \) が意味するトコロより前に(特別な値(超越数とか)とされている背景等)、まずは定義式の意味するところがわからないと始まらないので、まずは式の解釈から。。
先に書いておくと、\(e^x \) は
\(e^x =\displaystyle \lim_{ n \to \infty } (1+\dfrac{x}{n})^{n} \) ・・・②
であり、複利計算の式
\(S_{n} =a \cdot (1 + \dfrac{r}{n})^n \) ・・・③
( 期間 \(T\) で 利率 \(r\times 100 \)(%)、期間T内での清算回数 \(n \) )
の清算回数を \(n → ∞\)、\( a=1 \) とした時の式と一致する。
また、\(e \) は ②式が \(x=1 \) のとき
\( e=\displaystyle \lim_{ n \to \infty } (1+\dfrac{1}{n})^{n} \) ・・・④
同様に、\( \dfrac{1}{e} \) は、②式が \(x=-1 \) のとき
\( \dfrac{1}{e}=\displaystyle \lim_{ n \to \infty } (1-\dfrac{1}{n})^{n} \) ・・・⑤
である。
さて、複利計算の意味をふまえ先にまとめておくと、
\(e \) のとらえ方としては、
- 値の初期値を ”1”として、期間 T で2倍にふやす増加力が常時作用する環境下(率:100%)
- Tの期間中、値は常時増加し、増加した分もその増加に組み込まれながら全体が増加する仕組み
の条件下では、期間 T 経過時、2倍ではなく \(e = 2.71828・・・\) 倍になる 。← e はこの環境下 ”実増加率” の意味をもつ
(初期値”1”なので ”率” としておく)
同様に \(\dfrac{1}{e} \) は、期間 T で\(\dfrac{1}{2} \)倍となる減少力がかかる環境下において、 ”実減少率” が \(\dfrac{1}{e} = \dfrac{1}{2.71828・・・}\) であることを示す。
と見ることができる。
\(e \) と複利計算の式の仕組みがつながれば \(e\) のイメージもしやすいのだが、この 複利計算の式の仕組み (\(e \)の定義式) 自体がとっつきにくい
(1に1/nを足して、それをn乗してから無限大に飛ばす?ん?と)
この仕組みを理解するには、まずは複利計算のやり方の理解から入るのが手っ取りばやい。
で、シンプルな単利計算から
→ 複利計算式の仕組みが大丈夫であれば、一気にとばして”e の定義式”へ
単利計算の式
清算回数:期間中1回清算
ここは簡単。
満期額の計算は、
満期金額=元金+利子=元金+(利率x元金)
=元金・(1+利率)
元金を\(a \)、利率を \(r\times 100 \)(%)、利率の期間を\(T\)、期間 \(T\) 後の満期金額を \(S_{1(1)} \) とすれば、
\(S_{1(1)} = a + a \cdot r= a \cdot (1 + r) \) ・・・⑥
図にかけば、こんな感じ(当然、とてもシンプル)

当たり前だが、元金 \(a \) に \( (1 + r)\) を掛ければ 満期額 \(S_{1(1)} \) 。
別の見方をすれば、\( (1 + r) \) は、元金 \(a \) に対する実増加率。
(<-複利計算はこの構造の繰り返し(同じ構造の式が組み込まれていく)、それが \(e \) の意味の理解につながるので一応。。。)。
複利計算の式
さて、複利計算へ。
清算回数:期間中2回清算
同じ利率 \(r\times 100 \)(%)で期間 \(T\) も同じ。
ただし、半分の \(\dfrac{1}{2} \)T の期間経過時に、一度利子を清算 (預金額: \(S_{2(1)}\) )
次の期間はこの利子を加えた額 \(S_{2(1)}\) を加え、元金を増やして再度預金、満期時(期間\(T\) 経過時)に清算。
この満期時の預金額 \(S_{2(2)} \) を以下で計算する(複利計算)。
さて、一回目の清算時の預金額は同じ式構成だが、期間は \(\dfrac{1}{2} \)T 分となるため 利子は \( a\times \dfrac{r}{2} \)
よって、
\(S_{2(1)}= a (1 + \dfrac{r}{2})\) ・・・⑦
↑これが二回目の期間の元金。
満期時の預金額\(S_{2(2)} \) は⑦を元金として、
\(\begin{align}
S_{2(2)} &= a \cdot (1 + \dfrac{r}{2})+ a \cdot (1 + \dfrac{r}{2}) ・\dfrac{r}{2} \\[6pt]
&= a \cdot (1 + \dfrac{r}{2})^2 ・・・⑧
\end{align} \)
となる。
式を見るより、図で見た方が構造はわかりやすいかも。図に描くとこんな感じ
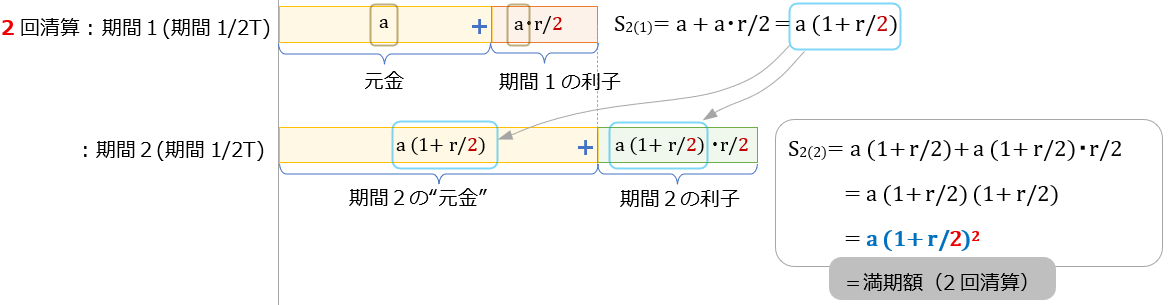
単利の時と同様④式の \( (1 + \dfrac{r}{2})^2 \) の部分は実増加率、元金\(a \)に対して何倍になるか?の係数。
(\( S_{2(2)} = a \times (実増加率) \)) ← この構造は1回清算の時と同じ
清算回数:期間中3回清算
もう少し流れをはっきりさせるのに、3回清算も図にかいておく。
満期時の預金額は、
\(S_{3(3)}\) は、\(S_{3(3)} =a \cdot (1 + \dfrac{r}{3})^3 \) ・・・⑨
となる。
各清算回の式を、図に描けばこんな感じ 。
\( (1 + \dfrac{r}{3})^3 \) が組み込まれていく様子がわかる。
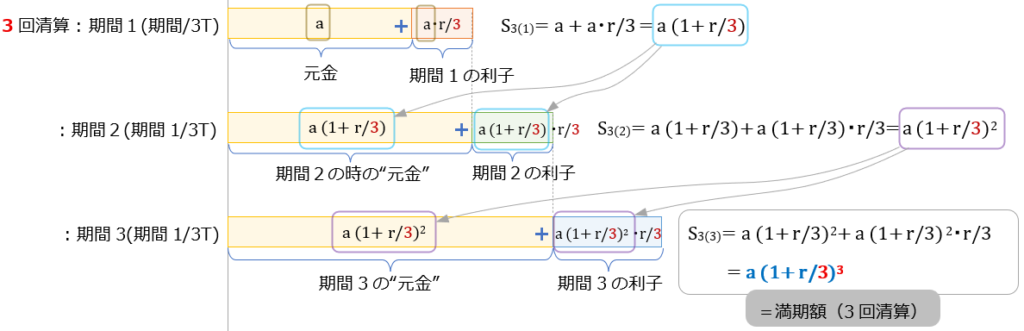
今までの計算と同様に、⑨式の \( (1 + \dfrac{r}{3})^3 \) の部分は、元金\(a \)に対して何倍になるか?の実増加率を示す係数
( \( S_{3(3)} = a \times (実増加率) \)) ← この構造は2回清算の時と同じ
清算回数:期間中n回清算
さて、清算回数がn回になった場合を計算してみる
数列を使ってもよいし帰納法で証明しても良いが、上と同じように \( (1 + \dfrac{r}{n}) \) が組み込まれていくだけなので、ここでは以下の図で十分。
で、組み込まれる様子見ながら満期時の預金額 \(S_{n(n)} \) を下の図から算出
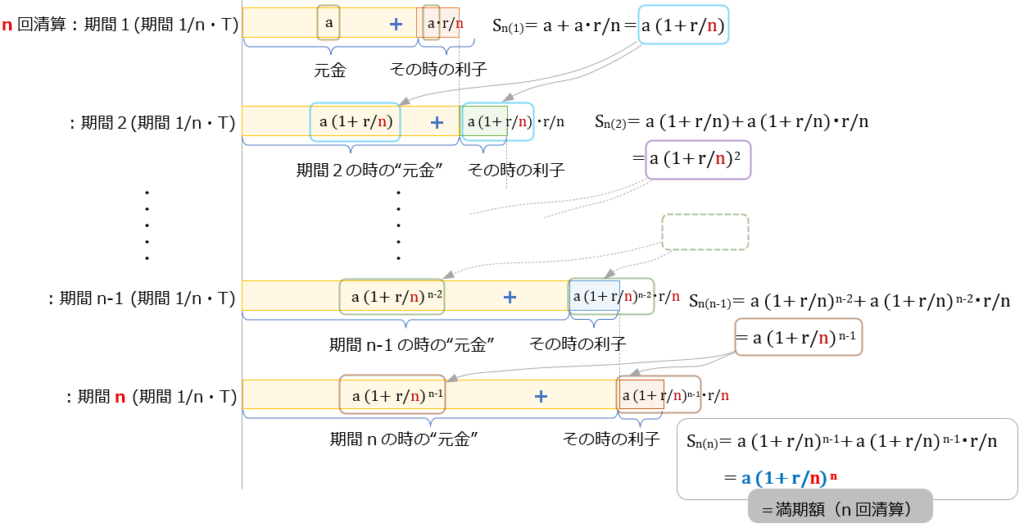
満期時の預金額は、
\(S_{n(n)} =a \cdot (1 + \dfrac{r}{n})^n \) ・・・⑩
ここでも、この⑩式の \( (1 + \dfrac{r}{n})^n \) は、元金\(a \) が満期時に何倍になるかの”実増加率” になっている
( \( S_{n(n)} = a \times (実増加率) \) ) ← この構造は同じまま
以上が、利子が元金が組み込まれていく時の式の仕組み(構造)
清算回数:期間中に∞回清算
さて、⑩式をつかって清算回数を無限大にすれば、単純に
\(S_∞ =\displaystyle \lim_{ n \to \infty } a \cdot (1 + \dfrac{r}{n})^n \) ・・・⑪
( \( S_∞ = a \times (実増加率) \) ) ← 結局、最後までこの構造は変わらない
結局、( \({\color{green}{1}} + \dfrac{r}{n}\) ) は、” その清算回の元本率(\(\color{green}{1}\)) ” + ” \(\color{blue}{n}\) 回清算時の一回当たりの利率 (\(\dfrac{r}{\color{blue}{n}}\)) ” であり、とどのつまりが、清算一回当たりの元本の増加率。
ある回の清算時の預金額は、(前の回までに増えた)元本に”同率”の ( \({\color{green}{1}} + \dfrac{r}{n}\) ) をかければ、その回の預金額が算出される構造。
( \( \underbrace{S_(x)}_{x回清算時の預金額} =(\underbrace{a \cdot ( 1 + \dfrac{r}{n})^{x-1} }_{前の回((x-1)回目)からの元本}) \cdot (\underbrace{1 + \dfrac{r}{n}}_{一回当たりの増加率}) \))
満期の時は、この掛け算を \(\color{red}{n}\) 回繰り返す事になるため、実増加率は単純にこれを(\(\color{red}{n}\)乗) すればよい。つまり、実増加率は、 ( \(1 + \dfrac{r}{n})^ {\color{red}{n}} \)
これがこの式のしくみ( 初期値(元金)の \(a \) を掛ければ満期時の預金額が算出される)
で、この清算回数の \(n\) を無限大にとばしたのが⑦式
e の定義式
さて、ここまでくれば既に \(e \) の定義式は既にみえてはいるが、一応。
⑪式にて
- 元金 \(a =1 \)
- 利率 \(r=1\) (100%:期間Tで2倍)
とすれば、 \(e \) の式と一致
つまり、⑪式の満期時の預金額 \(S_{\infty}\) が
\(S_{\infty}=\displaystyle \lim_{ n \to \infty } (1+\dfrac{1}{n})^{n} =e \) ・・・⑫
となり、”\(e \) ”の定義式と一致。
\(e \) の定義式は、複利計算式の限定版
また、これを計算すれば、\(S_{\infty}=e = 2.71828・・・ \) となる
(⑫式が収束する事、値の算出はまた別途)。
以上が、”\(e \) ”の定義式からの意味の解釈
注記:
\(e \) の定義式内では、同じ ”1” であるが故に ”初期値” と ”利率” は見えにくくなっているが、
\( \begin{align}
e &=\displaystyle \lim_{ n \to \infty } (1+\dfrac{1}{n})^{n} \\[6pt]
&= 1(:初期値) \times \displaystyle \lim_{ n \to \infty }(1+\dfrac{1(:利率)}{n})^{n}
\end{align}\)
を各々意味している。
↑ ”1” である箇所が複数あるが、それぞれの”1”にも別の意味がある
以下 \(e \) の定義式 からの解釈のまとめ(冒頭とほぼ同じ)
- 値の初期値を ”1”として、期間 T で2倍にふやす増加力が常時作用する環境下(率:100%)
- Tの期間中、値は常時増加し、増加した分もその増加に組み込まれながら全体が増加する仕組み
の条件下では、期間 T 経過時、2倍ではなく \(e = 2.71828・・・\) 倍になる 。。← e はこの環境下 ”実増加率” の意味をもつ
(初期値”1”なので率)
単純例:100万円を年利100%(一年(期間T)で2倍)で運用したとすると、単利(一回清算)だと一年後に200万円。
同じ年利でも頑張って毎日毎時間毎秒でも清算し続け増えた利子分をどんどん元金に組み込んでいけば、一年後には倍の200万円ではなく、約271.8万円(=100万円x\(e \) )に近い額まで届くって話。
これで捉えておくと、”\(e \) ” も少し身近。
ここでの肝は、増加した分も増加に組み込まれながら全体が増加する仕組み を意味する ” \(a \cdot (1 + \dfrac{r}{n})^n \) ”(の構造)が入っている事
→ ここを抑えれば、”\(e \) ” の定義式は単に複利計算の限定版(利率100%、初期値1)。なんて事なし。。。
追記
要は、増加した分も増加に組み込まれながら全体が増加する仕組みのモト、初期値を ”1” 、期間 Tで ”2倍” になる増加力が作用する環境下での実増加率が ”e”、って事。
こうしてみると見ると、色々なトコロで”e”が出てくるのは、結構自然に思えてくる(イメージしやすくなる)。
(一年したら急に倍になるっていうより、徐々に増加していく方が普通、増えた分も次の増加に組み込まれて寄与していくのも普通。。。)
ちなみに、
\(e^x =\displaystyle \lim_{ n \to \infty } (1+\dfrac{x}{n})^{n} \)・・・②
であるが、上述の⑫式 \(S_∞ =\displaystyle \lim_{ n \to \infty } a \cdot (1 + \dfrac{r}{n})^n \) と比較すれば、関数 \(e^x \) の ”\( x \) ” はその環境下での増加力として働き(⑦式での利率”\( r\) ”)、\(e^x \) は、増加力が変化していく時の出力値であるとみる事ができる。
\(e^x \) の導入ついてはこちら
ついでに ”\( x \) ” の増加にともなう関数 \(e^x \) の見方として、たとえば \( x =1、2 \) を例にとれば、
- \( x =1 \) : \(e^{\color{red}{1}}\)
→ <解釈> 期間Tで2倍になる一定の増加力( \(\color{red}{1} \) = 100%(利率)) がかかる環境下では、期間T経過時の実増加率は約2.718倍 (= \(e^1 \)) になる - \( x =2 \) : \(e^{\color{red}{2}}\)
→ <解釈> 期間Tで3倍になる一定の増加力( \(\color{red}{2} \) = 200%(利率)) がかかる環境下では、期間T経過時の実増加率は約7.389倍 (= \(e^2 \)) になる - ・・・
といった見方も可。
(\( x \) が時間tで表してある関数といった例 ( \(e^{αt}\))であれば、時間tの経過に伴い ”増加力(利率)自体が増える環境下” での関数、とイメージするのもいける)
最後に、”\(e \)” の値の語呂合わせ
”\(e \)” の値の語呂合わせ:
e =2.71828182845904523536・・・
(フナ一鉢二鉢しごく押し目にさめ山麓:め=5)

