はじめに
三角関数の加法定理
- \( sin(α+β)=sinα \cdot cosβ + cosα \cdot sinβ \) ・・・(1)
- \( sin(α-β)=sinα \cdot cosβ – cosα \cdot sinβ \) ・・・(2)
- \( cos(α+β)=cosα \cdot cosβ – sinα \cdot sinβ \) ・・・(3)
- \( cos(α-β)=cosα \cdot cosβ + sinα \cdot sinβ \) ・・・(4)
これらは、オイラーの公式からも導く事ができるが(記事↓)
今回は、この加法定理を”図”で理解したときの覚書。
-> ベクトルの内積をつかえば(+図解すれば)簡単に仕組みがわかる
ベース知識:ベクトルの内積 (以下抜粋)
<内積の定義> \( \vec{a}\) と \( \vec{b} \) の二つのベクトルのなす角が α の時の内積定義 : \( \vec{a} \cdot \vec{b} = | \vec{a} | \cdot | \vec{b}| \cdot cos(α)\)
<内積の成分計算> 二つのベクトルの成分 \( \vec{a}
=\left ( \begin{array}{c}
a_x\\
a_y \end{array} \right ) \) 、\( \vec{b}
=\left ( \begin{array}{c}
b_x\\
b_y \end{array} \right ) \) を使用した内積計算: \( \vec{a} \cdot \vec{b} =a_x \cdot b_x+a_y \cdot b_y \)
上記の(1)~(4)の加法定理の式のうち、(内積計算とリンクしやすいように、)まずは(4)式の \( cos(α-β)=cosα \cdot cosβ + sinα \cdot sinβ \) からとりかかる。
まずは、cos(α-β)=cosα・cosβ + sinα・sinβ ・・・(4) から
この (4)式 の右辺をよーくみてみると、単純な ベクトルの内積の成分計算である事に気づく
つまり右辺は、\( \vec{a}
=\left ( \begin{array}{c}
cos α\\
sin α \end{array} \right ) \) 、\( \vec{b}
=\left ( \begin{array}{c}
cos β\\
sin β \end{array} \right ) \) とした時の、\( \vec{a}\) と \( \vec{b}\) の内積の成分計算
\( \vec{a} \cdot \vec{b} = cosα \cdot cosβ + sinα \cdot sinβ \) ・・・(5)
である。
次に、この二つのベクトルのなす角が(αーβ)である事を使い(下図参照)、
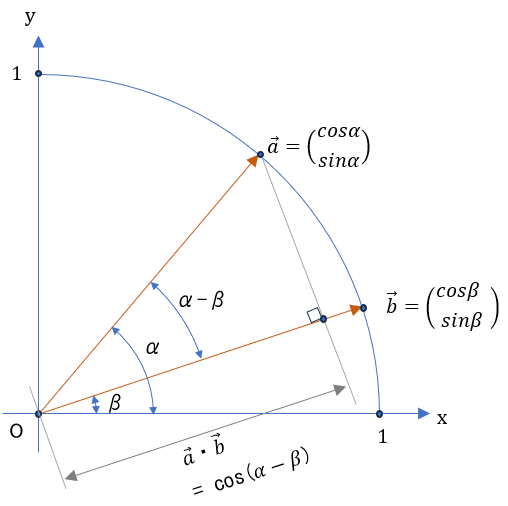
ベクトルの内積の定義の式に入れれば、
\( \vec{a} \cdot \vec{b} = | \vec{a} | \cdot | \vec{b}| \cdot cos(αーβ) \) 。
また、\( | \vec{a} | =| \vec{b}| =1 \) より
\( \vec{a} \cdot \vec{b} = cos(αーβ) \) ・・・(6)
で、今度は左辺が出てくる。(5)(6)式をまとめれば
\( \vec{a} \cdot \vec{b} = cos(αーβ) = cosα \cdot cosβ + sinα \cdot sinβ \) <— 加法定理の (4)式が出る
とどのつまり(4)式は、”内積の定義の式” (左辺)と”内積の成分計算の式” (右辺) を抜き出して書いているだけ
ベースは\( \vec{a}\) の \( \vec{b} \) への投影長。これは、内積の意味=投影長 である事を思い出せば、そりゃそうか、、にしかならない。。。
ちなみに、内積の成分計算の導き方についてはこちらが覚書(よく忘れるので。。。)↓
つづいて、\( sin(α-β) \) を見てみる
つづいて sin(α-β)=sinα cosβ – cosα sinβ ・・・(2)
見やすくするのに、(2)式の右辺を少しいじって、
\( \begin{align}
sin(α-β) &=sinα \cdot \cos β \ \ – \cos α \cdot sinβ \\[8pt]
& = cosα \cdot (-sinβ) + sinα \cdot cosβ
\end{align} \)
とすれば、\( cos(α-β) \) の時と同様に \( \vec{a}
=\left ( \begin{array}{c}
cos α\\
sin α \end{array} \right ) \) と \( \vec{c}
=\left ( \begin{array}{c}
– sin β\\
cos β \end{array} \right ) \) の二つのベクトルの内積の成分計算である事がわかる。
つまり、
\( \vec{a} \cdot \vec{c} = sinα \cdot \cos β \ \ – \cos α \cdot sinβ \) ・・・(7)
次に、\( \vec{b} \) と \( \vec{c} \) が直行している事(∵ \( \vec{b} \cdot \vec{c} =0 \) ) を使えば 、\( \vec{a} \) と \( \vec{c} \) のなす角は (\( \dfrac{\pi}{2} – (αーβ) \))。
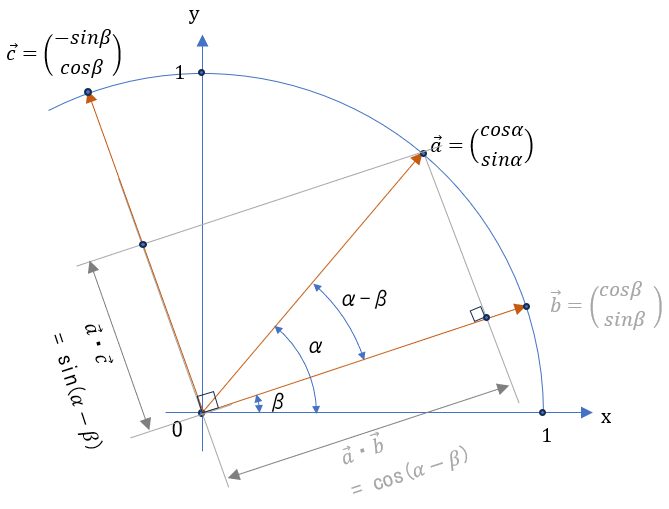
よって、ベクトルの内積は、
\( \vec{a} \cdot \vec{c} = | \vec{a} | \cdot | \vec{c}| \cdot cos(\dfrac{\pi}{2}-(αーβ)) \)
これに、\( | \vec{a} | =| \vec{c}| =1 \)、\( cos(\dfrac{\pi}{2}-(αーβ)) = sin(αーβ) \) をふまえれば、
\( \vec{a} \cdot \vec{c} = sin(αーβ) \) ・・・(8)
(7)(8)式をまとめて
\( \vec{a} \cdot \vec{c} = sin(αーβ) = sinα \cdot \cos β \ \ – \cos α \cdot sinβ \) <— 加法定理の (2)式が出る
残りの cos(α+β) = cosα cosβ – sinα sinβ も sin(α+β) = sinα cosβ + cosα sinβ も 同じ
残りの
- \( sin(α+β)=sinα \cdot cosβ + cosα \cdot sinβ \) ・・・(1)
- \( cos(α+β)=cosα \cdot cosβ – sinα \cdot sinβ \) ・・・(3)
は、(2)(4)式のβに(-β)をに代入すれば、式変形だけで(1)(3)式がそのまま出てくるが、一応こちらも図解で。。。
(4)式を(3)式にするには、( 単純に \( α-(-β) = (α+β) \) から) (4)式の β の正負を逆方向(-β)にしてやればよい。
(4)式の \( \vec{b} \) の β の正負を逆方向(-β)とした \( \vec{d}
=\left ( \begin{array}{c}
cos (-β)\\
sin (-β) \end{array} \right ) =\left ( \begin{array}{c}
cos β\\
-sin β \end{array} \right )\) をつかい、これを図に反映すれば、
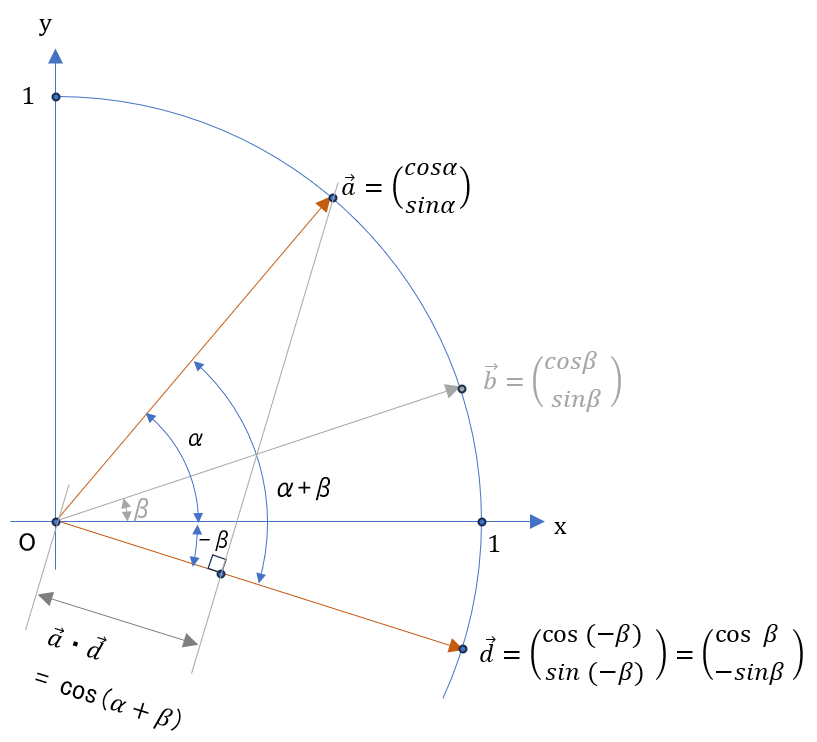
\( \vec{a} \) と \( \vec{d} \) の内積計算すれば
\( \vec{a} \cdot \vec{d} = cos(α+β) = cosα \cdot cosβ – sinα \cdot sinβ \) <— 加法定理の (3)式が出る
(1)式は、\( \vec{e} \) を\(\vec{d} \) に直交にとれば、\( \vec{e}
=\left ( \begin{array}{c}
sin β\\
cos β \end{array} \right ) \) 。
これを図に反映して
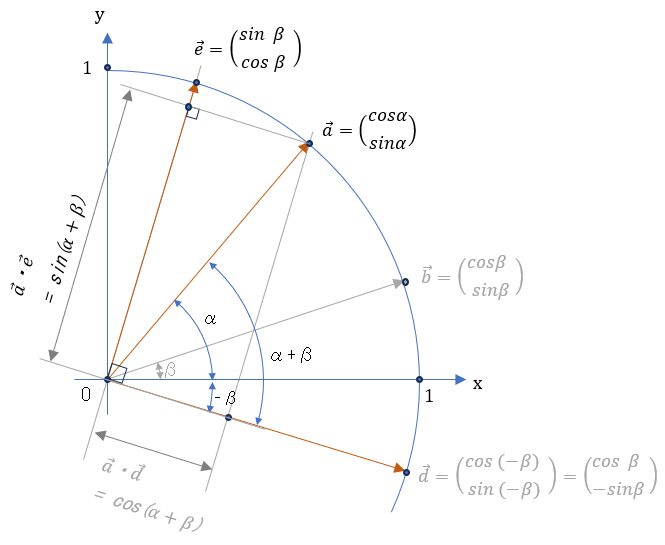
\( \vec{a} \) と \( \vec{e} \) の内積計算すれば
\( \vec{a} \cdot \vec{e} = sin(α+β) = sin α \cdot cosβ + sinα \cdot cosβ \) <— 加法定理の (1)式が出る
最後に
三角関数の加法定理とベクトルの内積の関係の覚書。図にかけば理解しやすい。
ちなみに、\( a \cdot cos x + b \cdot sinx \) の型の三角関数は、\( \sqrt{a^2+b^2} \cdot cos(x - θ ) \) の形に”常に”変形できるが、これもほぼ同じ(ひと工夫加えて、ベクトルの内積としてみながら加法定理としてみれば同じ。)
こちらに覚書