はじめに
\(sin x \) と \(cos x \)のたし算 / ひき算について。つまり、\( a \cdot cos x ± b \cdot sinx \) の型。この型は、\( \sqrt{a^2+b^2} \cdot cos(x ̠∓ θ ) \) の形に、”常に“変形できる。
↑(sinとcosを一つまとめられるので)知ってると意外と役にたつ
例えば、\( y = \sqrt{3}cos x + sinx \) であれば、\( y = 2 cos(x ̠- \dfrac{\pi}{6} ) \)
暗算としてはこんな感じ
辺 \( {1}:{2}:\sqrt{3} \) の直角三角形を頭の中に浮かべる (斜辺 : \( 2^2= \sqrt{3}^2+1^2 \) )
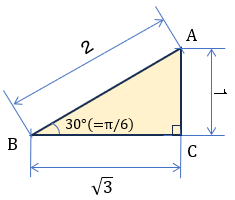
↑この三角形 ( ∠ABCが θ で、この場合 θ=30°= \(\dfrac{\pi}{6}\))
この三角形から、斜辺AB=2と \( θ=\dfrac{\pi}{6}\) を使って、 \( \sqrt{3}cos x + sinx = {\color{red}2} \cdot cos(x ̠- {\color{red}\dfrac{\pi}{6}} ) \) となる。
仕組みは、単に三角関数の加法定理にひと手間加えているだけなので、見方としては下の記事と同じ
まずはたし算から
\(a・cos x + b・sinx \) の型のたし算
\(cos x \) と \(sin x \) のたし算の前に、まず係数の \( a \) 、\( b \) の見方から。
BCの線分長を \( a \) 、CAの線分長を \( b \)にとり、斜辺AB \( {\sqrt{a^2+b^2}} \) とした直角三角形ABCの∠ABC=θとする。 (下図参照)。
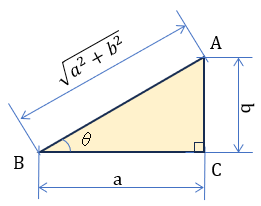
この時、\( \overrightarrow{BA} = \vec{m}=\left ( \begin{array}{c}
a \\
b \end{array} \right ) \) とすれば \( \vec{m}= \left ( \begin{array}{c}
a \\
b \end{array} \right ) = {\sqrt{a^2+b^2}} \left ( \begin{array}{c}
cos θ\\
sin θ \end{array} \right )\) (← 単に極座標表示化しただけ)
ここで、任意の”単位”ベクトル \( \vec{n} \) を \( \vec{n}
=\left ( \begin{array}{c}
cos x\\
sin x \end{array} \right ) \) と設定すれば、 \( \vec{m} \)、\( \vec{n} \) の内積は、
\( \begin{align}
\vec{m}\cdot \vec{n}&= \left ( \begin{array}{c}
a \\
b \end{array} \right ) \cdot \left ( \begin{array}{c}
cos x\\
sin x \end{array} \right ) \\[6pt]
&={\sqrt{a^2+b^2}} \left ( \begin{array}{c}
cos θ\\
sin θ \end{array} \right ) \cdot \left ( \begin{array}{c}
cos x\\
sin x \end{array} \right ) \\[6pt]
&={\sqrt{a^2+b^2}} \cdot (cos θ\cdot cosx + sin θ \cdot sinx) <-ここで加法定理を使い\\[6pt]
&= {\sqrt{a^2+b^2}} \cdot cos(x-θ)
\end{align} \)
図にかけばこんな感じ
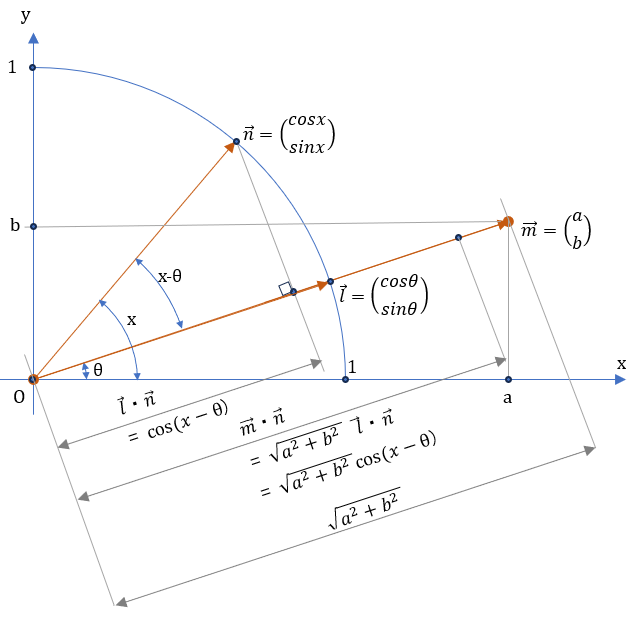
\( \vec{m}\cdot \vec{n} = a\cdot cosx + b \cdot sinx \) を踏まえれば、この式展開の一行目と四行目が求める式。つまり、
\( \vec{m}\cdot \vec{n} = a\cdot cosx + b \cdot sinx= {\sqrt{a^2+b^2}} \cdot cos(x-θ) \) ・・・①
とどのつまりこの足し算 \( a \cdot cos x + b \cdot sinx \) は、\( \vec{m} \) と \( \vec{n} \) の内積の成分計算式。
これを一旦、” \( \vec{n} \) “と” \( \vec{m} \) の単位ベクトル “の内積と見る事で加法定理を使い、あとから \( {\sqrt{a^2+b^2}} \) 倍して (\(\overrightarrow{BA} \) の大きさ分元に戻して)いるだけ。
\( a・cos x \ \ – \ \ b・sinx \) の型のひき算
つづいて、\(cos x \) と \(sin x \) のひき算、つまり\( a \cdot cos x – b \cdot sinx = a \cdot cos x +(- b) \cdot sinx\) とみれば、たし算と同じ。
\( a \) と \( b \) の見方、θは同じ。\(\overrightarrow{BA} \) とは逆回転の( \( -β \) 方向)ベクトルを \( \vec{k} \) とする。
\( \vec{k} \) は 、\( \vec{k} =\left ( \begin{array}{c}
a \\
-b \end{array} \right ) = {\sqrt{a^2+b^2}} \left ( \begin{array}{c}
cos θ\\
-sin θ \end{array} \right )\) となり、 \( \vec{n} \) はたし算の時と同じ単位ベクトル \( \vec{n}
=\left ( \begin{array}{c}
cos x\\
sin x \end{array} \right ) \) を使い内積を計算すれば、
\( \begin{align}
\vec{k} \cdot \vec{n} &= a\cdot cosx – b \cdot sinx \\[6pt]
&={\sqrt{a^2+b^2}} \cdot (cos θ\cdot cosx – sin θ \cdot sinx) <-ここで加法定理を使い\\[6pt]
&= {\sqrt{a^2+b^2}} \cdot cos(x+θ)
\end{align} \)
この式展開から、
\( a\cdot cosx – b \cdot sinx= {\sqrt{a^2+b^2}} \cdot cos(x+θ) \) ・・・②
が確認できる。図に書けばこんな感じ
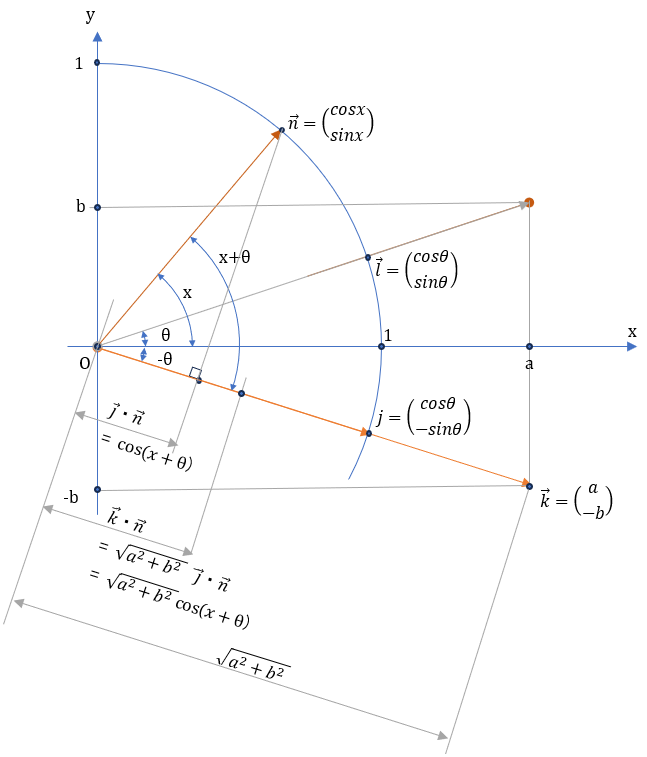
さいごに
\( sin(x ̠± θ ) \)に落としたい時は、a.bを入れ替えて \( θ → θ+\dfrac{\pi}{2} \) と見てやれば同じ計算。
つまりこの三角形
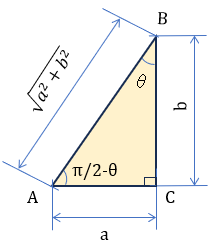
\( cos(\dfrac{\pi}{2} – θ) = sinθ \)、\( sin(\dfrac{\pi}{2} – θ) = cosθ \) をふまえれば、
\( \begin{eqnarray} a = \sqrt{a^2+b^2} \cdot cos( \dfrac{\pi}{2} – θ) = \sqrt{a^2+b^2} \cdot sinθ \\[6pt]
b = \sqrt{a^2+b^2} \cdot sin(\dfrac{\pi}{2} – θ)= \sqrt{a^2+b^2} \cdot cosθ
\end{eqnarray} \)
より、
\( \begin{align}
a\cdot cosx + b \cdot sinx &= \sqrt{a^2+b^2} \cdot (sinθ \cdot cosx + cosθ \cdot sinx) \\[6pt]
& = \sqrt{a^2+b^2} \cdot sin(x+θ)
\end{align} \)
の式展開から出てくる。\( sin(x ̠- θ ) \) も同じ三角形を使えば、cosの時と同じ。
以上

