はじめに
前回の記事はねじの概要(ねじの強度区分、入力トルクと軸力の関係)。
今回は、入力トルクの設定方法と管理方法について
今回もこの二冊がベース
”ねじ締結の原理と設計”と”ねじ締結概論”。
ねじの締結の管理方法
さて、締付け管理方法として代表的なものは以下3種類
- トルク法
- 規格降伏点以下の弾性域にて軸力確保を行う締付けトルク管理方法。
- 弾性域での締結管理
- 回転角法
- トルク入力の安定点(スナグトルク)から降伏点~極大値間に至るレンチの入力角度を予め設定し、その規定回転角を締結時に入力する事により軸力確保する締付けトルク管理方法
- 塑性域での締結管理
- トルク勾配法
- 締付け回転角に対する締付けトルクの勾配の低下を確認した時点でトルク入力を停止する事により塑性域入り口での軸力確保をするトルク管理方法
- 塑性域での締結管理
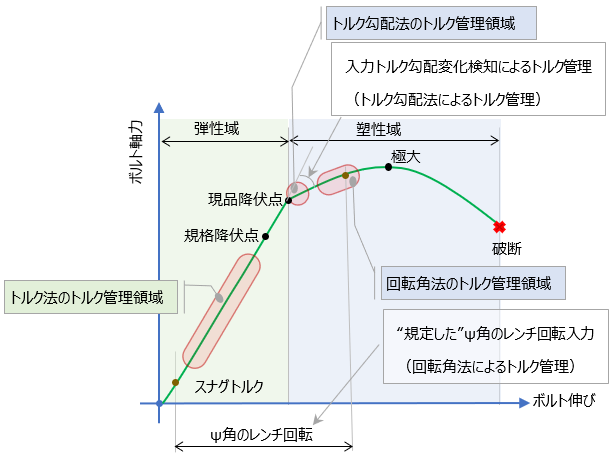
塑性域までのトルク入力を要する”2. 回転角法”と”3.トルク勾配法” は、高軸力が期待できるがボルトは塑性変形をおこすので当然ボルトの再利用不可(締結毎の交換が前提)。
メンテ/組バラシを前提とする部品等、同じボルトを複数回使用する事を前提する場合は、トルク法にて締付け管理が行われる。
入力トルクの設定(理論値):ボルトの弾性域内での管理
さてトルク法における入力トルク Tf の設定計算。
ねじの弾性域内で管理するため、Tf はおねじ材料の降伏点を限界として軸に入力できる最大応力σHから求める。
軸にかかるトルクTsと軸の応力
まず、ねじに入力されたトルク Tf の分解。トルク入力時 Tf は、
- ボルト座面に作用するトルク(b):Tw
- ねじ部に作用するトルク(a):Ts
として作用し、その関係は Tf = Tw + Ts (締結の仕組み概要 も参照)
この式のトルクTsを使う。こちらの記事からTsは、
\(\tt T_s= \displaystyle{ \frac{F_s}{2}(\frac{P}{\pi}+\frac{\mu_s \cdot d_p}{\cos\alpha})} \)・・・①
(発生軸力: Fs ねじピッチ:P、 ねじの有効径:dp 、ねじ面の摩擦係数:μs 、ねじの山の半角:α)
さて、トルクが入力されるとボルト軸部には
- ボルトの伸びから発生する引張応力:\(\tt \sigma =\displaystyle \frac{4F_s}{\pi\cdot d_s^2} \\[8pt] \)
- ボルトのねじりから発生するせん断応力:\(\tt \tau = \displaystyle \frac{16T_s}{\pi\cdot d_s^3} \)
が発生している。ds: \(\tt d_s=\displaystyle \frac{d_2+d_3}{2} \) ( d2:おねじ有効径、d3:おねじ有効断面積ASの径 )
ここで、σとτの比をもとめれば \( \tt \displaystyle \frac{\tau}{\sigma} = \displaystyle \frac{4T_s}{F_s\cdot d_s} \)、これに①式を代入すれば、
\( \tt \displaystyle \frac{\tau}{\sigma} = \displaystyle \frac{2}{d_s} (\frac{P}{\pi}+\frac{\mu_s \cdot d_p}{\cos\alpha}) \) ・・・②
となる。
(この先の簡易表記のため)ついでに②式の右辺を
\( \tt\kappa = \tt\displaystyle \frac{2}{d_s} (\frac{P}{\pi}+\frac{\mu_s \cdot d_p}{\cos\alpha}) \) ・・・③
として、②式は
\( \tt \displaystyle \frac{\tau}{\sigma} =\kappa \)・・・④
と表記できるようにしておく。
ボルトの降伏の条件
さて、降伏の条件はせん断ひずみエネルギー説(Misesの降伏条件)がよく合うとされる。
せん断ひずみエネルギー説とは、σとτから算出される応力値 σeq が、材料の下降伏点もしくは0.2%耐力(σy)に達した時に降伏するという説。
引張応力\(\tt \sigma \)とせん断応力\( \tt \tau \)を使えば、その降伏条件の式は
\(\tt \sigma_{eq}=\sqrt{\sigma^2+3\tau^2} ≧ \sigma_y \)
この説をもとに、さらに締結の実験結果に整合させた研究があり、ボルトの降伏においてはせん断応力の係数3を1.8にしたものが、実用に合うとされる。
(せん断は表面的な発生であり、内部は弾性を保っている事を推論とする説 : 辻/丸山 精密工学会誌 59-4 。 ねじ締結の原理と設計” も理論値計算にこの式が使用されている)
つまり
\(\tt \sigma_{eq}=\sqrt{\sigma^2+1.8\tau^2} ≧ \sigma_y \)・・・⑤
σeq がこれを満たせば、ボルトは塑性域に入り、それ以内であれば弾性域内。
つまり、トルク法では設計の余裕度&締結のバラつきを踏まえ、σeqが σy に到達しないようなトルクの設定にすればよい。⑤式を変形しておく
\( \tt \displaystyle (\frac{\sigma}{\sigma_y})^2+ 1.8 \displaystyle (\frac{\tau}{\sigma_y})^2 ≧ 1 \) ・・・⑥
限界トルク算出
設定トルクを導くための締結のバラつき&設計の余裕度の要素は以下。
- 締結後にかかる外力負荷への降伏応力(σy)に対する余裕分:m x100(%)
- 残留軸トルク率(締結直後のねじり解放分を除いた残留軸力率) :λ x100(%)
- トルクレンチの誤差 :p(%)
- 摩擦係数 のバラつき
理論式への取り込みの詳細は”ねじ締結の原理と設計” が詳しい。大枠の流れだけ以下に。。
- ④式に残留軸トルク率λ%、⑥式に外力負荷への余裕度m%を組み込み、それらの式から(ボルトに最大にかけられる)限界応力σHを求める
- ④式へ残留トルク率λの取り込み:\( \tt \displaystyle \frac{\tau}{\sigma} =\lambda\kappa \)・・・⑦
- ⑥式に外力負荷への余裕度mの取り込み:\( \tt \displaystyle (\frac{\sigma}{\sigma_y}+m)^2+ 1.8 \displaystyle (\frac{\tau}{\sigma_y})^2 ≧ 1 ・・・⑧ \\[8pt] \)
- ⑦式を\( \tt \tau = \lambda \kappa \sigma\) として ⑧式に代入、限界軸力時の引張応力σ=σHとすれば、\( \\[12pt] \tt \displaystyle (\frac{\sigma_H}{\sigma_y}+m)^2+ 1.8\lambda^2\kappa^2 \displaystyle (\frac{\sigma_H}{\sigma_y})^2 = 1 \\[12pt] \)
- この二次方程式を解けば、
\( \\[8pt] \tt \displaystyle \frac{\sigma_H}{\sigma_y}=\tt \displaystyle \frac{-m+\sqrt{m^2-(m^2-1)(1+1.8\lambda^2\kappa^2)}}{1+1.8\lambda^2\kappa^2} \\[8pt] \)
右辺は全て定数(ねじ諸元、締結時の条件)のため
\( \xi=\tt \displaystyle \frac{-m+\sqrt{m^2-(m^2-1)(1+1.8\lambda^2\kappa^2)}}{1+1.8\lambda^2\kappa^2} \) と簡易表記すれば、
\( \\[8pt] \tt \displaystyle \frac{\sigma_H}{\sigma_y}=\xi \\[8pt] \) 、つまり、\( \\[8pt] \tt \sigma_H=\xi \cdot \sigma_y \)
- σHに有効断面積Asをかけ、ボルトの限界軸力FsHを算出
\(
\begin{align}
\tt F_{sH}&=A_s\cdot \sigma_H \\[8pt]
&=A_s\cdot\xi \cdot \sigma_y
\end{align}\\[8pt]
\) - 最小トルク係数Kminを用いて、この時の限界トルクTfHを算出
\( \\[8pt] \tt T_{fH}=K_{min}\cdot F_{sH}\cdot d \\[8pt] \) - トルクレンチ誤差p%を踏まえた、誤差下限トルクTfLを算出
\( \\[8pt] \tt T_{fL}=\displaystyle \frac{1-p/100}{1+p/100}\cdot T_{fH} \\[8pt] \) - TfL時の最小軸力FsL(最大トルク係数Kmax時)を算出
\( \\[8pt] \tt F_{fL}=\displaystyle \frac{1-p/100}{1+p/100}\cdot \frac{K_{min}}{K_{max}}\cdot F_{fH} \\[8pt] \)
締結時の目標トルク(限界トルク)は、 TfH と TfL の平均値 TfM で設定をする。
- TfM = (TfH + TfL) / 2
この理論式を組み込んで計算できるツールを以下に。
さて、例としてボルトの強度区分8.8を使用し、締結後にかかる外力負荷に対する余裕度を10%、締結後の残留トルクを75%、トルクレンチの誤差を±3% 、摩擦係数を折りこんで計算してみると以下
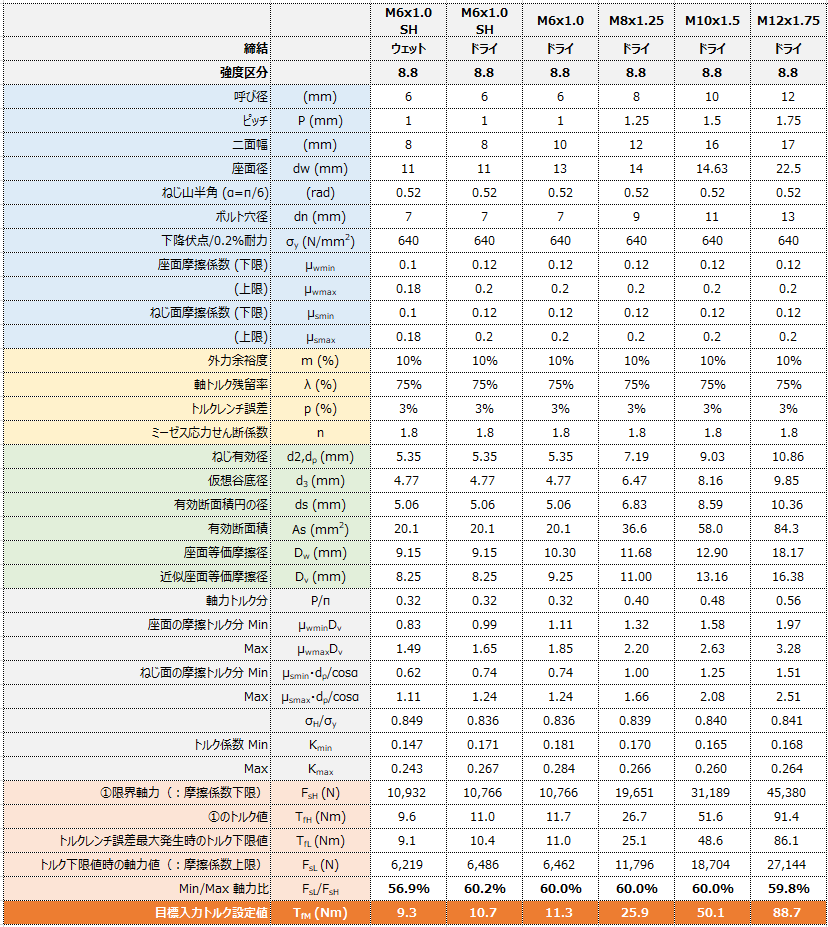
この計算結果から、ひとつ、、
結果から、弾性域内にて使用する時の目標トルクの目安は当然として、バラつきを折りこんだ発生軸力(理論値)も見て取れる。
というのも、バラつきによる最小/最大の軸力差が結構大きい事。
(表の下から二行目に発生軸力の最小/最大の比を記載)
たとえ同一トルクで締結しても、発生する軸力は40%近くバラつきが生じる。
つまり、これがトルク法の限界。
ちなみに、軸力のバラつきを抑えるには、塑性域での締結管理の方が有利
( <-> 締結する度にボルトが交換要となるため一長一短ではあるが・・・)
入力トルクの設定(えいや!で設定する時)
(もちろん、ある程度理論値の算出経緯を踏まえた上ではあるが、、)
いちいち計算せずとも、T-θ線図をベースに、えいやっ!で設定しても何とかなる。
以下にて、、
現品降伏点Ty-realを使用する場合
これは、該頭部位の締結から得られるT-θ線図を利用する。
T-θ線図で降伏点に入るトルク(Ty-real)を一度計測し(見極めてから)、その降伏点のトルクの65%を目途に目標トルクを設定してしまう方法である(70%程度ともいわれる)。
この現品降伏点Ty-realは、線図の傾きが 2/3・θに変化した点を使用する。
以下である
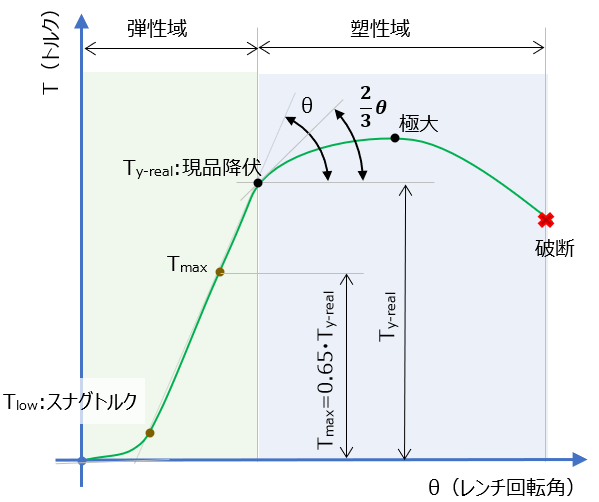
この65%は、理論値計算において降伏発生時のトルクに対する目標トルクがおおよそ65%前後で一定している事を利用している。
(”強度区分”の降伏点を使わず)実の材料の機械的性質における降伏点を利用できることから ( -> より高い降伏点の適用が期待できる)この設定方法は理論値より高めの目標トルクを設定値にできる事が多い。
つまり、高い軸力を想定した設計ができる。
また同じ目的にて、ボルトの持つ軸力の余裕度を小さくできる事を見極めた上で(残留軸トルクを上げる方法をとる(ナット側締結等/ウェット締結で摩擦係数を低減させる)等々により)、この65%を80%程度まで攻める事もある、、が、、
- トルクレンチのバラつき±3%、外力負荷への余裕度が10%、摩擦係数を大体±30%程度見込んだ理論値の上限が85%前後である事
を踏まえれば、80%以上は避けておいた方がよい。
よってちょっと余裕をもち、現品降伏トルクの65%~80%の間が設定の目安で、後から理論値計算をしたとしても、そこそこ成立するトルク設定値になっているはず(高すぎず、低すぎずのトルク値)
->70%程度が経験値(前述)
追記
ボルトを弾性域内で使用するトルクの設定方法の次は、ねじ山の破断について。
ボルトを弾性域ぎりぎりまで使える設定をしても、ねじ山自体が破損しては元も子もない。。
次の記事にて



