数学基礎テーマの覚書全般を横断するタグ（指数・対数、三角関数、ベクトル、級数などの基礎テーマの整理）
指数・対数 [指数] 指数で0乗が１になる理由
どんな数字ａでも0乗は常に”1”。これは、分母、分子に同じ数のａが並んで約分されて1になるため。これは、指数にマイナスがつく場合は逆数になっている事を知っているとすっとわかる。概要をなるべく簡単に説明。
その他 [実数] 実数の連続性：1=0.999・・って？
1= 0.9999・・・への理解は、同じ点を示しているが表示が違うだけと捉える。実数の世界では点は連続しているのである。ほぼ等しいのではなく、（極限では）等しいと理解する。この等式の両辺は”等しい”のである。
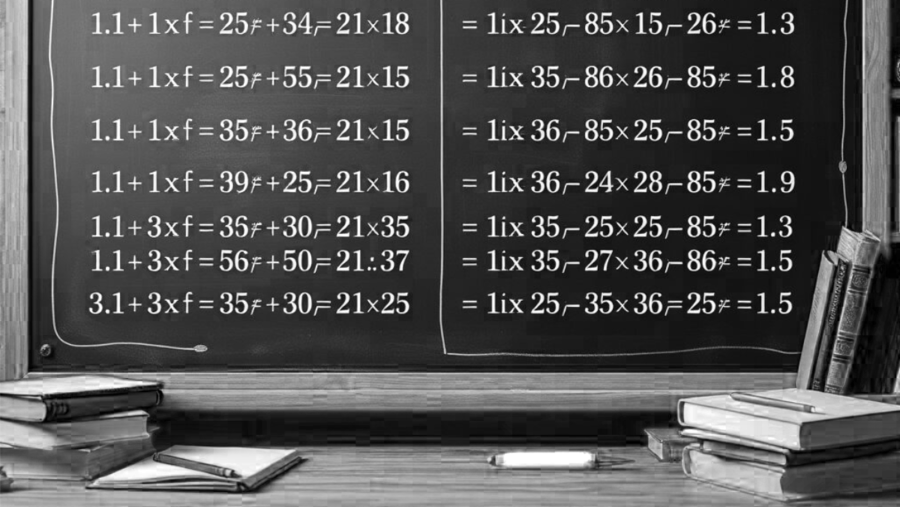行列 [行列]3.行列の積の計算： 行列の積は、”ベクトルの内積計算”の繰返し
はじめに前回の和と差、に続いて今回は、積について行列の積行列計算の積とされる計算 X = A・B は少し特殊。肝は、行列の積の計算にて算出される行列X の各成分は、行列Aの行ベクトルと行列Bの列ベクトルの内積値という事（ベクトル成分の内積計...
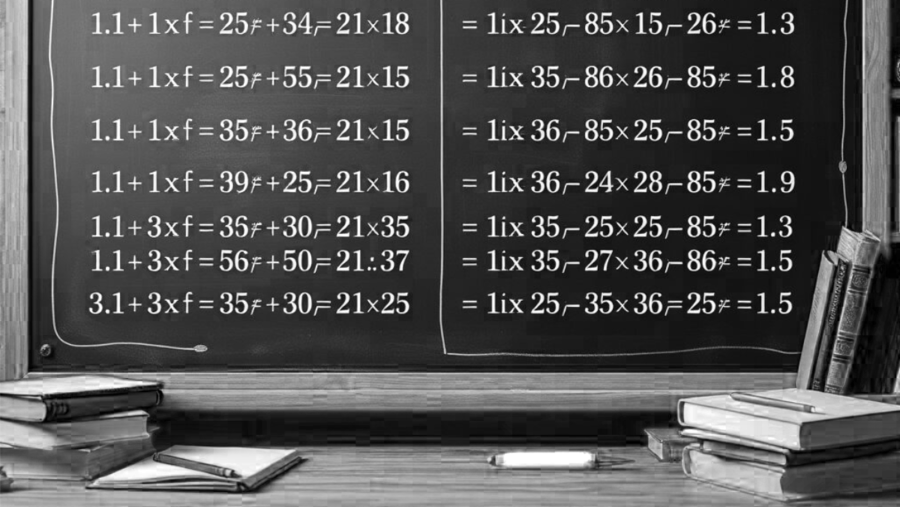行列 [行列]2. 行列の和と差の計算
行列計算における和と差とされる計算 C=A ± B は、それぞれの成分を足し算、引き算。
ベクトル [ベクトル]2. ベクトルの内積の意味とその計算
ベクトルの内積をまとめて簡易説明。内積の意味と定義から、成分計算の導き方、簡単な使い道まで。
ベクトル [ベクトル]1. ベクトルとは？から
ベクトルとは”大きさ”と”向き”を同時に持つ量、基本はこれだけだが、複数情報を一つの形で持つことができ、またそのままの形で計算可となるため、数学、物理にて多用される（ベクトル計算後に成分値算出等々）。
指数・対数 [対数] 対数の基本的な見方：対数のしくみと足し算、引き算について
対数も指数の特徴を踏まえれば特に新しい事はない。対数と指数の関係からその基本的な性質、ついでに対数の足し算＆引き算について、底の入れ替えについても
指数・対数 [指数] 小数をもつ指数の便利な見方 (10の乗数のとき)、対数もついでに
指数に小数点を含むべき乗数において、全ての実数の表現ができるのであるが、10のべき乗の指数が小数点を含む場合、整数部分はその数字の桁とリンクし、小数点以下は10進法での数字の並びとみれば、元の数字がだいたい見積れるようになる。
基礎関数・公式 [級数] 級数展開のとらえ方からはじめて、テイラーの定理 → テイラー展開 → マクローリン展開のつながりを順に
級数展開とは何かを基礎から解説。テイラーの定理を出発点に、テイラー展開・マクローリン展開の意味と違い、剰余項の考え方まで整理して覚書化