 指数・対数
指数・対数 [指数] 指数の四則計算のしくみ(たし算、ひき算、かけ算、わり算)と、小数点のついた指数の見方
指数が整数の時は抵抗がないのに、10の1/2乗(分数乗)、10の‐3乗(マイナス乗)となったとたんに”あれっ?”となる方へ。指数の見方&特徴の簡単な説明と、指数の計算(足し算、引き算、かけ算、わり算(分数))の中身について。意味がわかれば、結構簡単。例えば。。10の1/2乗は、2乗すると10になる数。(答えは√10)
 指数・対数
指数・対数 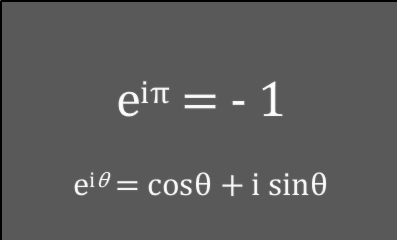 基礎関数・公式
基礎関数・公式 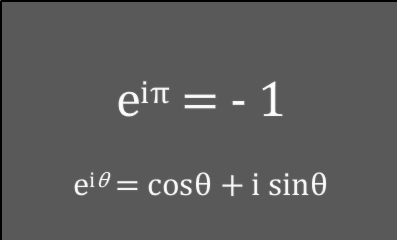 基礎関数・公式
基礎関数・公式  基礎関数・公式
基礎関数・公式  基礎関数・公式
基礎関数・公式  e:ネイピア数
e:ネイピア数  e:ネイピア数
e:ネイピア数  e:ネイピア数
e:ネイピア数  e:ネイピア数
e:ネイピア数