計算技術としてではなく数学を ”物事を整理し、構造として理解するために利用” する際の覚書群
基礎関数・公式 [級数] 級数展開のとらえ方からはじめて、テイラーの定理 → テイラー展開 → マクローリン展開のつながりを順に
級数展開とは何かを基礎から解説。テイラーの定理を出発点に、テイラー展開・マクローリン展開の意味と違い、剰余項の考え方まで整理して覚書化
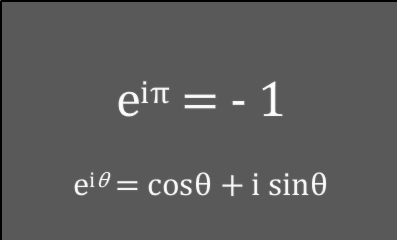基礎関数・公式 [オイラーの公式]2 : 世界で最も美しい公式の導き方
オイラーの公式は、基本、指数関数(e^θ) と 三角関数(sinθ、cosθ)の等式化であるが、ただこれを関連付ける時に、e^θ、sinθ、cosθ の各々3つが持つ一般的な性質を, マクローリン展開（級数展開）を利用して見事に組み合わせている。この成立過程も非常に美しい。このあたりの話を。。。
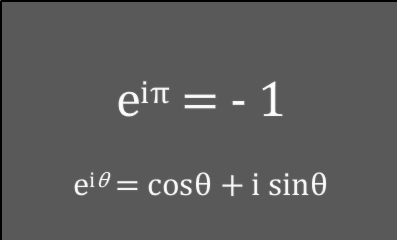基礎関数・公式 [オイラーの公式]1 : 世界で最も美しい公式の見かた、使いかた
世界で最も美しいといわれる式 e^(iπ)=-1 はオイラーの公式 e^(iθ)= cosθ + i sinθ から算出される。基礎から応用まで解説。指数関数・三角関数・複素平面を統合する仕組みを図とともに理解。
基礎関数・公式 [三角関数]2：sin と cos のたし算 と ひき算
はじめに\(sin x \) と \(cos x \)のたし算 / ひき算について。つまり、\( a \cdot cos x ± b \cdot sinx \) の型。この型は、\( \sqrt{a^2+b^2} \cdot cos(x ̠...
基礎関数・公式 [三角関数]1：加法定理はベクトルの内積計算と同じ
ベクトルの内積として三角関数の加法定理をみれば、そのしくみは簡単にわかる（図でも書いてみれば、そりゃそうか。。。の一発理解レベル）
e:ネイピア数 [e:ネイピア数]2：微分における ”\(e \)” の登場：対数の微分の中で見つかるネイピア数 ”\(e \) の定義” と それを使った対数/指数の微分への展開
対数 logₐx の微分を基礎から式展開で追い、底の変換公式とネイピア数 e が自然に現れる理由を解説。オイラーが発見した極限式、平均値定理による導出も併せて整理した覚書。
e:ネイピア数 [e:ネイピア数]1：ネイピア数 “e” とは何か？ 定義式から読み解く “e＝2.718…”の意味
“増えた分もまた増える”という複利のイメージと、ネイピア数 e の定義式をたどることで、その式が意味するところのひとつの見方を。e の値がなぜ出るのか、数学的な背景と直観的な理解をつなげる覚書。
座標・単位・実数・虚数 [単位] 角度”ラジアン”が便利な理由
日常の角度表示と違い（度数表示：90°とか360°とか）、数学、物理ではラジアン表示（π）が主に使用される。圧倒的に使い勝手が良いからである。ラジアン表記の意味と使い勝手の良いところを説明。ラジアンの値は、ｒ＝１の円(周長：2π)を、中心角Θで切り取った時の ”円弧の長さ” である。
座標・単位・実数・虚数 [極座標] 座標軸→ピタゴラスの定理→三角関数→極座標までの流れ
工学で使用される座標軸の定義と極座標の定義の話。極座標は定義を忘れないように、はじまりのピタゴラスの定理から三角関数の話、極座標の定義への利用までの流れまでの覚書