はじめに
”e =2.718281828・・・” (ネイピア数、自然対数の底)の定義は
\( e=\displaystyle \lim_{ n \to \infty } (1+\dfrac{1}{n})^{n} \) ・・・①
である。
円周率\(\pi \) であれば、「直径に対する円周の比」が \(\pi = 3.1415・・・ \) と説明すれば十分であり、直感的にも理解しやすい。。
しかし、この ”\(e \)” については、「一言でいうと何?」「そもそもこの定義式は何を意味している?」で、立ち止まってしまいがち。
一度仕組みを整理して、覚書化しておこうと。
\(e^x \) の定義式と複利計算の式からの \(e\)
先にのべれば、\(e^x \) は
\(e^x =\displaystyle \lim_{ n \to \infty } (1+\dfrac{x}{n})^{n} \) ・・・②
で定義される。
これは、複利計算の式
\(S_{n} =a \cdot (1 + \dfrac{r}{n})^n \) ・・・③ ( 初期値 \(a\) 、 利率 \(r\times 100 \)(%)、期間T内の清算回数 \(n \) )
において、 \(n → ∞\)、 かつ \( a=1 \) としたものに一致する。
特に、
| ②式が \(x=1 \) のときは、 |
| \( e=\displaystyle \lim_{ n \to \infty } (1+\dfrac{1}{n})^{n} \) ・・・④ |
| ②式が \(x=-1 \) のときは、 |
| \( \dfrac{1}{e}=\displaystyle \lim_{ n \to \infty } (1-\dfrac{1}{n})^{n} \) ・・・⑤ |
である。
e の直感的な意味
複利計算の観点からみれば、\(e \) は次のように解釈できる。
\(e \) のとらえ方
- 初期値を ”1”として、期間 T の間に「100%の増加率」が連続的に作用する環境を考える(期間 T で2倍)
- このとき、値は常に増加し、増加した分もその増加に組み込まれながら全体が増加する仕組み
この結果、期間 T 後の値は単純に2倍ではなく、\(e = 2.71828・・・\) 倍になる 。つまり
- \(e \)は 、「連続的に増加が組み込まれる状況における実効的な増加倍率」
を表す。同様に
- \(\dfrac{1}{e} \) は、連続的な減少が作用する場合の実効的な減少倍率を表す。
と見ることができる。
③式の複利計算の式の構造がわかれば、 \(e^x\) の定義式の意味するところのイメージがしやすくなる。
また、これから \(e\) のイメージもつかみやすくなるのだが、実際のところ複利計算の③式の意味するところ(仕組み)も、ちょっととっつきにくい
→ ”1+1/n” を ”n乗” したものが、なんで複利計算の式になるのかと
といったわけで、まずは、複利計算の式の仕組み(構造)から。
まずは、シンプルな単利計算からはじめてみる。
(→ 複利計算式の仕組みが大丈夫であれば、一気にとばして”e の定義式”へ)
単利計算の式
清算回数:期間中1回清算
ここは簡単。満期額の計算は、
満期金額=元金+利子=元金+(利率x元金)
=元金・(1+利率)
元金を\(a \)、利率を \(r\times 100 \)(%)、利率の期間を\(T\)、期間 \(T\) 後の満期金額を \(S_{1(1)} \) とすれば、
\(S_{1(1)} = a + a \cdot r= a \cdot (1 + r) \) ・・・⑥
図にかけば、こんな感じ(当然、とてもシンプル)

当たり前だが、元金 \(a \) に \( (1 + r)\) を掛ければ 満期額 \(S_{1(1)} \) 。別の見方をすれば、\( (1 + r) \) は、元金 \(a \) に対する実効増加率。
(<-複利計算はこの構造の繰り返し(同じ構造の式が組み込まれていく)、それが \(e \) の意味の理解につながるので一応。。。)。
複利計算の式
さて、複利計算へ。
清算回数:期間中2回清算
同じ利率 \(r\times 100 \)(%)で期間 \(T\) も同じ。
ただし、半分の \(\dfrac{1}{2} \)T の期間経過時に、一度利子を清算 (預金額: \(S_{2(1)}\) )
次の期間はこの利子を加えた額 \(S_{2(1)}\) を加え、元金を増やして再度預金、満期時(期間\(T\) 経過時)に清算。
この満期時の預金額 \(S_{2(2)} \) を以下で計算する(複利計算)。
さて、一回目の清算時の預金額は同じ式構成だが、期間は \(\dfrac{1}{2} \)T 分となるため 利子は \( a\times \dfrac{r}{2} \)
よって、
\(S_{2(1)}= a (1 + \dfrac{r}{2})\) ・・・⑦ ← これが二回目の期間の元金。
満期時の預金額\(S_{2(2)} \) は⑦が元金となるので、それに利子をかけたものを足して、
\(\begin{align}
S_{2(2)} &= a \cdot (1 + \dfrac{r}{2})+ a \cdot (1 + \dfrac{r}{2}) ・\dfrac{r}{2} \\[6pt]
&= a \cdot (1 + \dfrac{r}{2})^2 ・・・⑧
\end{align} \)
これは、式を見るより、図で見た方が構造はわかりやすい。図に描くとこんな感じ
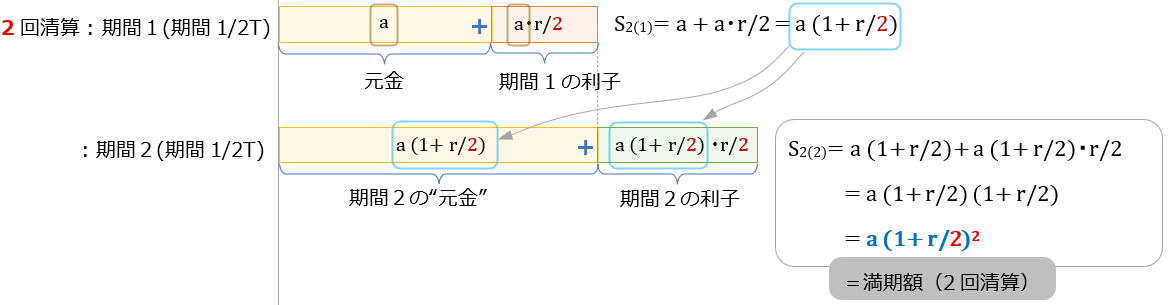
単利の時と同様④式の \( (1 + \dfrac{r}{2})^2 \) の部分は実効増加率、つまり、元金\(a \)に対して何倍になるかの係数。
(\( S_{2(2)} = a \times (実増加率) \)) ← この構造は1回清算の時と同じ
清算回数:期間中3回清算
流れをもう少しはっきりさせるために、期間中清算を3回した場合も図にかいておく。
満期時の預金額は、
\(S_{3(3)}\) は、\(S_{3(3)} =a \cdot (1 + \dfrac{r}{3})^3 \) ・・・⑨
となる。
各清算回毎の式を、図に描けばこんな感じ 。
→ \( (1 + \dfrac{r}{3})^3 \) が組み込まれていく様子がわかる。
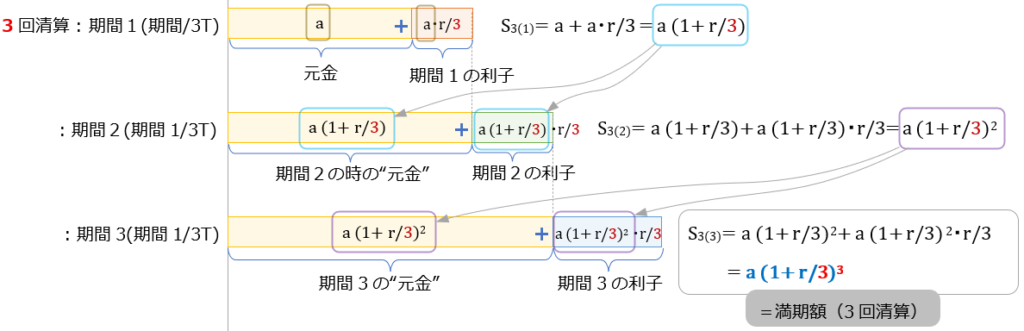
今までの計算と同様に、⑨式の \( (1 + \dfrac{r}{3})^3 \) の部分は、元金\(a \)に対して何倍になるか?の実効増加率を示す係数
( \( S_{3(3)} = a \times (実効増加率) \)) ← この構造は2回清算の時と同じ
清算回数:期間中n回清算(一般化)
さて、清算回数がn回になった場合を計算してみる
きちんと証明しても良いが、上と同じように \( (1 + \dfrac{r}{n}) \) が組み込まれていくだけなので、ここでは以下の図で十分。
組み込まれる様子見ながら、満期時の預金額 \(S_{n(n)} \) をみれば、
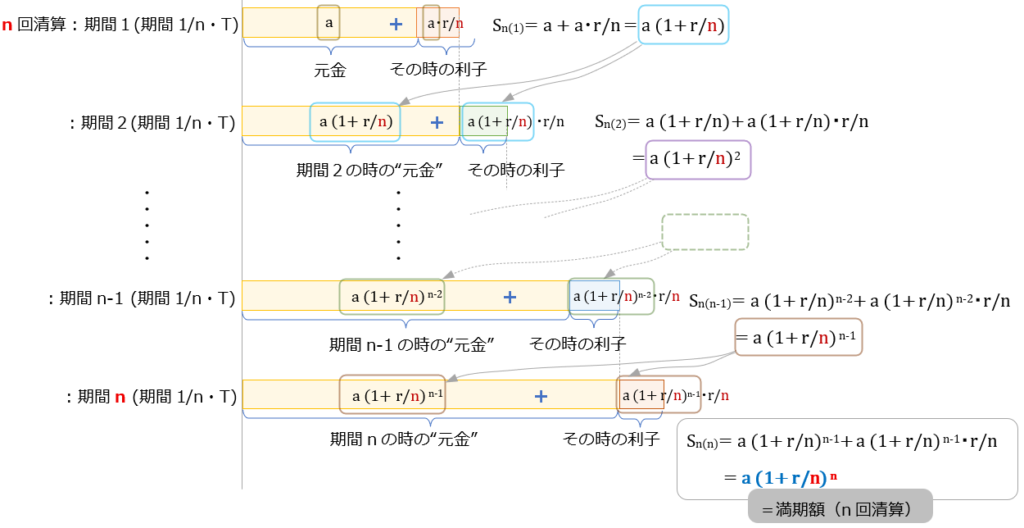
この図から満期時の預金額は、
\(S_{n(n)} =a \cdot (1 + \dfrac{r}{n})^n \) ・・・⑩
ここでも、この⑩式の \( (1 + \dfrac{r}{n})^n \) は、元金\(a \) が満期時に何倍になるかの”実効増加率” になっている
( \( S_{n(n)} = a \times (実増加率) \) ) ← この構造は同じまま
以上が、利子が元金が組み込まれていく時の式の仕組み(構造)
清算回数:期間中に∞回清算(極限 n→∞)
さて、⑩式をつかって清算回数を無限大にすれば、単純に
\(S_∞ =\displaystyle \lim_{ n \to \infty } a \cdot (1 + \dfrac{r}{n})^n \) ・・・⑪
( \( S_∞ = a \times (実効増加率) \) ) ← 結局、最後までこの構造は変わらない
結局、( \({\color{green}{1}} + \dfrac{r}{n}\) ) は、” その清算回の元本率(\(\color{green}{1}\)) ” + ” \(\color{blue}{n}\) 回清算時の一回当たりの利率 (\(\dfrac{r}{\color{blue}{n}}\)) ” であり、とどのつまりが、清算一回当たりの元本の増加率。
ある回の清算時の預金額は、(前の回までに増えた)元本に”同率”の ( \({\color{green}{1}} + \dfrac{r}{n}\) ) をかければ、その回の預金額が算出される構造。
( \( \underbrace{S_(x)}_{x回清算時の預金額} =(\underbrace{a \cdot ( 1 + \dfrac{r}{n})^{x-1} }_{前の回((x-1)回目)からの元本}) \cdot (\underbrace{1 + \dfrac{r}{n}}_{一回当たりの増加率}) \))
満期の時は、この掛け算を \(\color{red}{n}\) 回繰り返す事になるため、実増加率は単純にこれを(\(\color{red}{n}\)乗) すればよい。つまり、実増加率は、 ( \(1 + \dfrac{r}{n})^ {\color{red}{n}} \)
これがこの式のしくみ( 初期値(元金)の \(a \) を掛ければ満期時の預金額が算出される)
で、この清算回数の \(n\) を無限大にとばしたのが⑦式
e の定義式
さて、既に \(e \) の定義式は既にみえてはいるが、一応。
⑪式にて
- 元金 \(a =1 \)
- 利率 \(r=1\) (100%:期間Tで2倍)
とすれば、 \(e \) の式。
つまり、⑪式の満期時の預金額 \(S_{\infty}\) から確認してみれば、
\(S_{\infty}=\displaystyle \lim_{ n \to \infty } (1+\dfrac{1}{n})^{n} =e \) ・・・⑫
であり、”\(e \) ”の定義式と一致
\(e \) は、「複利計算の極限(連続複利)」の限定版として現れる値とおなじ
また、実際の値を計算すれば、\(S_{\infty}=e = 2.71828・・・ \) である。(⑫式が収束する事、値の算出はまた別途)。
以上が、”\(e \) ”の定義式からの意味の解釈
補足:\(e \) の定義式内では、同じ ”1” であるが故に ”初期値” と ”利率” は見えにくくなっているが、
\( \begin{align}
e &=\displaystyle \lim_{ n \to \infty } (1+\dfrac{1}{n})^{n} \\[6pt]
&= 1(:初期値) \times \displaystyle \lim_{ n \to \infty }(1+\dfrac{1(:利率)}{n})^{n}
\end{align}\)
を各々意味している。← 同じ”1”でも別の意味
まとめ
式 からの解釈にて、\(e\) とは、
- 初期値 ”1”、期間 T で2倍にふやす増加力が常時作用する環境下(率:100%)
- このとき値は常に増加し、増加した分もその増加に組み込まれながら全体が増加する仕組み
であるときの、実効増加率で、値は \(e = 2.71828・・・\)、 と見ることができる ← \(e\) のひとつの意味。
単純例:100万円を年利100%(一年(期間T)で2倍)で運用したとすると、単利(一回清算)だと一年後に200万円。
同じ年利でも頑張って毎日毎時間毎秒でも清算し続け増えた利子分をどんどん元金に組み込んでいけば、一年後には倍の200万円ではなく、約271.8万円(=100万円x\(e \) )に近い額まで届くって話。
これで捉えておくと、”\(e \) ” も少し身近。
注記
肝は、増加した分が、次の増加に組み込まれ続ける構造をもっているということ。
この
” \(a \cdot (1 + \dfrac{r}{n})^n \) ”
という形がその本体であり、\(e \) は利率100% (r=1)、初期値1(a=1)の限定条件下での極限値である。
→ ここを抑えれば、”\(e \) ” の定義式は単に複利計算の限定版(利率100%、初期値1)。なんて事なし
ちなみに、こうしてみると見ると、色々なトコロで”e”が出てくるのは、結構自然に思えてくる(イメージしやすくなる)。
(一年したら急に倍になるっていうより、徐々に増加していく方が普通、増えた分も次の増加に組み込まれて寄与していくのも普通。。。)
補足(\(e^x \) の解釈)
\(e^x =\displaystyle \lim_{ n \to \infty } (1+\dfrac{x}{n})^{n} \)・・・②
であるが、上述の⑫式 \(S_∞ =\displaystyle \lim_{ n \to \infty } a \cdot (1 + \dfrac{r}{n})^n \) と比較すれば、関数 \(e^x \) の ”\( x \) ” はその環境下での増加力として働き(⑦式での利率”\( r\) ”)、\(e^x \) は、増加力が変化していく時の出力値であるとみる事ができる。
\(e^x \) の導入ついてはこちら
ついでに ”\( x \) ” の増加にともなう関数 \(e^x \) の見方として、たとえば \( x =1、2 \) を例にとれば、
- \( x =1 \) : \(e^{\color{red}{1}}\)
→ <解釈> 期間Tで2倍になる一定の増加力( \(\color{red}{1} \) = 100%(利率)) がかかる環境下では、期間T経過時の実増加率は約2.718倍 (= \(e^1 \)) になる - \( x =2 \) : \(e^{\color{red}{2}}\)
→ <解釈> 期間Tで3倍になる一定の増加力( \(\color{red}{2} \) = 200%(利率)) がかかる環境下では、期間T経過時の実増加率は約7.389倍 (= \(e^2 \)) になる - ・・・
といった見方も可。
(\( x \) が時間tで表してある関数といった例 ( \(e^{αt}\))であれば、時間tの経過に伴い ”増加力(利率)自体が増える環境下” での関数、とイメージするのもいける)
語呂合わせ
最後に、”\(e \)” の値の覚え方の語呂合わせ
e =2.71828182845904523536・・・
(フナ一鉢二鉢しごく押し目にさめ山麓:め=5)

